LeetCode-094-二叉树的中序遍历

最新推荐文章于 2024-01-13 16:03:18 发布

原创最新推荐文章于 2024-01-13 16:03:18 发布 · 158 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#leetcode

力扣专栏收录该内容

94 篇文章

订阅专栏

本文详细介绍了二叉树的前序、中序、后序遍历的递归与非递归方法，包括代码实现，并给出了层次遍历的解决方案。通过对不同遍历方式的解析，帮助读者深入理解二叉树操作。

LeetCode-094-二叉树的中序遍历

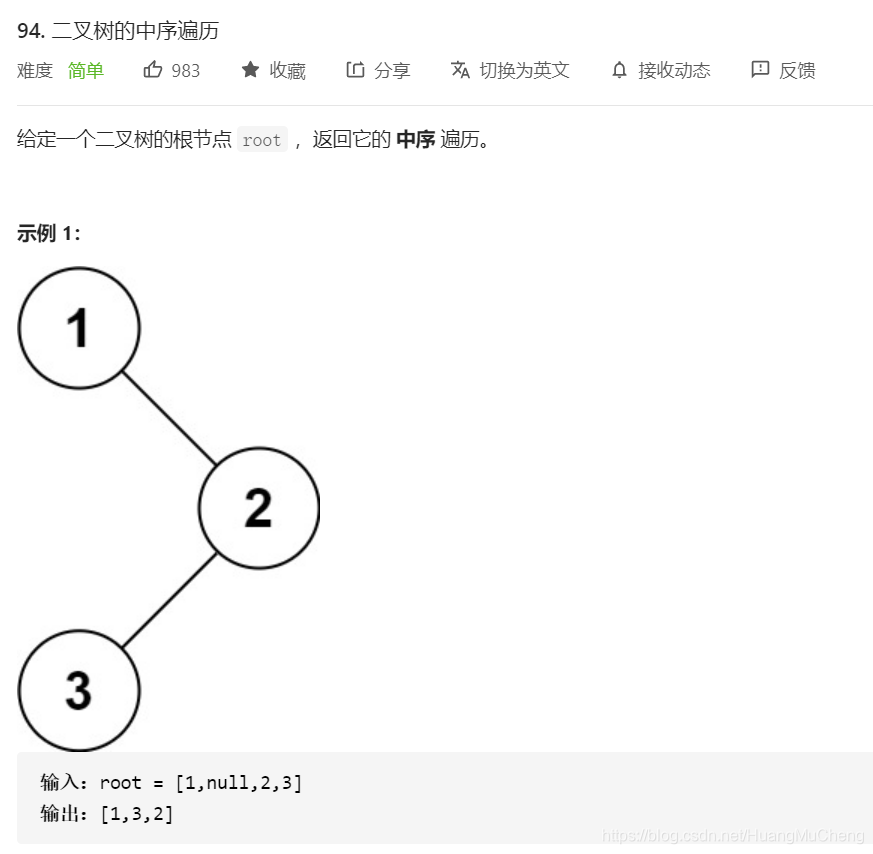
在这里插入图片描述

思路

参考迭代解法，时间复杂度 O(n)，空间复杂度 O(n) - 二叉树的后序遍历 - 力扣（LeetCode） (leetcode-cn.com)

二叉树有三种常用的遍历方式，分别为先（根 -> 左 -> 右），中（左 ->根-> 右），后（左 ->右-> 根）
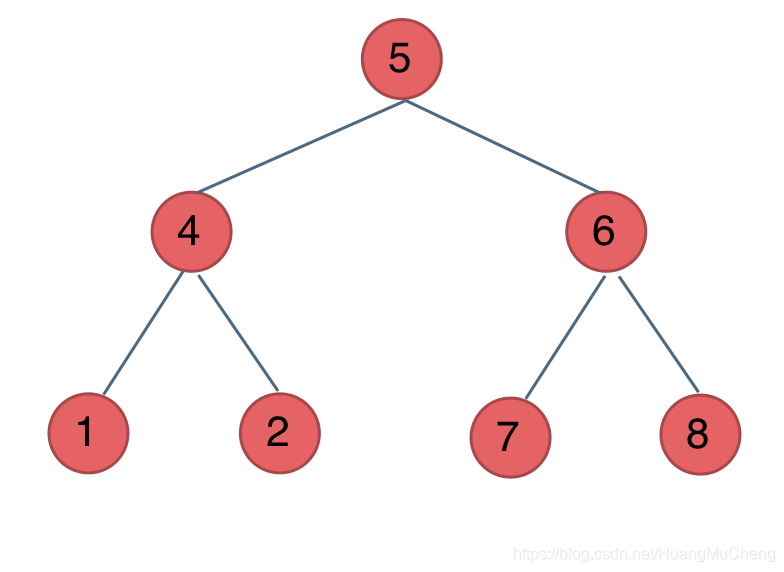
在这里插入图片描述
前中后序遍历顺序如下：

前序遍历（中左右）：5 4 1 2 6 7 8
中序遍历（左中右）：1 4 2 5 7 6 8
后序遍历（左右中）：1 2 4 7 8 6 5

这里顺便总结一下二叉树的三种遍历的递归和非递归写法
参考：

帮你对二叉树不再迷茫，彻底吃透前中后序递归法（递归三部曲）和迭代法（不统一写法与统一写法） - 二叉树的后序遍历 - 力扣（LeetCode） (leetcode-cn.com)

迭代解法，时间复杂度 O(n)，空间复杂度 O(n) - 二叉树的后序遍历 - 力扣（LeetCode） (leetcode-cn.com)

1.递归：

1.1先序遍历

void dfs(TreeNode root) {
    visit(root);
    dfs(root.left);
    dfs(root.right);
}

1.2中序遍历

void dfs(TreeNode root) {
    dfs(root.left);
    visit(root);
    dfs(root.right);
}

1.3 后序遍历

void dfs(TreeNode root) {
    dfs(root.left);
    dfs(root.right);
    visit(root);
}

2.非递归

2.1先序遍历

public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> res=new ArrayList<>();
        Stack<TreeNode> stack=new Stack<>();
        while(!stack.isEmpty() || root!=null){
            if(root!=null){
                res.add(root.val);
                stack.push(root.right);
                root = root.left;
            }
            else {
                root = stack.pop();
            }
        }
        return res;
    }

2.2中序遍历

public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> res=new ArrayList<>();
        if(root==null)return res;
        Stack<TreeNode> stack=new Stack<>();
        while(!stack.isEmpty()||root!=null){
            if(root!=null){
                stack.push(root);
                root=root.left;
            }
            else {
                root=stack.pop();
                res.add(root.val);
                root=root.right;
            }
        }
        return res;
    }

2.3后序遍历

public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> res=new ArrayList<>();
        Stack<TreeNode> stack=new Stack<>();
        while(!stack.isEmpty() || root!=null){
            if(root!=null){
                res.add(0,root.val);//头插，使得中左右->右左中
                //先左后右，使得右左中->左右中
                stack.push(root.left);
                root = root.right;
            }
            else {
                root = stack.pop();
            }
        }
        return res;
    }

3.层次遍历

public List<List<Integer>> levelOrder(TreeNode root) {
        List<List<Integer>> ans=new ArrayList<>();
        if(root==null) return ans;
        
        Queue<TreeNode> queue=new LinkedList<>();
        queue.add(root);
        while(!queue.isEmpty()){
            int n=queue.size();
            List<Integer> list=new ArrayList<>();
            while(n>0){
                TreeNode node=queue.poll();
                list.add(node.val);
                if(node.left!=null)queue.add(node.left);
                if(node.right!=null)queue.add(node.right);
                n--;
            }
            ans.add(list);
        }
        return ans;
    }