LeetCode-062-不同路径

最新推荐文章于 2025-10-12 17:25:59 发布

原创最新推荐文章于 2025-10-12 17:25:59 发布 · 86 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#leetcode

力扣专栏收录该内容

94 篇文章

订阅专栏

本文介绍了解决LeetCode题目062不同路径的两种方法：排列组合及动态规划。排列组合方法通过计算从起点到终点的所有可能路径数；动态规划则通过构建二维数组逐步计算出所有路径数。

LeetCode-062-不同路径

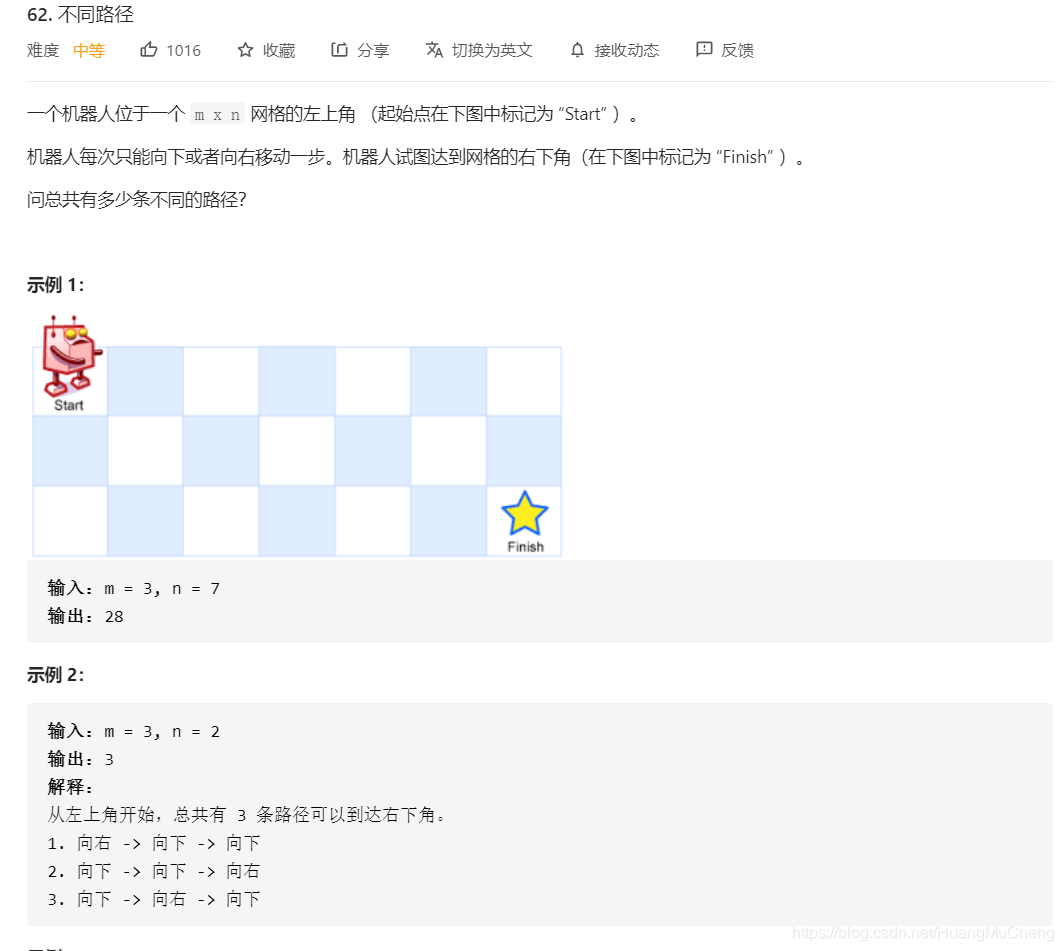
在这里插入图片描述

思路

排列组合：
直接使用排列组合进行计算即可，需要m-1次向下和n-1次向右，共m+n-2次，所以只需在m+n-2次选择m-1次向右即可,即C(m-1，m+n-2)

动态规划：
dp[i][j]=dp[i-1][j]+dp[i][j-1]

代码

//排列组合
class Solution {
    public int uniquePaths(int m, int n) {
        long ans=1;
        for(int x=n,y=1;y<m;x++,y++){
            ans=ans*x/y;//注意，此处必须用ans=ans*x/y而不是ans*=x/y，否则无法整除
        }
        return (int)ans;
    }
}
//动态规划
class Solution {
    public int uniquePaths(int m, int n) {
        int[][] dp=new int[m][n];
        for(int i=0;i<n;i++){
            dp[0][i]=1;
        }
        for(int i=0;i<m;i++){
            dp[i][0]=1;
        }
        for(int i=1;i<m;i++){
            for(int j=1;j<n;j++){
                    dp[i][j]=dp[i-1][j]+dp[i][j-1];
            }
        }
        return dp[m-1][n-1];
    }
}