关于背包问题

最新推荐文章于 2025-12-12 15:43:51 发布

原创最新推荐文章于 2025-12-12 15:43:51 发布 · 133 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#动态规划 #算法 #leetcode

动态规划专栏收录该内容

10 篇文章

订阅专栏

这篇博客探讨了如何使用二维和一维动态规划（DP）数组来解决01背包问题。首先，介绍了二维DP数组的初始化和遍历过程，然后展示了详细代码。接着，解释了一维DP数组的实现，包括其定义、递推公式、初始化和遍历顺序，并给出了相应的代码实现。最后，提供了两种不同实现方式的完整算法流程。

二维dp数组 01背包问题

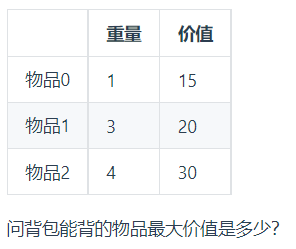
在这里插入图片描述

dp数组进行初始化

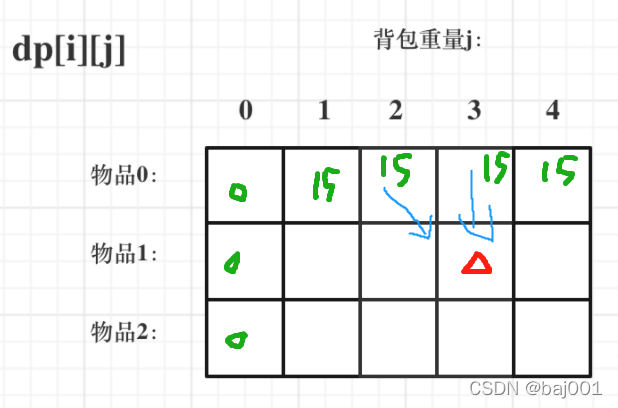
先遍历背包还是先遍历物品都是可以的

// weight数组的大小 就是物品个数
for(int i = 1; i < weight.size(); i++) { // 遍历物品
    for(int j = 0; j <= bagweight; j++) { // 遍历背包容量
        if (j < weight[i]) dp[i][j] = dp[i - 1][j]; 
        else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);

    }
}

详细代码如下

 public static void main(string[] args) {
        int[] weight = {1, 3, 4};
        int[] value = {15, 20, 30};
        int bagsize = 4;
        testweightbagproblem(weight, value, bagsize);
    }

    public static void testweightbagproblem(int[] weight, int[] value, int bagsize){
        int wlen = weight.length, value0 = 0;
        //定义dp数组：dp[i][j]表示背包容量为j时，前i个物品能获得的最大价值
        int[][] dp = new int[wlen + 1][bagsize + 1];
        //初始化：背包容量为0时，能获得的价值都为0
        for (int i = 0; i <= wlen; i++){
            dp[i][0] = value0;
        }
        //遍历顺序：先遍历物品，再遍历背包容量
        for (int i = 1; i <= wlen; i++){
            for (int j = 1; j <= bagsize; j++){
                if (j < weight[i - 1]){
                    dp[i][j] = dp[i - 1][j];
                }else{
                    dp[i][j] = math.max(dp[i - 1][j], dp[i - 1][j - weight[i - 1]] + value[i - 1]);
                }
            }
        }
        //打印dp数组
        for (int i = 0; i <= wlen; i++){
            for (int j = 0; j <= bagsize; j++){
                system.out.print(dp[i][j] + " ");
            }
            system.out.print("\n");
        }
    }

一维dp 数组（滚动数组）

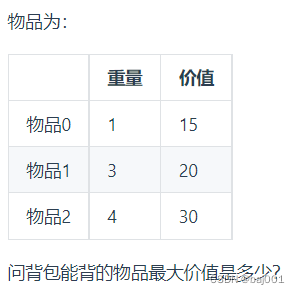
在这里插入图片描述

1、确定dp数组的定义

在一维dp数组中，dp[ j ] 表示：容量为 j 的背包，所背的物品价值可以最大为 dp[ j ]

2、一维dp数组的递推公式

dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);

其中，分别为不放 i 和放 i

不放i 的时候，包里的物品价值仍然为 dp[ j ]
放 i 的时候，为 预留出放i 的位置后，还能放物品的最大价值 + i 的价值

3、初始化 dp数组

容量为 j 的背包，所背的物品价值可以最大为dp[ j ]，那么dp[0]就应该是0，因为背包容量为0所背的物品的最大价值就是0

4、一维dp数组遍历顺序

for(int i = 0; i < weight.size(); i++) { // 遍历物品
    for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量
        dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);

    }
}

在这里插入图片描述
算法流程

    public static void main(String[] args) {
        int[] weight = {1, 3, 4};
        int[] value = {15, 20, 30};
        int bagWight = 4;
        testWeightBagProblem(weight, value, bagWight);
    }

    public static void testWeightBagProblem(int[] weight, int[] value, int bagWeight){
        int wLen = weight.length;
        //定义dp数组：dp[j]表示背包容量为j时，能获得的最大价值
        int[] dp = new int[bagWeight + 1];
        //遍历顺序：先遍历物品，再遍历背包容量
        for (int i = 0; i < wLen; i++){
            for (int j = bagWeight; j >= weight[i]; j--){
                dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]);
            }
        }
        //打印dp数组
        for (int j = 0; j <= bagWeight; j++){
            System.out.print(dp[j] + " ");
        }
    }