两百万人等着极越“趴窝”，夏一平却更开心了

作者｜王彬

封面｜极越直播截图

01｜极越的春晚

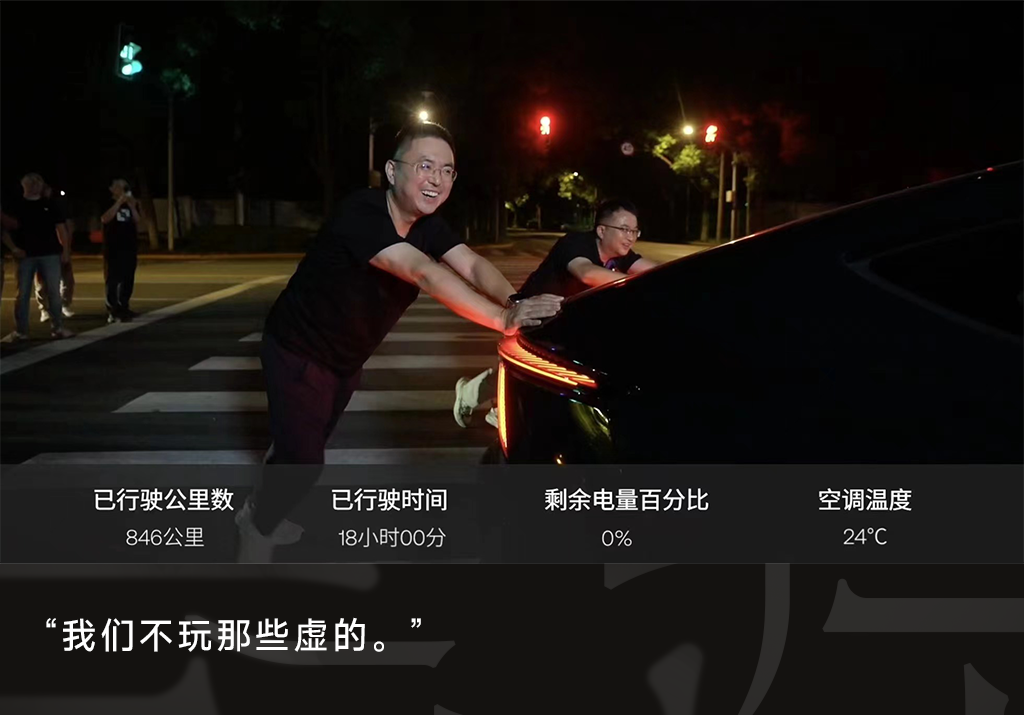
9 月 28 日凌晨 2 点，一台载满三人、不间断行驶了 18 小时的极越 07 终于耗光了电量，在上海嘉定郊区的一条马路上停了下来。

车上坐着的包括极越 CEO 夏一平在内的三名极越汽车高管爆发出剧烈的欢呼声，工作人员围了上来，大家都在说着“没想到”——一台 CLTC 续航里程为 880 公里的电动轿车，最终跑了 846 公里，续航达成率 96.14%。他们原本只打算跑 15 个小时，预估里程只有 800 公里。

直播中，极越 07 实际续航里程为 846 公里

手机屏幕前观看直播的无数观众、极越车主、员工乃至合作伙伴开始在弹幕中齐刷刷地表达自豪。一位极越员工说，当天是工作日，白天没有时间跟着直播。晚上 11 点下班回到家，她原本只想着打开 CEO 的直播看一眼，没想到一直看了两个多小时。最终续航定格在 846 公里的时候，他们整个公司都沸腾了。甚至两天之后，她在公司电梯间里还能听到同事在讨论那场直播。

在竞争激烈的中国汽车市场，极越并不是一个销量足够亮眼的品牌。时至今日，他们在卖车时还要不断向用户解释，极越到底是什么牌子。夏一平在直播中也不断重复，极越是百度和吉利联合打造。

大概是去年的这个时候，他们发布了第一款车，表现不佳。公司员工们大多吊着一口气，想要证明自己。过去几个月极越的销量从年初的 100 来台增长至 2000 余台，算是阶段性地稳住了脚步。

9 月 10 日他们发布了第二款车极越 07。48 小时后，他们宣布订单量突破 5000 台，过去他们从未达到过这一数字。一些员工在对外沟通时更有底气了。过去半年网络上不断有人揶揄他们，骂他们的车子不好，还到处碰瓷。现在销量起来了，至少能挺直腰板说话了。

但这个凌晨，或许才是这家创业公司过去一年积压情绪的释放口。车子终于停下来的那一刻，音响还在放着歌曲《难忘今宵》。夏一平和同事开始推车，一开始是慢慢推，后来跑了起来。园区门口的两个减速带，他们发力，一口气推了过去。

“那天晚上就像是我们极越的春晚，”上述极越员工说，“从来没有感受到公司的凝聚力这么强。”

夏一平可能是在场人员中最高兴的那个人。他满脸笑容，看起来毫无倦意。他在这台车上待了整整 18 个小时，喝了四杯咖啡和一罐红牛，是整场直播中唯一没有下车休息过的人。

“极越牛 X。”现场有人在直播结尾时喊道。夏一平愣了一下，笑了。“谢谢大家！”他说。

夏一平可能是当晚最高兴的那个人

02｜超出计划的 18 小时直播

9 月 27 日早上 8 点，上海嘉定 Robobase，一台极光绿配色的长续航版极越 07 停放在办公楼前。

这是极越汽车的上海总部。他们将要进行一场长达 15 小时的续航直播测试——这是他们计划中的直播时间，但实际上他们这趟行程最终耗时 18 小时，比他们预想中要多得多。

极越 07 的长续航版搭载了一块 100kWh 的宁德时代三元锂电池，CLTC 续航里程 880 公里。他们为续航测试规划了一条复杂的路线，路程是一个环线，从极越嘉定 Robobase 开始，到上海浦东国际机场，绕到苏州，再回到嘉定 Robobase。

极越 07 续航直播路线图

过去也常有车企 CEO 们下场做续航直播测试，但少有这样时长达十几小时，测试路段涵盖高速、城市高架、城区道路以及早晚高峰拥堵路段的。

在车上待满 18 个小时也不是一件轻松的事儿。它是一次对人的身体、精神乃至膀胱的持久考验。在直播开始之前，极越的员工给夏一平提建议，他可以在直播开始时出现一次，最后到车子电量快要耗尽时再过来。夏一平不同意，“不行，要干就要全程，（做假）没有意义。”

他为了这场直播做了诸多准备。直播的前一天，他专门拍了一条短视频分享自己的补给包，包括饼干、凤爪、红牛、游戏手柄、卡拉 OK 麦克风以及一大包成人纸尿裤——极越的员工担心 CEO 路程中可能没有时间上厕所。

早上 8 点 08 分，夏一平驾驶着极越 07 开始直播。此时正值上海早高峰时间，路程拥堵。直播间中的一些用户质疑，旁边骑自行车的人都比车子开得快。夏一平说，这就是早高峰啊，这就是大家上班最真实的行驶场景——别说骑自行车了，旁边走路的人都要比路上的车子快。上了高速，他们的速度升到 100km/h。这下没人再说他们车子跑得慢了。

过去市场上也常有一些续航测试，不管是车企自行组织的还是第三方汽车媒体的横评。但夏一平觉得很多测试都不太符合用户真实的用车场景，比如不少测试只跑高速，车速固定。有的没开空调，或者开了又偷偷关掉，甚至连车上的娱乐设施都不敢用。

他们这次直播没有打算玩那些“虚的”。全程空调开启，车上全程坐着三个人，接替开车，一路不停。甚至吃饭也在车上解决，目的就是为了还原用户最真实的用车场景。

副驾驶坐着的是极越整车产品负责人贾秀江。他在直播中负责解答用户疑问、介绍极越的产品理念。比如大家经常用电耗来比较车子，但如果没考虑车身重量，这样的对比也不科学。比如极越取消了换挡、打灯，但通过整车智能这些功能都可以自动实现，实际上他们开车的前几个小时中就没有手动操作过。长期快充有没有影响，要不要和慢充接替进行？现在电池技术发达了，不需要有这种担忧。

直播进行了两个小时，他们在车里唱起歌来，周杰伦的、邓紫棋的。贾秀江还演示了极越 07 的车载游戏——他们的合作方也在看着直播，强烈要求贾在直播中展示一下他们的游戏。高速路上，夏一平开着车，贾秀江在副驾屏幕上打开一款飞机小游戏，互不影响。

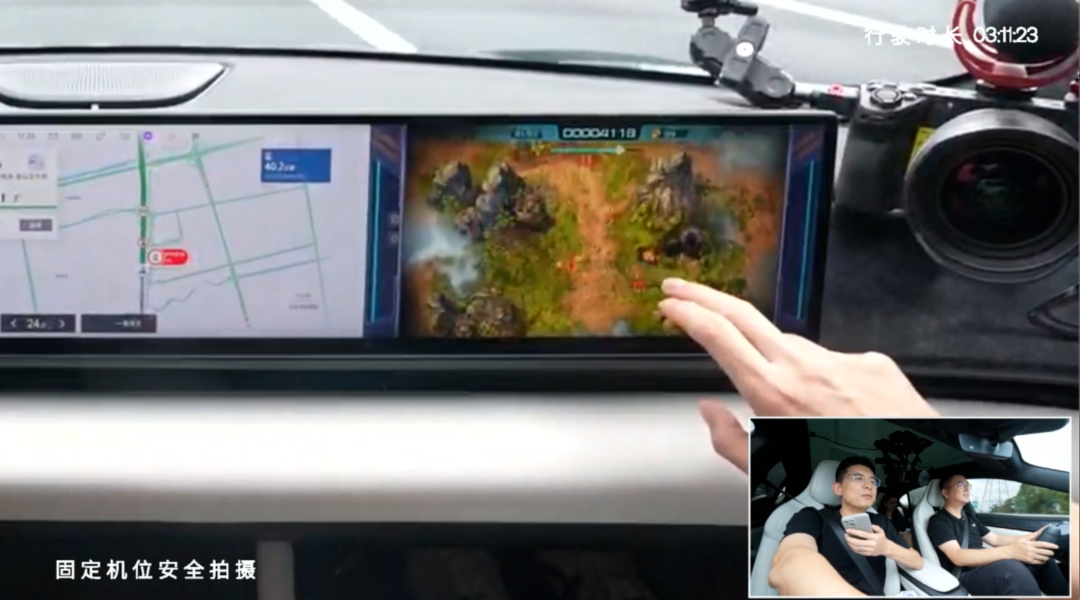
直播过程中，贾秀江展示副驾车载游戏

“我们要做就要做最真实的测试，该开空调开空调、该唱歌唱歌、该打游戏的打游戏，不玩那些虚的，这就是用户最真实的用车场景。”夏一平说。

03｜用户关心的，就是我要亲测的

中午，这台车开到苏州，又开到上海的极越交付中心。夏一平已经开了接近 4 个小时，他有些支撑不住，贾秀江接替他驾驶。

夏一平最近比过去劳累得多。直播过程中，用户建议他改个名字，不叫夏一平了，应该叫“夏一拼”，做 CEO 也太辛苦了。27 日这场十几个小时的全天直播开始前一天，他还拉着团队开交付会议一直到深夜 11 点，前天晚上 2 点才睡，27 日早上 8 点又出现在公司里。

这也不是极越 07 上市后他做的第一场直播了。极越 07 在 9 月 10 日上市，发布会进行了 3 个小时，媒体采访了一个多小时，结束后他就地在北京做了一场车主见面会的直播，持续到零点之后。

两天后，他又跑到徐州做了一场水上浮桥智驾直播。夜晚暗光场景，非标定路面，大弯道，没有车道线，浮桥最窄处仅能支持车辆勉强通过，算是对当下车辆智驾实力最严苛考验之一。好在五次智驾过桥，极越 07 都挑战成功了。

9 月 21 日极越 07 首批交付，他跑到苏州参加交付仪式，也做了一场直播。不只是把钥匙交给车主，他还拉着车主们介绍了一波极越 07 的产品设计细节。

极越 07 交付现场

在当下车企 CEO 们都出来抛头露面做直播的内卷状态下，很难说夏一平的这些直播有多么出类拔萃。刷刷短视频平台你就知道了，过去半年，不管是新车上市，还是续航测试、智驾实测，车企 CEO 们全都拥挤在直播间里。

有老一辈的汽车人第一次面对镜头，长城魏建军、奇瑞尹同跃，也都坐在驾驶座上和用户大谈汽车理念。新势力们更不用说了，小米的雷军、蔚来的李斌、小鹏汽车的何小鹏，时不时还能在直播间中整个活，玩玩梗。

夏一平的直播没有什么突出的，唯一的亮点可能是他足够努力。这次 18 小时的超长直播是一个例子，在那之前他还做过不少堪称“毁车”的实际测试。比如极越 07 上市之前的几场冰冻和撞车测试，一台台崭新的极越 07 拉到测试场地，该撞就撞，推车推着从山坡上滚下来，就是要看看车子在极限条件下的安全性能。

这些测试由头是用户的质疑。极越的车子没有门把手，有用户担忧在冬天或者撞车后，车门会不会打不开？夏一平觉得光靠嘴巴说没有说服力，那就实际测一把。

他们直接把一台极越 07 放到零下 18 度的冷库中冰封 48 小时。48 小时之后，车身全都被一层厚厚的冰封住，四周已经结满了冰锥。这已经是超出日常场景的极限冰冻，但解锁车辆，车门仍然正常开启。

碰撞实验他们做了两次直播。一次在重庆的招商局检测车辆技术研究院，正面、侧面、背面三次撞击后，即便车身都已经变形，车门仍可正常打开。翻滚测试在一个落差 20 米、坡度 45 的山坡上，连续翻滚测试两次，全车结构仍然完好，四个车门都可无障碍开启。

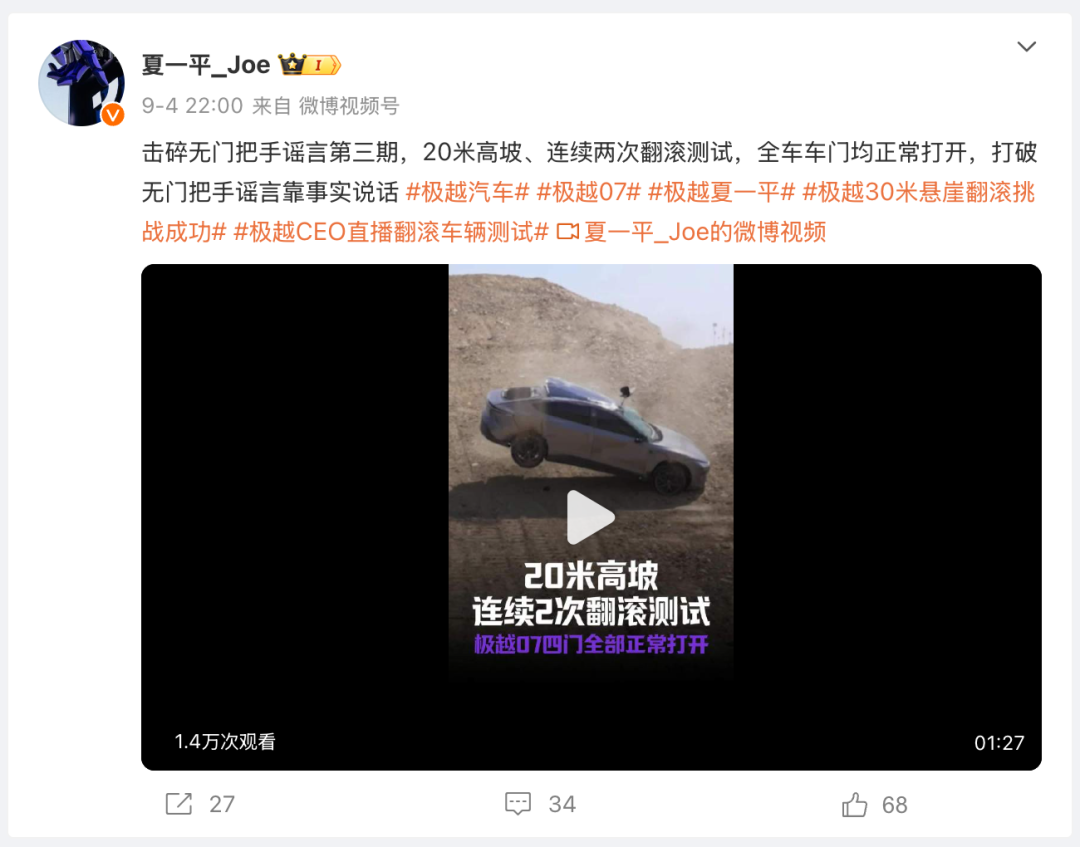
夏一平发布极越 07 翻滚测试视频

“打破无门把手谣言，靠事实说话。”夏一平在社交平台上说。他技术出身，信奉产品的力量，坚信只有产品没问题、底层逻辑对了，事情就一定能成功。

上半年极越 01 销量遇冷，很多人劝他放弃，把重心放到第二款车上，他不信邪，拉着团队狠抓营销，把一台车从月销 100 来台做到月销超 2000 台。最新的 9 月销量，极越交付量已经达到了 2605 台，连续三个月交付量跳跃式增长。

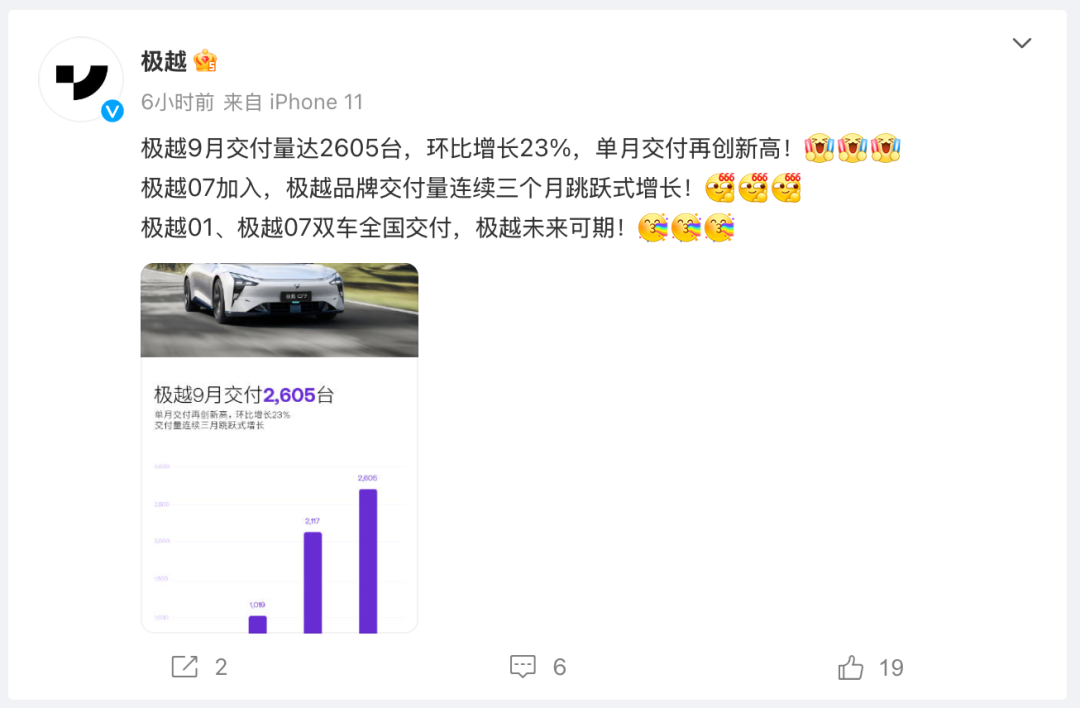
极越 9 月交付量达 2605 台

他也不怕聊那些敏感话题。媒体群访中，他直言他们销量不好，有很多问题，比如只强调了车子的智能化，却忽略了对操控、续航的展示。比如他们的员工发表了有争议的言论，他也拍条视频，端端正正致歉。

“不玩那些虚的。”27 日的这场直播中，夏一平总是在重复这句话。有人在评论区里喊话他们为什么不在冬天测，他说那过几个月就再测一次冬天场景的续航。智驾到底怎么样？他说那就再做一场长距离的智驾直播。总之，他来者不拒，该测就测，靠测试说话。

“用户关心的，就是我要亲测的。”极越 07 的上市发布会上，夏一平在 PPT 上打出一行大字。

04｜凌晨 2 点的狂欢

晚上 11 点，这场直播已经进行了 15 个小时，车子行驶里程超过 680 公里，剩余电量 15%。这已经超出了他们原有的计划。还剩最后几个小时，直播间的观众开始在评论区中猜测最终的续航里程。夏一平乐观估计，最后应该能上 800 公里。

这个数字在接下来几个小时里被证明过于保守。车辆行驶里程很快超过 800 公里，他们开始绕着公司转圈，等待最后的趴窝时刻。

很多用户在这时开始进入直播间。有的人在早上看过直播，深夜再打开手机，发现直播还没结束，顿感惊讶。“这是我看过最真实的续航直播了。”有人在评论区中说。

超长的直播时长引发了用户的种种好奇。你们是怎么上厕所的？怎么能一直开十多个小时？这台车是不是装装了两个电池包？这个电池的化学体系是什么？各种千奇百怪的问题。

夏一平不得不挨个解释，他早上开了 4 个多小时，之后的 10 多个小时一直在车上。“腰没有断，我的身体还是很好的。”不可能装两个电池包的，“你知道一个电池包有多重吗？”

临近结尾，更多汽车行业人士、极越的员工乃至车主开始进入到直播间里。夏一平和一块坐在后排的贾秀江开始回答更多实际的问题。比如他们车机什么时候上线网易云音乐，贾回答说下个版本就会上线。今年线下门店计划开到多少家？夏一平说要到 200 家，应该能完成。全国智驾什么时候上线，第四季度就能推送。

也有人关心起技术细节来。07 的续航为什么这么长？贾秀江从风阻系数聊到电池性能、整车调教，极越 07 的风阻系数做到了 0.198Cd，是同级车型中最优秀的那一档。续航不光和电池容量有关，还和整车的性能优化、三电管理相关。他们车辆使用的是宁德时代的电池，业内最优，底盘采用的是吉利浩瀚架构，耗资不菲，饱经考验。

极越 07 的风阻系数仅为 0.198Cd

直播间中的气氛热烈起来，超过 270 万人看过、点赞量超过 117 万。一些极越线下门店的员工开始在评论区留言，欢迎大家联系试驾。极越车主们开始在评论区中报地名，南京的、深圳的、临沂的还有新疆的，明天就要去苏州提 07 了，夏一平会在现场吗？

这可能是极越成立以来最热闹的一个夜晚。无数观众、员工、车主乃至合作伙伴的眼睛都聚焦在直播间中的汽车屏幕上，凝聚在一起，仿佛在等待火箭升空。

凌晨 1 点多，车辆剩余电量到 0%，车辆行驶路程超过 800 公里，大家开始预计最终的结果。“有点像看奥运比赛的感觉了。”有人评论区中说。最后的半个小时，夏一平的预期目标不断被打破，从 818 公里到 820、830 公里，让人费解车辆的隐藏电量到底还有多少。

夏一平开玩笑说，以前总是担忧车子续航不足，现在觉得续航太长也是一种烦恼。车上的人都已经疲惫不堪，但明显都兴奋起来了。评论区中有人点歌，这会儿应该放一首《难忘今宵》。那时车辆已经到了 830 公里，他们唱起歌来。

830 公里之后，他们绕了一个更大的圈。《难忘今宵》唱完，车子还在跑着，又放了一首《明天会更好》。

夏一平说，这才是最真实的测试。他在直播间中喊话其他车企的 CEO 们，以后直播续航测试，就应该按照这个标准来测试，不搞极端、不搞特调，那些对用户没价值，要做就做最真实场景的测试。

凌晨 2 点，在行驶了 846 公里之后，这台极越 07 终于在一个路口耗尽了电量，停了下来。从电量剩余 0% 算起，这台车足足又跑了 55 公里。

现场的人群爆发出欢呼声，直播间中，评论区齐刷刷地滚动起来。夏一平和极越整车工程负责人王勇开始推车。他说，明早还得开会，今天就睡公司了。

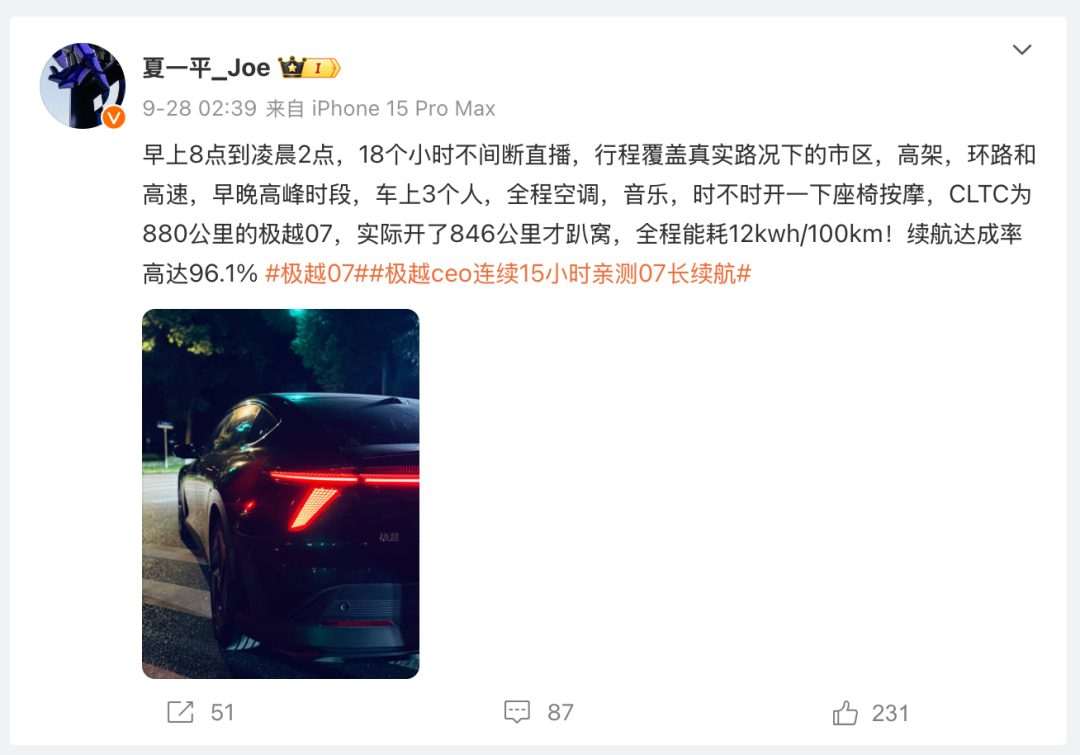
直播结束后，夏一平发布了一条微博