二叉树专题

原创

已于 2025-01-19 11:49:38 修改 · 448 阅读

7 ·

CC 4.0 BY-SA版权

文章标签：

#算法

于 2024-06-18 11:22:22 首次发布

刷LeetCode二叉树题目，简单明了，保证一看就懂的代码。

94. 二叉树的中序遍历

给定一个二叉树的根节点 root ，返回 它的中序遍历 。递归实现【左->根->右】

import java.util.*;
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<Integer>();
        inorder(root, res);
        return res;
    }
    // 递归实现中序遍历
    public void inorder(TreeNode root, List<Integer> res) {
        if (root == null) {
            return;
        }
        inorder(root.left, res);
        res.add(root.val);
        inorder(root.right, res);
    }
}

104. 二叉树的最大深度【递归实现】

给定一个二叉树 root ，返回其最大深度。

二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。

示例 1：

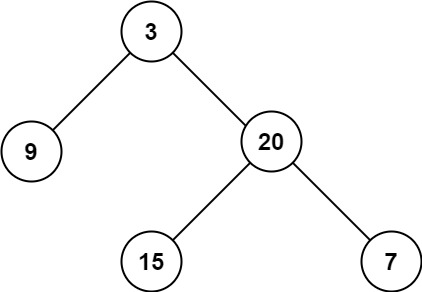
输入：root = [3,9,20,null,null,15,7]
输出：3

示例 2：

输入：root = [1,null,2]
输出：2

提示：

树中节点的数量在 [0, 104] 区间内。
-100 <= Node.val <= 100

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public int maxDepth(TreeNode root) {
       if (root == null) {
            return 0;
        // 递归计算二叉树的高度
        } else {
            int leftHeight = maxDepth(root.left);
            int rightHeight = maxDepth(root.right);
        // 最大高度即为最大深度
            return Math.max(leftHeight, rightHeight) + 1;
        }
    }
}

简化版写法：

public int maxDepth(TreeNode root) {
    if (root == null)
        return 0;
    return Math.max(maxDepth(root.left), maxDepth(root.right)) + 1;
}

111. 二叉树的最小深度

给定一个二叉树，找出其最小深度。

最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

说明：叶子节点是指没有子节点的节点。

public static int minDepth(TreeNode root) {
     if (root == null)
          return 0;
     //如果左子树等于空，我们返回右子树的最小高度+1
      if (root.left == null)
         return minDepth(root.right) + 1;
     //如果右子树等于空，我们返回左子树的最小高度+1
     if (root.right == null)
       return minDepth(root.left) + 1;
    //如果左右子树都不为空，我们返回左右子树深度最小的那个+1
    return Math.min(minDepth(root.left), minDepth(root.right)) + 1;
}

226. 翻转二叉树【递归算法，根->左->右】

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode invertTree(TreeNode root) {
       if(Objects.isNull(root)){
           return null;
       }
       TreeNode tmp=root.right;
       root.right=root.left;
       root.left=tmp;
       // 递归最子树节点
       invertTree(root.left);
       invertTree(root.right);
       return root;
    }
}

101. 对称二叉树【递归的前序遍历】

**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public boolean isSymmetric(TreeNode root) {
        return check(root, root); 
    }
    // 二叉树的前序遍历实现
    public boolean check(TreeNode p, TreeNode q) {
        if (p == null && q == null) {
            return true;
        }
        if (p == null || q == null) {
            return false;
        }
        return p.val == q.val && check(p.left, q.right) && check(p.right, q.left);
    }
}

543. 二叉树的直径【递归的前序遍历】

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    int maxd=0;
    public int diameterOfBinaryTree(TreeNode root) {
        depth(root);
        return maxd;
    }
    public int depth(TreeNode node){
        if(node==null){
            return 0;
        }
        int Left = depth(node.left);
        int Right = depth(node.right);
        // 将每个节点最大直径(左子树深度+右子树深度)当前最大值比较并取大者
        maxd=Math.max(Left+Right,maxd);
        // 所以求直径（即求路径长度的最大值）等效于求路径经过节点数的最大值减,已该节点为起点的加一
        return Math.max(Left,Right)+1;
    }
}

102. 二叉树的层序遍历

import java.util.*;
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List<List<Integer>> levelOrder(TreeNode root) {
        List<List<Integer>> ret = new ArrayList<List<Integer>>();
        if (root == null) {
            return ret;
        }
        Queue<TreeNode> queue = new LinkedList<TreeNode>();
        queue.offer(root);
        while (!queue.isEmpty()) {
            List<Integer> level = new ArrayList<Integer>();
            int currentLevelSize = queue.size();
            for (int i = 1; i <= currentLevelSize; ++i) {
                TreeNode node = queue.poll();
                level.add(node.val);
                if (node.left != null) {
                    queue.offer(node.left);
                }
                if (node.right != null) {
                    queue.offer(node.right);
                }
            }
            ret.add(level);
        }
        return ret;
    }
}

108. 将有序数组转换为二叉搜索树【递归的前序实现】

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode sortedArrayToBST(int[] nums) {
        return helper(nums, 0, nums.length - 1);
    }
    public TreeNode helper(int[] nums, int left, int right) {
        if (left > right) {
            return null;
        }
        // 总是选择中间位置左边的数字作为根节点,二叉搜索树特点:根节点大于左节点,小于右节点,那么类似二叉搜索树的中序遍历
        int mid = left+(right-left)/2;
        TreeNode root = new TreeNode(nums[mid]);
        // 递归实现
        root.left = helper(nums, left, mid - 1);
        root.right = helper(nums, mid + 1, right);
        return root;
    }
}

98. 验证二叉搜索树

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNod