输入一个长度为n的整型数组array，数组中的一个或连续多个整数组成一个子数组，子数组最小长度为1。求所有子数组的和的最大值。
import java.util.*;
public class Solution {
/**
* 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
*
*
* @param array int整型一维数组
* @return int整型
*/
public int FindGreatestSumOfSubArray (int[] array) {
// write code here
if(array.length==1){
return array[0];
}
int max=array[0];
for(int i=1;i<array.length;i++){
// 如果前一位元素>0,直接与本元素相加
if(array[i-1]>0){
array[i]=array[i]+array[i-1];
}
if(array[i]>max){
max=array[i];
}
}
return max;
}
}
输入整数数组arr，找出其中最小的k个数。例如，输入4、5、1、6、2、7、3、8这8个数字，则最小的4个数字是1、2、3、4。
传统排序算法：
// 获取数组的最小的K个数
public int[] getLeastNumbers(int[] arr, int k) {
//先排序，然后选择前k个即可
Arrays.sort(arr);
int[] res = new int[k];
for (int i = 0; i < k; ++i) {
res[i] = arr[i];
}
return res;
}
大根堆解法如下：
// 获取数组的最小的K个数
public int[] getLeastNumbersForPriorityQueue(int[] arr,int k){
if(k==0){
return new int[0];
}
// 构造大顶堆
PriorityQueue<Integer> priorityQueue = new PriorityQueue<>((num1,num2) -> num2- num1);
// 现在堆中放入前K个元素
for(int i=0;i<k;i++){
priorityQueue.offer(arr[i]);
}
for(int i=k;i<arr.length;i++){
if(arr[i]>priorityQueue.peek()){
priorityQueue.poll();
priorityQueue.offer(arr[k]);
}
}
// 最后再把堆中元素转换为数组
int[] result=new int[k];
for(int i=0;i<k;i++){
result[i]=priorityQueue.poll();
}
return result;
}
给定一个按照升序排列的整数数组 nums，和一个目标值 target。找出给定目标值在数组中的开始位置和结束位置。
// 二分查找,然后找到从找到的位置开始
public int[] searchRange(int[] nums,int target){
int find=searchRangeHelp(nums,target);
if(find==-1){
return new int[]{-1,-1};
}
int first=find-1;
int last=find+1;
while(first>=0&&nums[first]==target){
first--;
}
while(last<nums.length&&nums[last]==target){
last++;
}
return new int[]{first+1,last-1};
}
// 二分查找
public int searchRangeHelp(int[] nums, int target){
int low=0;
int high=nums.length-1;
while(low<=high){
int mid=low+(high-low)/2;
int midVal=nums[mid];
if(midVal>target){
high=mid-1;
}else if(midVal<target){
low=mid-1;
}else{
return mid;
}
}
return -1;
}
给定字符串 s 和 t ，判断 s 是否为 t 的子序列。
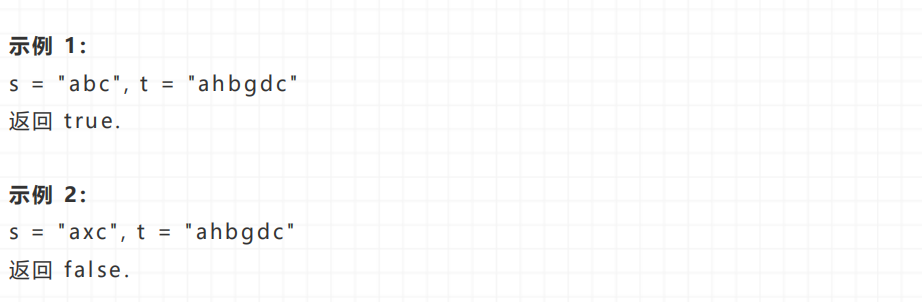
给定一个字符串，找到它的第一个不重复的字符，并返回它的索引。如果不存在，则返回 -1。
public int firstUniqChar(String s) {
for(int i=0;i<s.length();i++){
if(s.indexOf(s.charAt(i))==s.lastIndexOf(s.charAt(i))){
return i;
}
}
return -1;
}
public int firstUniqCharForMap(String s){
Map<Character,Integer> hahMap = new HashMap<>();
for(int i=0;i<s.length();i++){
hahMap.put(s.charAt(i),hahMap.getOrDefault(s.charAt(s.charAt(i)),0));
}
for(int i=0;i<s.length();i++){
if(hahMap.get(s.charAt(i))==1){
return s.charAt(i);
}
}
return -1;
}
给定无序数组arr，返回其中最长的连续序列的长度(要求值连续，位置可以不连续,例如3,4,5,6为连续的自然数）
public int maxLongStr(int[] num){
// 边界条件
if(num.length==0){
return 0;
}
// 最长的有序序列
int longResult=1;
// 记录当前的最长序列
int count=1;
Arrays.sort(num);
for(int i=1;i<num.length;i++){
if(num[i]==num[i-1]){
continue;
}
if(num[i]-num[i-1]==1){
count++;
// 不满足连续序列,count=1
}else{
count=1;
}
longResult=Math.max(longResult,count);
}
return longResult;
}
给定一个字符串，验证它是否是回文串，只考虑字母和数字字符，可以忽略字母的大小写。
// 判断是否是回文字符串
public boolean isPalindrome(String s) {
int left=0,right=s.length()-1;
while(left<right){
// 左指针处理,如果不是字符和数字就过滤掉
while(left<right&!Character.isLetterOrDigit(s.charAt(left))){
left++;
}
while (left<right&!Character.isLetterOrDigit(s.charAt(right))){
right--;
}
// 判断左右指针所在值是否相等
if(Character.toLowerCase(s.charAt(left))!=Character.toLowerCase(s.charAt(right))){
return false;
}
left++;
right--;
}
return true;
}
给定一个非空字符串s，最多删除一个字符。判断是否能成为回文字符串。
// 双指针实现-使用两个指针left和right，从字符串的两边相向而行，如果两个
//指针指向的字符不相同，说明不能构成回文串，我们可以删除一个。可以删除left指向的
//字符也可以删除right指向的字符，
public boolean validPalindrome(String s) {
int left=0;
int right=s.length()-1;
while(left<right){
if(s.charAt(left)!=s.charAt(right)){
return isPalindromic(s,left+1,right)||isPalindromic(s,left,right-1);
}
}
return true;
}
// 判断子串[left,right]是否是回文串逻辑
private boolean isPalindromic(String s, int left, int right) {
while (left < right) {
if (s.charAt(left++) != s.charAt(right--)) {
return false;
}
}
return true;
}
给定一个字符串，请你找出其中不含有重复字符的最长子串的长度。
// 给定一个字符串，请你找出其中不含有重复字符的最长子串的长度。
// 使用队列,每次加入队列前判断是否有相同的值,如果有就出队,如果没有就加入
public int lengthOfLongestSubstring(String s) {
Queue<Character> queue=new LinkedList<>();
int max=0;
for(char c:s.toCharArray()){
if(queue.contains(c)){
queue.poll();
}
queue.offer(c);
max=Math.max(max,queue.size());
}
return max;
}
给定两个数组，编写一个函数来计算它们的交集。
public int[] intersect(int[] nums1, int[] nums2) {
Arrays.sort(nums1);
Arrays.sort(nums2);
int i=0;
int j=0;
List<Integer> result=new ArrayList<>();
while (i<nums1.length&&j<nums2.length){
// 如果数组1的相同位置值小于数组2,左指针向前
if(nums1[i]<nums1[j]){
i++;
}else if(nums1[i]>nums2[j]){
j++;
}else{
result.add(nums1[i]);
// 左右指针同时向前
i++;
j++;
}
}
int[] num=new int[result.size()];
for(int z=0;z<result.size();z++){
num[z]=result.get(z);
}
return num;
}
给你一个有序数组nums ，请你原地删除重复出现的元素，使每个元素只出现一次 ，返回删除后数组的新长度。要求：不要使用额外的数组空间，必须在原地修改输入数组并在使用O(1)额外空间的条件下完成。
public int removeDuplicates(int[] A) {
//边界条件判断
if (A == null || A.length == 0) {
return 0;
}
int count = 0;//重复的数字个数
for (int right = 1; right < A.length; right++) {
if (A[right] == A[right - 1]) {
// 如果有重复的,count要加1
count++;
} else {
// 如果没有重复,数组往后移动
A[right - count] = A[right];
}
}
// 数组的长度减去重复的个数
return A.length - count;
}
前缀和求解方案：
所谓前缀和就是数组中前面n个元素的和，比如：前缀和pre[i]的值是：pre[i]=nums[0]+nums[1]+……+nums[i];前缀和pre[j]的值是：pre[j]=nums[0]+nums[1]+……+nums[i]+nums[i+1]+……+nums[j];如果我们要求子数组[i……j]之间所有元素的和，也就是nums[i]+nums[i+1]+……+nums[j]=pre[j]-pre[i-1]；推导过程：
- 根据前缀和定义，
pre[j] = nums[0] + nums[1] + ... + nums[j]pre[i-1] = nums[0] + nums[1] + ... + nums[i-1]- 两者相减时，公共部分
nums[0] + ... + nums[i-1]被抵消，剩余nums[i] + ... + nums[j]。- 统一公式：
sum[i..j] = pre[j+1] - pre[i]（适用于所有i ≤ j）。示例对比
- 原数组：
nums = [1, 2, 3]（长度3）- 前缀和：
pre = [0, 1, 3, 6]（长度4）
pre[0] = 0（基准）pre[1] = nums[0] = 1pre[2] = nums[0]+nums[1] = 3pre[3] = nums[0]+nums[1]+nums[2] = 6计算
[1,2]区间和（nums[1]+nums[2] = 5）：pre[3] - pre[1] = 6 - 1 = 5pre[3]−pre[1]=6−1=5
给定一个整数数组和一个整数k ，你需要找到该数组中和 为 k 的 连 续 的 子 数 组 的 个数。
也就是说如果pre[j] -pre[i -1]等于k，说明我们找到了一个和为k个连续子数组。
public int subarraySum(int[] nums, int k) {
int[] pre = new int[nums.length + 1];
for (int i = 0; i < nums.length; i++) {
pre[i + 1] = pre[i] + nums[i];
}
int count = 0;
Map<Integer, Integer> map = new HashMap<>();
for (int j = 0; j <= nums.length; j++) {
//计算pre[i-1]+pre[j]=k,我们只需要找出pre[i-1]
int other = pre[j] - k;
if (map.containsKey(other)) {
//如果map中存在pre[i-1],个数进行累加
count += map.get(other);
}
//pre[j]的个数加1在放到map中
map.put(pre[j], map.getOrDefault(pre[j], 0) + 1);
}
return count;
}
给你两个字符串数组word1和word2。如果两个数组表示的字符串相同，返回true；否则，返回false。数组表示的字符串是由数组中的所有元素按顺序连接形成的字符串。
public boolean arrayStringsAreEqual(String[] word1, String[] word2) {
StringBuilder s1 = new StringBuilder();
StringBuilder s2 = new StringBuilder();
//拼接word1中的字符串
for (int i = 0; i < word1.length; i++)
s1.append(word1[i]);
//拼接word2中的字符串
for (int i = 0; i < word2.length; i++)
s2.append(word2[i]);
//比较这两个拼接之后的字符串是否相等
return s1.toString().equals(s2.toString());
}
在一个 n * m 的二维数组中，每一行都按照从左到右递增的顺序排序，每一列都按照从上到下递增的顺序排序。请完成一个函数，输入这样的一个二维数组和一个整数，判断数组中是否含有该整数。
// 暴力破解
public boolean findNumberInTwoDArray(int[][] matrix, int target){
if(matrix==null||matrix.length==0||matrix[0].length==0){
return false;
}
int rows = matrix.length, columns = matrix[0].length;
for(int i=0;i<rows;i++){
for(int j=0;j<columns;j++){
if(matrix[i][j]==target){
return true;
}
}
}
return false;
}
从右上角开始找有个方便的地方就是他左边的都是比他小的，他下边的都是比他大的，
如果target大于当前值我们就往下边找，如果target小于当前值我们就往左边找，来看
下代码。
// 线性查找
public boolean findNumberInTwoDArrayForIndexSearch(int[][] matrix, int target){
if(matrix==null||matrix.length==0||matrix[0].length==0){
return false;
}
int rows=matrix.length,columns=matrix[0].length;
// 从右上角开始遍历查找
int row=0,column=columns-1;
while (row < rows && column >= 0) {
int current=matrix[row][column];
// 如果等于该值
if(current==target){
return true;
// 如果当前值大于目标值,就从左边开始查找
}else if(current>target){
column--;
// 如果当前值小于目标值,就从下边开始查找
}else{
row++;
}
}
return false;
}
给定一个包含了一些0和1的非空二维数组grid 。一个岛屿是由一些相邻的1(代表土地)构成的组合，这里的「相邻」要求两个1必须在水平或者竖直方向上相邻。你可以假设grid的四个边缘都被0（代表水）包围着。找到给定的二维数组中最大的岛屿面积。(如果没有岛屿，则返回面积为0。)
public int maxAreaOfIsland(int[][] grid) {
int maxArea = 0;
int rows=grid.length,columns=grid[0].length;
for(int i=0;i<rows;i++){
for(int j=0;j<columns;j++){
// 如果当前位置为1
if(grid[i][j]==1){
maxArea=Math.max(maxArea,dfsArea(grid,i,j));
}
}
}
return maxArea;
}
private int dfsArea(int[][] grid, int i, int j) {
// 边界判断
if (i >= 0 && i < grid.length && j >= 0 && j < grid[0].length && grid[i][j] == 1) {
//已经访问过了,置为0，然后再从他的上下左右四个方向开始查找
grid[i][j] = 0;
return 1 + dfsArea(grid, i + 1, j) + dfsArea(grid, i - 1, j) + dfsArea(grid, i, j - 1) + dfsArea(grid, i, j + 1);
}
return 0;
}
给你一个按照非递减顺序排列的整数数组
nums，和一个目标值target。请你找出给定目标值在数组中的开始位置和结束位置。如果数组中不存在目标值
target，返回[-1, -1]。
class Solution {
public int singleNonDuplicate(int[] nums) {
int ret=0;
for(int i=0;i<nums.length;i++){
ret=ret^nums[i];
}
return ret;
}
}
给你两个按 非递减顺序 排列的整数数组
nums1和nums2，另有两个整数m和n，分别表示nums1和nums2中的元素数目。请你 合并
nums2到nums1中，使合并后的数组同样按 非递减顺序 排列。
class Solution {
public void merge(int[] nums1, int m, int[] nums2, int n) {
int i = m - 1, j = n - 1;
// 新数组的长度,从后面开始遍历
// 时间复杂度O(m+n)
// 空间复杂度O(1)
int index = m + n - 1;
while (i >= 0 || j >= 0) {
// 对应长度相等时候
if (i >= 0 && j >= 0) {
nums1[index--] = nums1[i] >= nums2[j] ? nums1[i--] : nums2[j--];
// 对应数组1元素剩余,排在前面即可
} else if (i >= 0) {
nums1[index--] = nums1[i--];
// 对应数组2元素剩余,排在前面即可
} else {
nums1[index--] = nums2[j--];
}
}
}
}
给你一个整数数组
nums，其中元素已经按 升序 排列，请你将其转换为一棵 平衡 二叉搜索树。
class Solution {
public TreeNode sortedArrayToBST(int[] nums) {
return helper(nums, 0, nums.length - 1);
}
public TreeNode helper(int[] nums, int left, int right) {
if (left > right) {
return null;
}
// 总是选择中间位置左边的数字作为根节点,二叉搜索树特点:根节点大于左节点,小于右节点,那么类似二叉搜索树的中序遍历
int mid = left+(right-left)/2;
TreeNode root = new TreeNode(nums[mid]);
// 递归实现
root.left = helper(nums, left, mid - 1);
root.right = helper(nums, mid + 1, right);
return root;
}
}
给你一个字符串
s，由若干单词组成，单词前后用一些空格字符隔开。返回字符串中 最后一个 单词的长度。单词 是指仅由字母组成、不包含任何空格字符的最大子字符串。
class Solution {
public int lengthOfLastWord(String s) {
// 最后一个单词长度
int index = s.length() - 1;
while (s.charAt(index) == ' ') {
index--;
}
int wordLength = 0;
while (index >= 0 && s.charAt(index) != ' ') {
wordLength++;
index--;
}
return wordLength;
}
}
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
