程序设计week11 作业

最新推荐文章于 2022-08-30 16:14:02 发布
原创 最新推荐文章于 2022-08-30 16:14:02 发布 · 430 阅读 · 0 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文精选了多项算法竞赛题目，包括房价预测与购房策略、矩阵旋转对比、凯撒密码解密、连续数字最大配对、ATM取款最优策略及唱片收集问题。深入解析了动态规划、数学模型、字符串处理、数据结构等核心算法，提供了详细的代码实现。

A-必做题11-1

蒜头君从现在开始工作，年薪 NN 万。他希望在蒜厂附近买一套 6060 平米的房子，现在价格是 200200 万。假设房子价格以每年百分之 KK 增长，并且蒜头君未来年薪不变，且不吃不喝，不用交税，每年所得 NN 万全都积攒起来，问第几年能够买下这套房子？（第一年年薪 NN 万，房价 200200 万）

输入格式
一行，包含两个正整数 N(10 \le N \le 50)N(10≤N≤50)，K(1 \le K \le 20)K(1≤K≤20)，中间用单个空格隔开。

输出格式
如果在第 2020 年或者之前就能买下这套房子，则输出一个整数 MM，表示最早需要在第 MM 年能买下；否则输出"Impossible"。

输出时每行末尾的多余空格，不影响答案正确性

样例
输入
50 10
输出
8

解题思路
房价为 200 * pow( 1+ K/100 , i-1 )
工资为 i * N

比较2个的大小即可

代码实现

#include<iostream>
#include<cmath>
using namespace std;

float N;
float K;
int main()
{
	cin>>N>>K;
	float a;
	float b;
	int flag=0;
	float i;
	for(i=1;i<=20;i++)
	{
		a = i * N;
		b = 200 * pow((1+K/100),i-1);
		
		if(a>=b) {
			cout<<i<<endl;
			flag++;
			return 0;
		}
	}
	if(flag==0)
	{
		cout<<"Impossible"<<endl;
		return 0;
	}
	
	return 0;
}

B - 必做题 11-2

在这里插入图片描述

样例输入

4
0 0 0 0
0 0 0 0
0 1 0 0
0 0 0 0
0 0 0 0
0 1 0 0
0 0 0 0
0 0 0 0

样例输出
1

解题思路
顺时针90度 ---- [ i , j ] ----> [ j , n+1-i]
顺时针180度 -------[ i , j ] -----> [ n+1-i , n+1-j ]
顺时针270度 ------- [ i , j] -------> [ n+1-j ,i]

把当前矩阵和目标矩阵进行比较就可以了

代码

#include<iostream>
using namespace std;

bool a[25][25];
bool b[25][25];
int n;

bool _1()
{
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=n;j++)
		{
			if(a[i][j]!=b[i][j]) return 0;
		}
	}
	return 1;
}
bool _2()
{
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=n;j++)
		{
			if(a[i][j]!=b[j][n+1-i]) return 0;
		}
	}
	return 1;
}
bool _3()
{
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=n;j++)
		{
			if(a[i][j]!=b[n+1-i][n+1-j]) return 0;
		}
	}
	return 1;
}
bool _4()
{
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=n;j++)
		{
			if(a[i][j]!=b[n+1-j][i]) return 0;
		}
	}
	return 1;
}

int main()
{
	cin>>n;
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=n;j++)
		{
			cin>>a[i][j];
		}
	}
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=n;j++)
		{
			cin>>b[i][j];
		}
	}
	if(_1()) {cout<<0<<endl;return 0;}
	if(_2()){cout<<1<<endl;return 0;}
	if(_3()){cout<<2<<endl;return 0;}
	if(_4()){cout<<3<<endl;return 0;}
	cout<<-1<<endl;
	return 0;
}

C - 必做题11-3

在这里插入图片描述

样例
NS BFW, JAJSYX TK NRUTWYFSHJ FWJ YMJ WJXZQY TK YWNANFQ HFZXJX

IN WAR, EVENTS OF IMPORTANCE ARE THE RESULT OF TRIVIAL CAUSES

解题思路

把一行字符串全部读取到string里面，
用getline(cin,str) , 
可以连同空格一起读入，如果只是用cin的话，遇到空格和回车就会停止

用 str[i] = (str[i]-'A'+26-5)%26+'A' 
来将该字符退回到前5个

代码

#include<iostream>
#include<string>
using namespace std;
string str;


bool jud(int i)
{
	char c[] = {'A','B','C','D','E','F','G','H','I','J','K','L','M','N','O','P','Q','R','S','T','U','V','W','X','Y','Z'};
	for(int j=0;j<26;j++)
	{
		if(c[j]==str[i]) return 0;
	}
	return 1;
}

int main()
{
	getline(cin,str);
	
	for(int i=0;i<str.size();i++)
	{
	
		if(jud(i)) continue;
		else
		{
			str[i] = (str[i]-'A'+26-5)%26+'A' ;
		
		}
	}
	cout<<str<<endl;
	return 0;
}

D - 必做题11-4

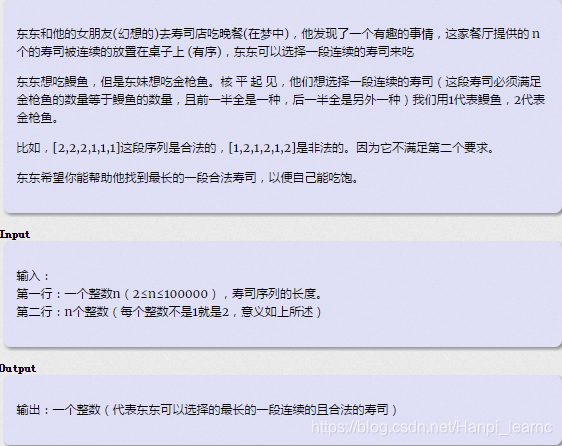
在这里插入图片描述

Examples
Input
7
2 2 2 1 1 2 2
Output
4
Input
6
1 2 1 2 1 2
Output
2
Input
9
2 2 1 1 1 2 2 2 2
Output
6

解题思路

1.想办法把一段相同的个数个记录下来，例如11112222，记为4 4
2.然后把能够拿走的个数给记录下来，例如 11122221111，很显然为 3 4 
3.比较2中所有记录的大小，取出最大的

代码实现

#include<iostream>
#include<algorithm>
#include<vector>
using namespace std;
const int N = 1e5+10;
int a[N];
vector<int> b;
int main()
{
	int n;
	cin>>n;
	for(int i=0;i<n;i++)
	{
		cin>>a[i];
	}
	int sum1=0;
	int flag=a[0];
	a[n] = -1;
	for(int i=0;i<=n;i++)  //第一步
	{
		if(flag==a[i])
		{
			sum1++;
			flag=a[i];
		}
		else
		{
			b.push_back(sum1);
			sum1=1;
			flag = a[i];
		}
	}

    int ai=0;
	for(int i=0;i<b.size()-1;i++) //第二步 
	{
		if(b[i]>b[i+1])
		{
			a[ai++] = b[i+1];
		}
		else
		{
			a[ai++] = b[i];
		}
	}
	sort(a,a+ai);         //第三步
	cout<<a[ai-1]*2;
	return 0;
}

E - 选做题11-1 东东与 ATM ( 多重背包+二进制拆分 == 0 1 背包 ）

在这里插入图片描述

Sample Input
735 3  4 125  6 5  3 350
633 4  500 30  6 100  1 5  0 1
735 0
0 3  10 100  10 50  10 10
Sample Output
735
630
0
0

在这里插入图片描述

解题思路

1.多重背包 （一开始我写多重背包的代码，但是超时了）

代码

#include<iostream>
using namespace std;
const int N=100005;
struct W{
	int _nk_ , _dk_ ;  //_dk_ -- 面额  _nk_ 数量 
};

W w[15];
int f[15][N];

int main()
{
	int cash,n,nk,dk;  //cash总量 n面额数量 nk是dk的数量 dk是面额 
	while(cin>>cash>>n){
	for(int i=1;i<=n;i++)
	{
		cin>>w[i]._nk_>>w[i]._dk_;
//		cout<<w[i]._dk_<<" "<<w[i]._nk_<<endl;
	}
	//initial
	for(int i=0;i<=N;i++)
		f[0][i] = 0;
	
	//多重背包
	for(int i=1;i<=n;i++)
	{
		for(int j=0;j<=cash;j++)
		{
			f[i][j] = f[i-1][j];
	//		cout<<"1.fij="<<f[i][j]<<endl;
			for(int k=1;k<=w[i]._nk_;k++)
			{
				if(j - k * w[i]._dk_ >= 0){
					f[i][j] = max(f[i][j] ,f[i-1][j-k*w[i]._dk_]+k*w[i]._dk_);	
			//		cout<<"2.f["<<i<<","<<j<<"]="<<f[i][j]<<endl;
				}
			}
		}
	}
	int m=f[n][cash];
	cout<<m<<endl;
	}
	return 0;
 } 

2.二进制拆分后 ，还要转换成 01背包进行求解，不然可能会超空间
3.二进制拆分的思路：
例子： 111111 拆成 1 + 10 + 100 + 1000 + 100000.......
如果不能刚好拆完，则最后剩下的那个数也算为拆分的一部分

为什么要二进制拆分？
通过二进制拆分，可以转换成01背包
例如 111 = 1 + 10 + 100  ，本来是要在 111里面进行一个for循环遍历的（多重背包）
但是如果把他拆分了，就可以转换成 01 ，选或者不选，如果1 10 100全部都选了，加起来就是111 ，相当于在多重背包里面把这种物体选完了。
多重背包的那部分复杂度降为了log
但是还是不行，因为如果 f【】【】是二维的，是会超空间的
所以要用一维数组实现

代码

#include<iostream>
#include<vector>
#include<algorithm>
#include<cstring>
using namespace std;
const int N=100005;
int cash,n,nk,dk;  //cash总量 n面额数量 nk是dk的数量 dk是面额 
struct W{
	int _nk_ , _dk_ ;  //_dk_ -- 面额  _nk_ 数量 
};

W w[15];
int ww[N];
int index;
int f[N];

void acc()   //二进制拆分 
{
	index=0;
	for(int i=1 ; i<= n ;i++)  //第i种面额 
	{
		int c = w[i]._nk_;
		for(int j=1;j<= c ;j<<=1)
		{
			index++;
			ww[index] = j*w[i]._dk_; 
			c -= j;
		 } 
		 if(c > 0)
		 {
		 	index++;
		 	ww[index] = c*w[i]._dk_;
		 }
	}
}

void ini() //初始化
{
	memset(ww,0,sizeof(ww));
	for(int i=0;i<15;i++)
	{
		w[i]._dk_=0;
		w[i]._nk_=0;
	}
	
	memset(f,0,sizeof(f));
}

int main()
{
	
	while(cin>>cash>>n){
	ini();
	for(int i=1;i<=n;i++)
	{
		cin>>w[i]._nk_>>w[i]._dk_;
	}

	acc();

	//01 背包 
	for(int i=1; i<=index; i++)
	{
		for(int j=cash;j>=ww[i];j--)
		{
		f[j] = max(f[j] ,f[j-ww[i]]+ww[i]);
		}
	}
	cout<<f[cash]<<endl;
	}
	return 0;
 }

F - 选做题11-2 东东开车了

在这里插入图片描述

Sample Input
5 3 1 3 4
10 4 9 8 4 2
20 4 10 5 7 4
90 8 10 23 1 2 3 4 5 7
45 8 4 10 44 43 12 9 8 2
Sample Output
1 4 sum:5
8 2 sum:10
10 5 4 sum:19
10 23 1 2 3 4 5 7 sum:55
4 10 12 9 8 2 sum:45

解题思路

01背包求解 （需要用到的是二维的数组）
倒推过程
详情看代码注释

代码

#include<iostream>
#include<cstdio>
#include<vector>
#include<algorithm>
#include<cstring>
using namespace std;

int N,M;
int m[25];
int f[25][10005];
int a[25];

void ini()   //初始化
{
	memset(a,0,sizeof(a));
	memset(f,0,sizeof(f));
	memset(m,0,sizeof(m));
}

int main()
{
	while(cin>>N>>M)
	{
		ini();
		for(int i=1;i<=M;i++)
		cin>>m[i];

		//01背包
		for(int i=1;i<=M;i++)
		{
			for(int j=0;j<=N;j++)
			{
				f[i][j] = f[i-1][j];
				if(j>=m[i])
				{					
					f[i][j] = max( f[i][j] , f[i-1][j-m[i]] + m[i] );

				}
			}
		 }
	
		
		//倒推
		int b = N;
		for(int i=M;i>=1;i--)
		{
			if(f[i][b]>f[i-1][b])   //如果(f[i][b]>f[i-1][b]) 
			{						//则代表该状态选择了a【i】
				a[i] = 1;			
				b -=m[i];
			}
		 }
		 
		 for(int i=1;i<=M;i++)
		 {
		 	if(a[i]==1)         //如果为1 ，则该唱片被选择
		 	{
		 		cout<<m[i]<<" ";
			 }
		  }
		  cout<<"sum:"<<f[M][N]<<endl;
		  
	}
	
	return 0;
}
程序设计思维与实践 Week11 作业
ErHaH_H的博客
05-01 275
1、必做题11-1 蒜头君从现在开始工作，年薪 N 万。他希望在蒜厂附近买一套 60 平米的房子，现在价格是 200 万。假设房子价格以每年百分之 K 增长，并且蒜头君未来年薪不变，且不吃不喝，不用交税，每年所得 N 万全都积攒起来，问第几年能够买下这套房子？（第一年年薪 N 万，房价 200 万） 输入格式 一行，包含两个正整数 N(10≤N≤50)，K(1≤K≤20)，中间用单个空格隔开。 输...
山东大学计算机科学与技术学院程序设计思维与实践作业 week11-动态规划（1）
m0_57734028的博客
07-10 2136
山东大学计算机科学与技术学院程序设计思维与实践作业 山大程序设计思维与实践作业 sdu程序设计思维与实践 山东大学程序设计思维实践作业H11 山大程序设计思维实践作业H11 山东大学程序设计思维与实践 week11-动态规划（1） 动态规划相关资料：GitHub题目描述 楼上有 n 级台阶，其中有 m 级台阶是不安全的。yhf 一开始站在第 0 级台阶上，希望最终走到第 n 级台阶 yhf 跨一步满足以下约束： • 只能向前走 • 不能落脚在不安全的台阶上 • 最多迈 k 级台阶 • 落脚点不能超过第 n
Week11 - 程序设计思维与实践 - 动态规划（二）
Keep eating codes!
05-03 316
必做题 必做题与DP没啥关系，难度为 CSP T1、T2 级别 A - 必做题11-1 题意 蒜头君从现在开始工作，年薪 NNN 万。他希望在蒜厂附近买一套 606060 平米的房子，现在价格是 200200200 万。假设房子价格以每年百分之 KKK 增长，并且蒜头君未来年薪不变，且不吃不喝，不用交税，每年所得 NNN 万全都积攒起来，问第几年能够买下这套房子？（第一年年薪 NNN 万，房价 2...
程序设计思维与实践 Week11 A~D
banzixiang的博客
05-02 229
A: 思路： 即不断循环，循环中每次对蒜头君手里的钱加60万，对房价乘以（1+k/100）,直到大于的时候输出年数。同时如果循环中超过20年，则输出Impossible。 代码： #include <iostream> using namespace std; int main(){ double N,K; cin>>N>>K; K=K/100; ...
程序设计思维与实践 Week11
Xu Pengbo
05-07 1069
Problem A-买房子 Description 蒜头君从现在开始工作，年薪 NN 万。他希望在蒜厂附近买一套 6060 平米的房子，现在价格是 200200 万。假设房子价格以每年百分之 KK 增长，并且蒜头君未来年薪不变，且不吃不喝，不用交税，每年所得 NN 万全都积攒起来，问第几年能够买下这套房子？（第一年年薪 NN 万，房价 200 万） Input 一行，包含两个正整数 N(10≤N≤...
SDU 程序设计思维与实践Week11 东东与 ATM【多重背包】
weixin_43975891的博客
04-30 304
东东与 ATM 一家银行计划安装一台用于提取现金的机器。 机器能够按要求的现金量发送适当的账单。 机器使用正好N种不同的面额钞票，例如Dk，k=1,2,…,ND_k，k = 1,2,…,NDk​，k=1,2,…,N，并且对于每种面额D_k，机器都有n_k张钞票。 例如， N=3，n1=10，D1=100，n2=4，D2=50，n3=5，D3=10N = 3， n_1 = 10，D_1 = 100，...
基于JavaScript及微信小程序开发的week18平时作业设计源码
09-29
本项目“基于JavaScript及微信小程序开发的week18平时作业设计源码”正是这样一个结合了微信小程序和JavaScript技术的实际开发案例。 首先，JavaScript作为脚本语言在本项目中扮演着至关重要的角色。它不仅负责小...
程序设计思维与实践 Week9 作业 B 东东学打牌
01-06
A, 2, 3, 4, 5, 6, 7, 8, 9, 10, J, Q, K 分别指代 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13。 每个玩家抽得 5 张扑克牌，组成一手牌！（每种扑克牌的张数是无限的，你不用担心，东东家里有无数副扑克牌） ...
程序设计思维与实践 Week8 作业
GoodPeople233的博客
04-17 304
A - 区间选点 II 题目： 给定一个数轴上的 n 个区间，要求在数轴上选取最少的点使得第 i 个区间 [ai, bi] 里至少有 ci 个点 使用差分约束系统的解法解决这道题 使用差分约束系统的解法解决这道题 使用差分约束系统的解法解决这道题 使用差分约束系统的解法解决这道题 使用差分约束系统的解法解决这道题 Input 输入第一行一个整数 n 表示区间的个数，接下来的 n 行，每一行两个...
山大程序设计思维与实践作业week1-算法复杂度与程序调试
m0_57734028的博客
07-01 2763
山东大学计算机科学与技术学院程序设计思维与实践作业 山大程序设计思维与实践作业 sdu程序设计思维与实践 山东大学程序设计思维实践作业H1 山大程序设计思维实践作业H1 山东大学程序设计思维与实践 程序设计思维与实践 week1-算法复杂度与程序调试 相关资料：GitHub问题描述 给出一个长度为 3 的字符串，所有字母均为大写英文字母，请判断该字符串是否由同一个字母构成。输入格式 输入一行表示字符串。输出格式 若该字符串是否由同一个字母构成，输出 Won，否则输出 Lost。样例输入 1 TTT 样例输出
SDU程序设计思维与实践 Week11 【必做题】
weixin_43975891的博客
04-30 318
A 蒜头君从现在开始工作，年薪 N万。他希望在蒜厂附近买一套 60 平米的房子，现在价格是 200 万。假设房子价格以每年百分之 K 增长，并且蒜头君未来年薪不变，且不吃不喝，不用交税，每年所得 N万全都积攒起来，问第几年能够买下这套房子？（第一年年薪 N 万，房价 200 万） 输入 一行，包含两个正整数 N(10≤N≤50)N(10≤N≤50)，K(1≤K≤20)K(1≤K≤20)N(10 \...
程序设计思维与实践 Week11 作业 D 必做题11-4
cax1165
05-02 306
题目描述： 东东和他的女朋友(幻想的)去寿司店吃晚餐(在梦中)，他发现了一个有趣的事情，这家餐厅提供的 n 个的寿司被连续的放置在桌子上 (有序)，东东可以选择一段连续的寿司来吃 东东想吃鳗鱼，但是东妹想吃金枪鱼。核 平 起 见，他们想选择一段连续的寿司（这段寿司必须满足金枪鱼的数量等于鳗鱼的数量，且前一半全是一种，后一半全是另外一种）我们用1代表鳗鱼，2代表金枪鱼。 比如，[2,2,2,1...
程序设计思维与实践 Week11 作业 E 选做题11-1 东东与 ATM
cax1165
05-02 415
题目描述： 一家银行计划安装一台用于提取现金的机器。 机器能够按要求的现金量发送适当的账单。 机器使用正好N种不同的面额钞票，例如D_k，k = 1,2,…,N，并且对于每种面额D_k，机器都有n_k张钞票。 例如， N = 3， n_1 = 10，D_1 = 100， n_2 = 4，D_2 = 50， n_3 = 5，D_3 = 10 表示机器有10张面额为100的钞票、4张面额为50的钞票...
关于C语言中浮点数的输入输出格式问题
热门推荐
Guoqing_Lin的博客
08-30 1万+
对C语言中 float, double, 和 long double 类型的浮点数的输入输出格式进行小结，同时对 %f, %e, %g 的区别进行了讨论，结尾对部分系统可接受采用 %lf 输出的问题作了简短解释。
程序设计思维 week11 作业
qq_26239785的博客
05-03 357
A 题意 蒜头君从现在开始工作，年薪 NN 万。他希望在蒜厂附近买一套 6060 平米的房子，现在价格是 200200 万。假设房子价格以每年百分之 KK 增长，并且蒜头君未来年薪不变，且不吃不喝，不用交税，每年所得 NN 万全都积攒起来，问第几年能够买下这套房子？（第一年年薪 NN 万，房价 200200 万） 输入格式 一行，包含两个正整数 N(10 \le N \le 50)N(10≤N≤5...
第11周 动态规划二
zzh000307的博客
05-05 352
11.1.买房问题 题目描述： 蒜头君从现在开始工作，年薪 N 万。他希望在蒜厂附近买一套 60平米的房子， 现在价格是 200 万。假设房子价格以每年百分之 K 增长，并且蒜头君未来年薪不变， 且不吃不喝，不用交税，每年所得 N 万全都积攒起来，问第几年能够买下这套房子？ （第一年年薪 N 万，房价 200 万） 输入描述： 一行，包含两个正整数 N(10≤N≤50)， K(1≤K≤20)，中间...
程序设计思维与实践 Week11 作业 必做题 A-蒜头君买房子
qq_43666020的博客
05-07 817
题目链接：A-蒜头君买房子 题目描述： 蒜头君从现在开始工作，年薪N万。他希望在蒜厂附近买一套60平米的房子，现在价格是 200万。假设房子价格以每年百分之K增长，并且蒜头君未来年薪不变，且不吃不喝，不用交税，每年所得N万全都积攒起来，问第几年能够买下这套房子？（第一年年薪N万，房价200万） Input： 一行，包含两个正整数N(10≤N≤50)，K(1≤K≤20)，中间用单个空格隔开。 Out...
买房子问题（break，continue，return的区别）
C++ 转战 Java
11-28 908
问题描述： 蒜头君从现在开始工作，年薪NN万。他希望在蒜厂附近买一套6060平米的房子，现在价格是200200万。假设房子价格以每年百分之KK增长，并且蒜头君未来年薪不变，且不吃不喝，不用交税，每年所得NN万全都积攒起来，问第几年能够买下这套房子？（第一年年薪NN万，房价200200万） 输入格式 一行，包含两个正整数N(10 \le N \le 50)N(10...
程序设计思维与实践 Week11 作业 A 必做题11-1
cax1165
05-02 449
题目描述： 蒜头君从现在开始工作，年薪NN万。他希望在蒜厂附近买一套6060平米的房子，现在价格是200200万。假设房子价格以每年百分之KK增长，并且蒜头君未来年薪不变，且不吃不喝，不用交税，每年所得NN万全都积攒起来，问第几年能够买下这套房子？（第一年年薪NN万，房价200200万） input： 一行，包含两个正整数N(10 \le N \le 50)N(...
山东大学程序设计作业week4
最新发布
03-18
### 山东大学程序设计 Week4 作业题目解决方案 关于山东大学程序设计课程的 Week4 作业，虽然当前提供的引用并未直接提及 Week4 的具体内容[^1]，但从类似的编程竞赛和算法训练来看，Week4 很可能涉及图论基础、...
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值