数据中心 c++ || 最小生成树

样例
input
4
5
1
1 2 3
1 3 4
1 4 5
2 3 8
3 4 2
output
4

解题思路
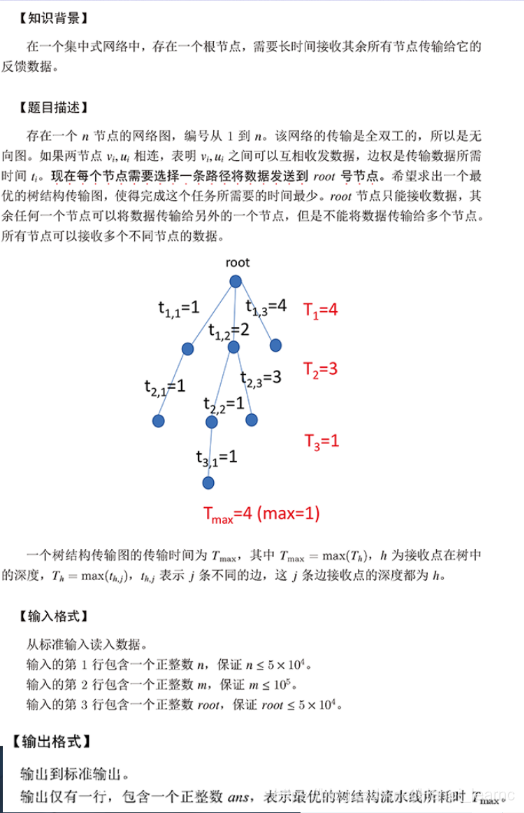
1.题目很长，大意是求出所有生成树里面，边和最小的最大边。

2.求最小的最大，我们可以使用二分答案。

3.也可以先求最小生成树，然后再求最大边。

代码实现

#include<iostream>
#include<algorithm>
using namespace std;
const int Max = 100005;
const int Max_n = 50005;
struct edge{
	int u_,v_,w_;
	bool operator<( const edge &e )
	{
		if(w_!=e.w_)  return w_<e.w_;
		else return 1;
	}
} e[Max];
int ei;
void addE(int u,int v ,int w)
{
	edge E;
	E.u_=u,E.v_=v,E.w_=w;
	e[ei++] = E;
}
//并查集部分，判断是否形成环路
int par[Max_n];
int M[Max_n];
int find(int x)
{
	if(x==par[x])  return x;
	else  return par[x] = find(par[x]);
}
int ini(int n)
{
	for(int i=0;i<=n;i++)
	{par[i]=i;M[i]=1;}
}
bool unite( int x,int y)
{
	x = find(x),y=find(y);
	if(x==y) return 0;
	if(M[x]>M[y])  par[y] = par[x],M[x]+=M[y];
	else par[x] = par[y] , M[y]+=M[x];
	return 1;
}

int n,m,root;
int main()
{
	cin>>n>>m>>root;
	int u,v,w;
	ini(n);
	for(int i=0;i<m;i++)
	{
		cin>>u>>v>>w;
		addE(u,v,w);
	}
	sort(e,e+ei);
	int cn=0,a=0;
	for(int i=0;i<ei;i++)
	{
		if(unite(e[i].u_,e[i].v_)){
		a=max(a,e[i].w_);
		if( ++cn>n )  break;}
	}
	cout<<a<<endl;
	return 0;
}

小结
这题实现起来似乎不是太难，但关键是题目太长了，而且还有点读不懂题目，当知道是求最小生成树的最大边时，很快就能写出来。