卡尔曼滤波器中的Q,R

点击蓝字关注我们

关注、星标公众号，精彩内容每日送达
来源：网络素材

卓老师，我想问一个关于卡尔曼滤波的问题，希望您能解答一下。之前我用的互补滤波效果也还好，但在用卡尔曼滤波的时候出现了一些问题：就是如何整定卡尔曼滤波的Q、R这两个参数，这两个参数分别是角度数据置信度与角速度数据置信度。我看别人用的这两个参数都非常小，比如别人Q都是零点零零几，而我用的时候发现Q零点几跟随效果很差，我把Q调到1跟随效果才差不多。但是Q和R不都是协方差吗，它们可以取到1及以上的值吗？即Q和R有没有取值范围，以及这两个参数整定方法是什么？还是我理解有问题，希望卓大或者车友可以解答一下。

回复：在智能车竞赛中，Kalman滤波算法常常被用来计算直立车模倾角和转动角速度。算法利用陀螺仪给出的转速度量和加速度传感器给出的倾角观测量完成计算。除了Kalman滤波器算法之外，还可以使用互补滤波器进行帮助计算。

如果不考虑系统状态的时变性和系统噪声的时变性，上述两种方法本质上是相同的。

下图显示了对于被测物体位置使用Kalman滤波算法来估计物体实际位置的示意图。

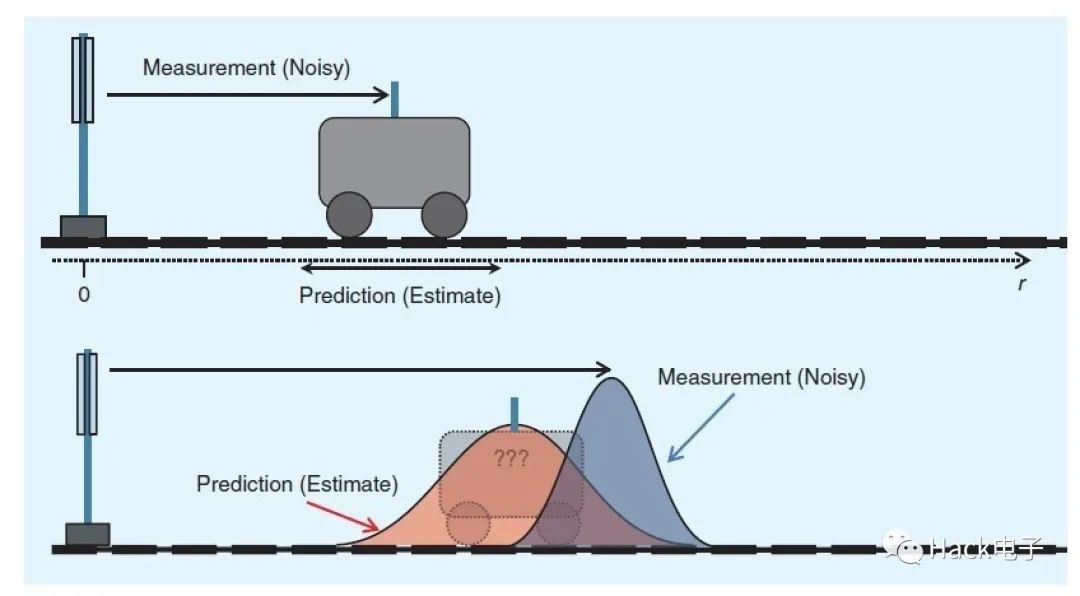
通常情况下所使用的Kalman滤波器是离散时间系统形式的。我们真正想得到的物理量表示成系统状态中的某些分量。对于系统状态的估计（滤波结果）所使用的信息来源于两个方面，一个是对系统状态演变模型的了解，包括系统转移矩阵和输入控制矩阵，输入孔质量等，另一方面来自于对系统状态的观测量。

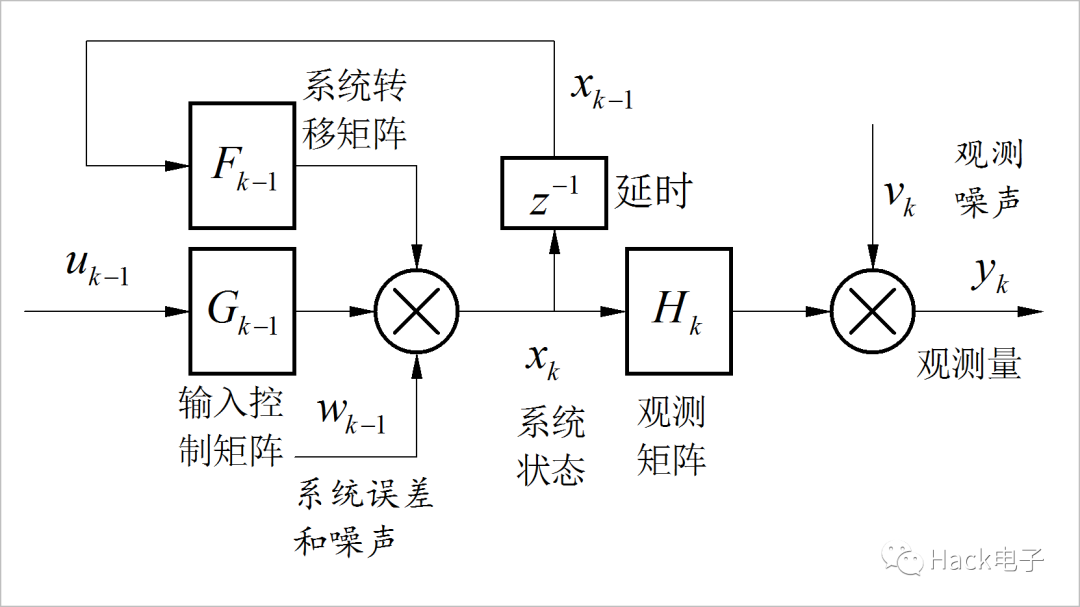
但这两方面的信息都会有某种不确定性。通常使用系统噪声向量（W）和观测噪声向量（V）来表示。两个噪声大小分别使用它们各自的协方差矩阵来表示。系统噪声协方差矩阵使用Q，观测噪声的协方差矩阵使用R。

下面是系统方程和观测方程表达式。虽然在表达式中包括了系统噪声w和转测噪声v，但在计算系统状态转移和系统观测量的时候并不考虑这两个噪声的影响。

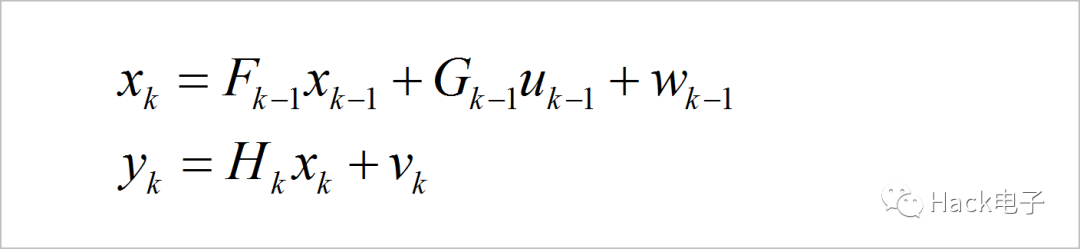
两个噪声的影响只是在卡尔曼滤波器离散迭代算法过程中使用到了两个噪声的协方差矩阵Q和R。分别用于计算系统状态估计误差的协方差矩阵P和卡尔曼滤波器增益K的大小。

下面是传统线性卡尔曼滤波器的五个基本迭代公式。

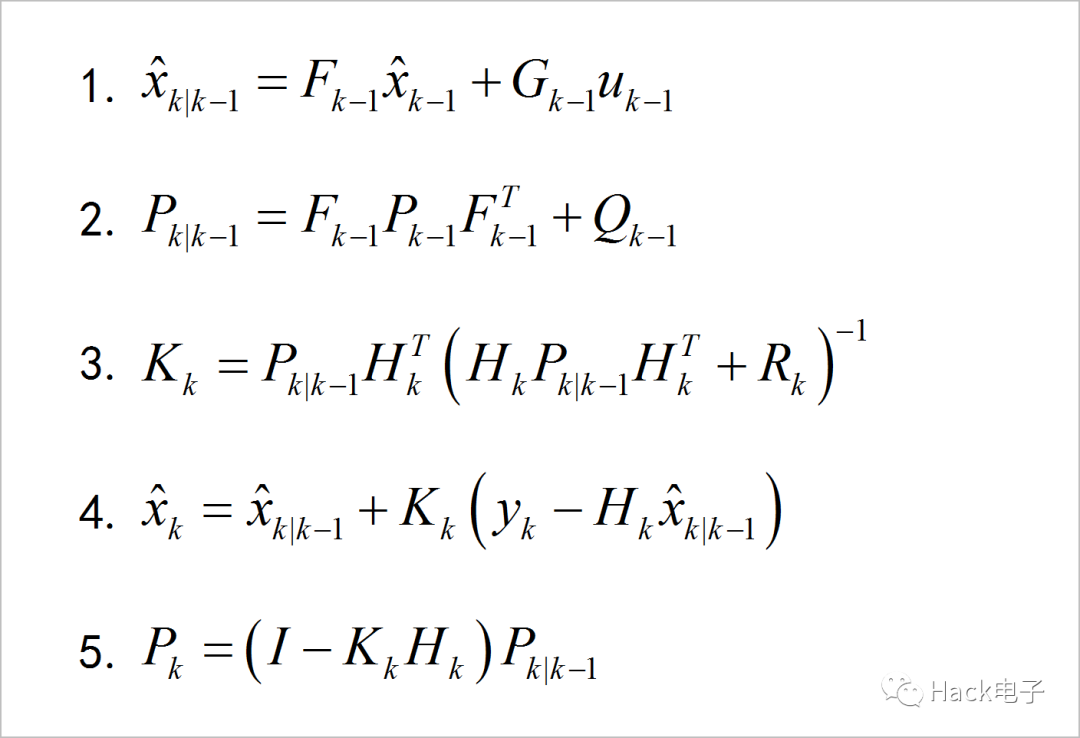
从上面公式来看，真正所要滤波得到的结果来自于公式（4）中的系统状态估计值x的某些分量，公式（4）的结果是由公式（1）所得到的状态预测值和来自观测量y计算得到的。其中卡尔曼滤波器增益K是在状态预测值和观测误差值之间做了一个折中。

如果K很小，比如等于0，则滤波结果更加接近由系统状态估计值给出的递归结果；如果K很大，比如等于1，则滤波结果更加接近于观测值所反算出来的状态变量。

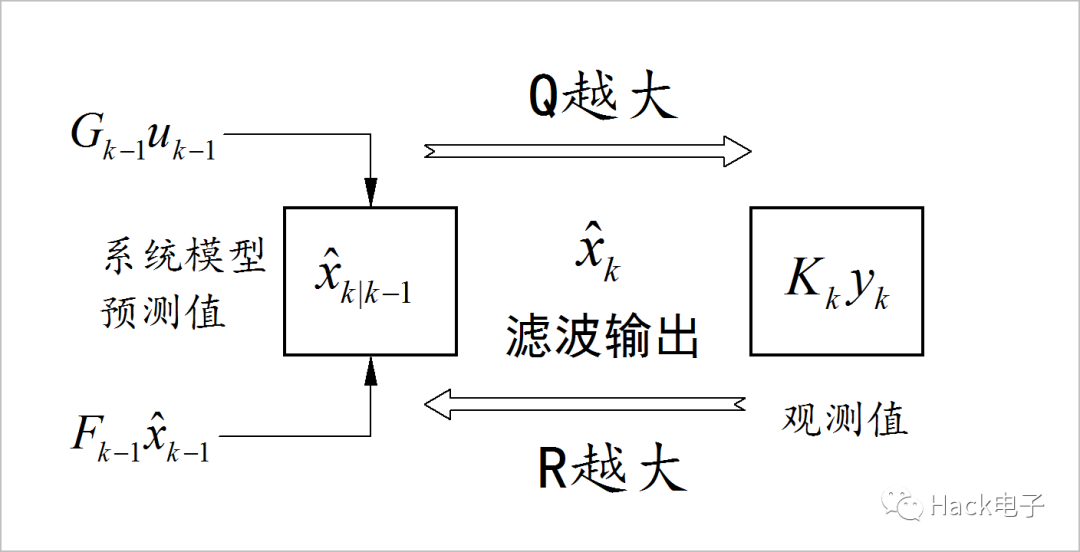
K值是由公式（3）计算获得，其中的P值是通过公式（2）（5）进行计算，反映了Q的大小，因此K值的大小可以由如下形式示意：

因此，K值至于Q,R的比值有关系，而与Q,R的绝对值没有关系。所以，在不同算法中，R, Q的取值根据反应的不同量纲，可以有很大的变化，但它们的比值会决定了滤波值应该更多来自于系统模型演化的信息，还是来自于观察信号信息。

在智能车竞赛中，使用Kalman滤波器将惯性传感器所得到的车体陀螺仪所反映的角速度和和加速度传感器所获得的倾斜角信息进行融合，获得直立车模倾角和转动角速度。

此时，往往将系统状态x设定为车模需要观察的角度。系统输入量u为测量所得到的角速度；系统观察值设定为有加速度传感器给出的倾角。

系统模型噪声w应该反映出陀螺仪测定角速度的随机误差和随着时间漂移的系统误差两部分。系统观测噪声v应该反映了加速度计输出量中在计算角度的近似误差和由于车模运动所产生的干扰噪声。

如果Q大R小，造成K增加，则滤波结果中就会存在较大的由于车模运动所产生的噪声，俗称跟踪不好；如果Q小R大，造成K减小，则滤波结果会出现两种问题，第一就是从处置值收敛到正确值的过程较慢，需要等一个比较长的稳定时间。另一方面就是会受到陀螺仪本身零点漂移，产生比较大的输出零点误差。

最终这两个参数的大小可以根据所选择的器件的实际性能（噪声，漂移等）通过实验观察的方式获得一个比较好的相对值。

想要了解FPGA吗？这里有实例分享，ZYNQ设计，关注我们的公众号，探索