【宝物筛选】

最新推荐文章于 2025-02-25 20:19:05 发布

原创最新推荐文章于 2025-02-25 20:19:05 发布 · 207 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#c++

文章介绍了一种方法，将多重背包问题通过二进制组合优化为01背包问题，以降低复杂度从O(W*n*m)到O(W*n*log2m)。程序示例展示了如何处理物品种类、载重、价值和重量，使用动态规划求解最大价值。

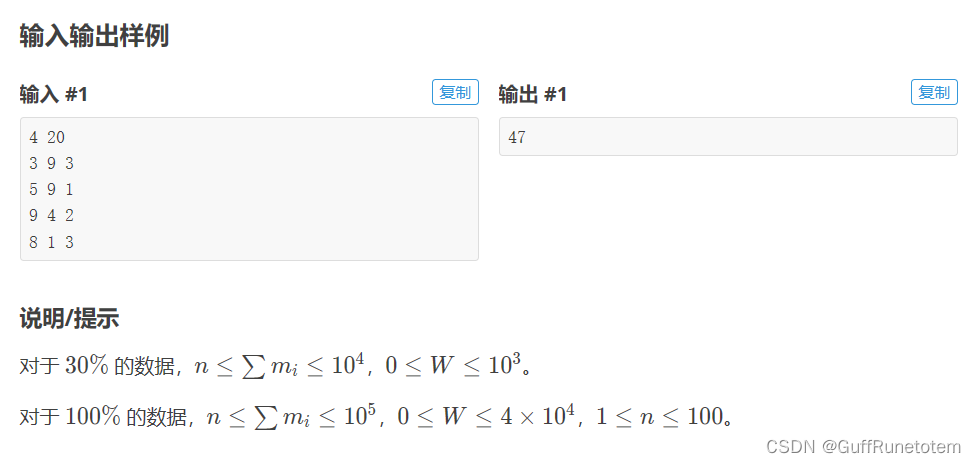
思路：将多重背包问题转化为01背包问题，但是由于复杂度（W*n*m)太大，需要通过二进制提前对同一种类的物品进行组合，以此将复杂度降到（W*n*log2m)。

#include<iostream>
using namespace std;
const int N=1000010;
int n,W,f[N],w[N],v[N];
/* 种类 载重 价值 重量 数量*/
int a,b,c,temp;
int main(){
	cin>>n>>W;
	for(int i=1;i<=n;i++){
		cin>>a>>b>>c;
		for(int j=1;j<=c;j<<=1){
			temp++;
			v[temp]=j*a;
			w[temp]=j*b;
			c-=j;
		}
		if(c){
			temp++;
			v[temp]=c*a;
			w[temp]=c*b;
		}
	}
	for(int i=1;i<=temp;i++)
		for(int j=W;j>=w[i];j--)
			f[j]=max(f[j],f[j-w[i]]+v[i]);
	cout<<f[W];
	return 0;
}