文章包含一系列编程问题的解决方案，涉及动态规划、二分查找、最长上升子序列等算法，以及路径计数、加一操作、网格判断等逻辑判断问题。每个问题都有详细的思路解析和代码实现。
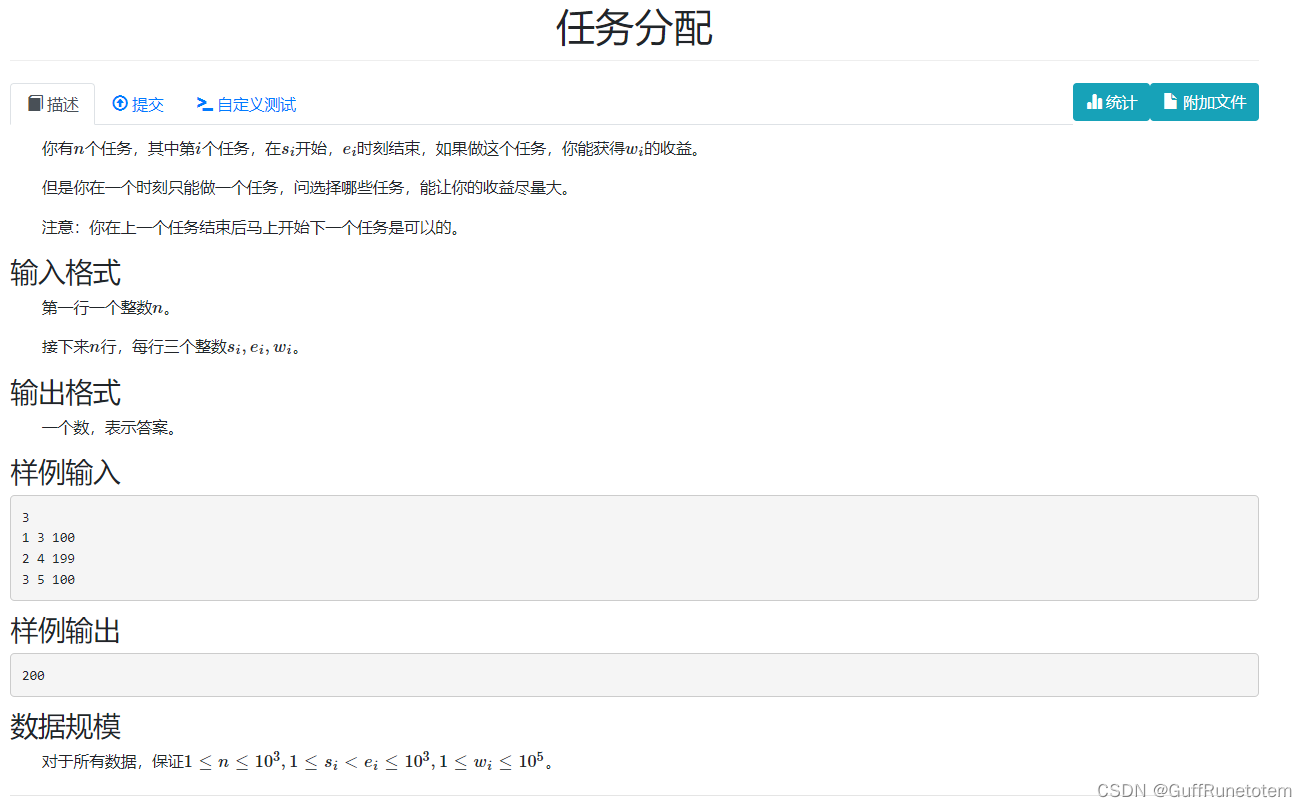
1 任务分配
#include<iostream>
using namespace std;
int f[1005],s[1005],e[1005],w[100005];
int n,maxt;
int main()
{
cin>>n;
for(int i=1;i<=n;i++)
{
cin>>s[i]>>e[i]>>w[i];
maxt=max(e[i],maxt);
}
f[0]=0;
for(int i=1;i<=maxt;i++)
{
f[i]=max(f[i],f[i-1]);
for(int j=1;j<=n;j++)
{
if(s[j]==i)
{
f[e[j]]=max(f[i]+w[j],f[e[j]]);
}
}
}
cout<<f[maxt];
}
思路：动态规划问题。f[i]作为从0到 i 时间段的最大工作收益。当前时刻 i 的收益至少为 i-1 时刻的收益，因此用max判断。以 j 遍历所有任务的开始时间，如果开始时间 s 与当前时刻相同，那么分为两种情况，一是选择该任务，f[ e[ j ] ] （即结束任务的时刻）的收益等于 f[ i ] + w[ j ] ；二是不选该任务，则等于其本身。由此得出动态转移方程。
2 饿饿 饭饭
#include<bits/stdc++.h>
using namespace std;
int n,a[100001];
//a为每个人的饭量（按次序）
int c[100001];
//c为l轮之后队列中的人
long long k;
long long calc(int x){
//x表示为多少轮
long long res=0;
//计数器 = 第x轮后总共打出的饭数量
for(int i=1;i<=n;i++){
if(a[i]<=x)
//如果该人的饭量小于打饭的轮次
res+=a[i];
else
//如果大于。。。
res+=x;
}
return res;
}
int main(){
scanf("%d%lld",&n,&k);
long long s=0;
for(int i=1;i<=n;i++)
scanf("%d",&a[i]),s+=a[i];
//输入+记录需要的饭总量
if(s<k){
//判断-1情况
//s是需要的饭总量
//k小于s，则阿姨打完之前就没人了
printf("-1\n");
return 0;
}
int l=0,r=1e9;
while(l+1<r){
int m=(l+r)/2;
if(calc(m)<=k)
l=m;
else
r=m;
}
int lastk=k-calc(l);
//最后一轮打饭数=总打饭次数-l轮后打出的次数
int tot=0;
for(int i=1;i<=n;i++){
if(a[i]>l)
//如果该人饭量大于l
c[++tot]=i;
//加入最后第l+1轮的队列
}
for(int i=lastk+1;i<=tot;i++){
printf("%d ",c[i]);
}
/*注意是最后一轮，先打到的人排队尾去了，
先输出最后一轮没打到的人*/
for(int i=1;i<=lastk;i++){
if(a[c[i]]!=l+1)
printf("%d ",c[i]);
}
/*再输出打到且还没吃饱的人，
注意判断a[c[i]]的饭量是否大于l+1
（注意+1）
*/
}
思路：见代码注释，主要在于用二分法寻找打完 k 次饭之前总共会打多少轮（m），注意饭量小的同学在 m 轮后是否还在。最后一轮的打饭时注意先打到的同学会向后排队（或出队）。同时，注意 -1 的判断是总需求饭量与 k 值进行比较。
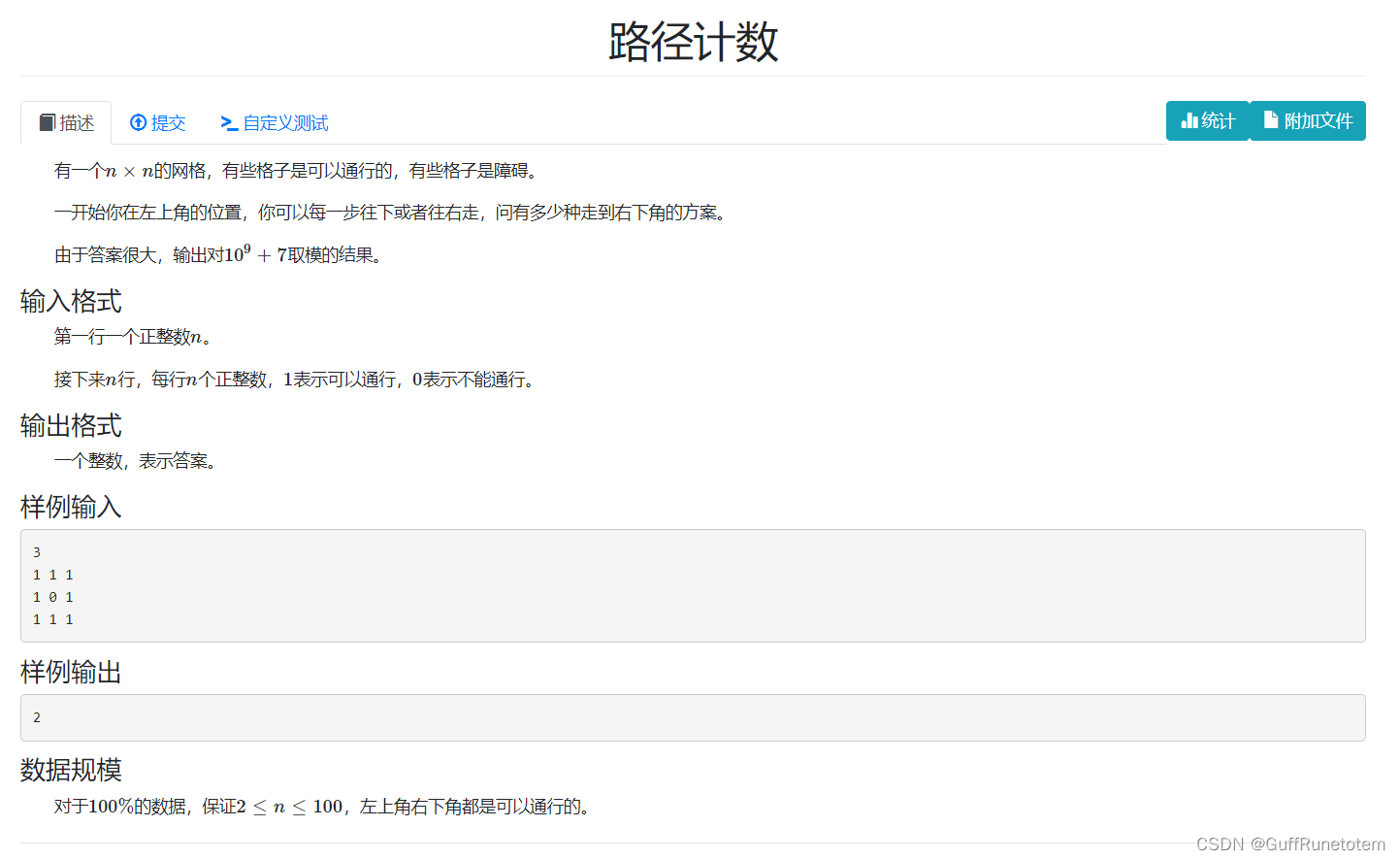
3 路径计数
#include<bits/stdc++.h>
using namespace std;
int n;
long long ans;
const long long mod=1e9+7;
int maze[200][200];
long long f[200][200];
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++)
scanf("%d",&maze[i][j]);
}
f[1][1]=1;
//初始位置一定能走到
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
if(maze[i][j]==1){
f[i][j]+=f[i-1][j];
f[i][j]%=mod;
f[i][j]+=f[i][j-1];
f[i][j]%=mod;
}
else{
f[i][j]=0;
}
// cout<<f[i][j]<<" ";
}
// cout<<'\n';
}
cout<<f[n][n]%mod<<endl;
return 0;
}
思路：这是一道动态规划题目。f [ i ] [ j ] 代表到达该点的路径总数，由于只有向右和向下两种方向，因此转移方程首先判断该点是否可达（为1），其次加上 f [ i-1] [ j ]和 f [ i ][ j-1 ] 。为保证不越界，每次加完后都需要取模。最后输出 f [ n ] [ n ] 。
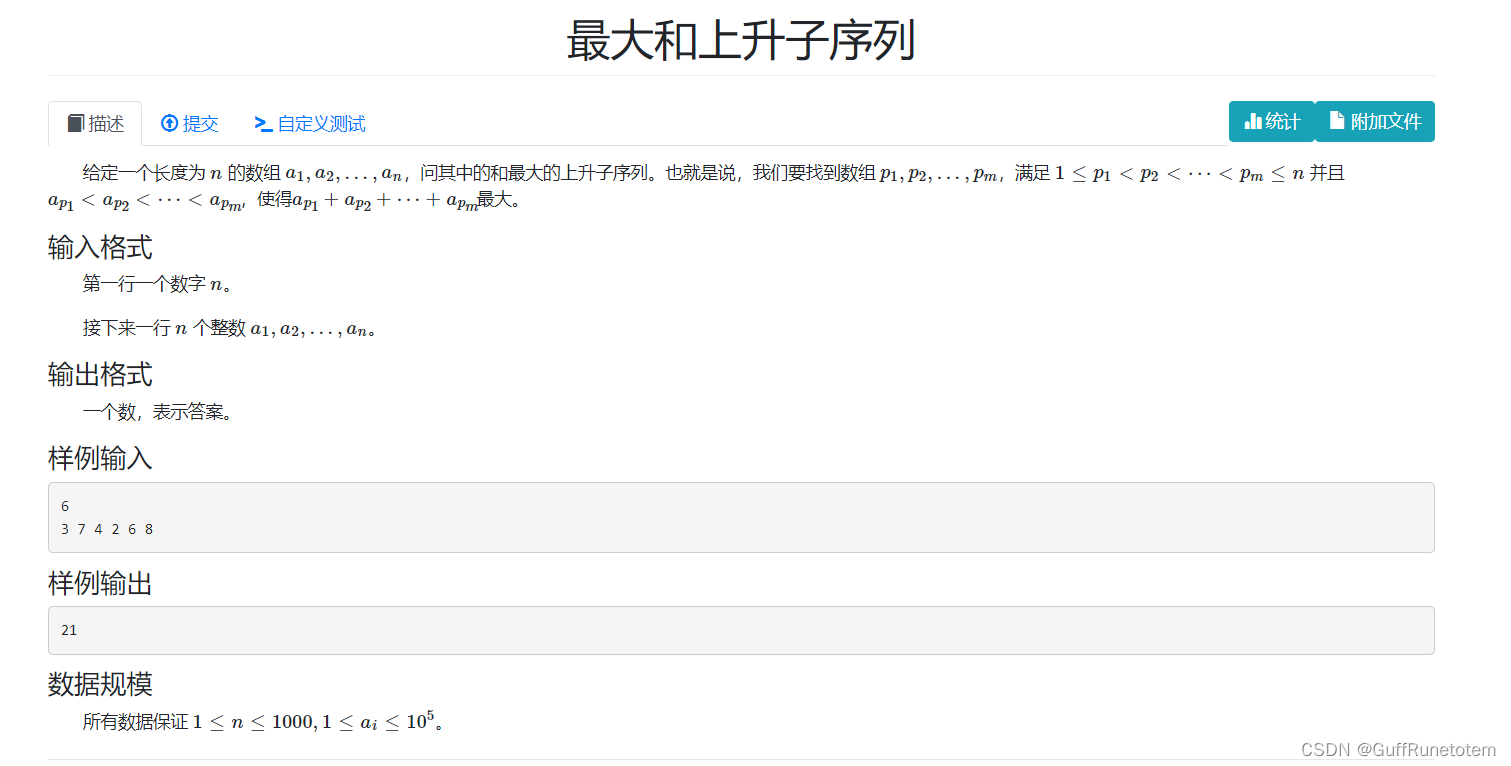
4 最大上升和数列
#include<bits/stdc++.h>
using namespace std;
int f[1005],g[1005];
int n,maxg;
int main(){
cin>>n;
for(int i=1;i<=n;i++){
cin>>f[i];
g[i]=f[i];
}
for(int i=1;i<=n;i++){
//遍历n个数
for(int j=i-1;j>=1;j--){
//所有之前的不比第i个数大的
if(f[i]>=f[j]){
g[i]=max(g[i],g[j]+f[i]);
}
}
}
for(int i=1;i<=n;i++){
maxg=max(g[i],maxg);
// cout<<g[i]<<" ";
}
cout<<maxg;
}
思路：这是一道动态规划问题。考虑两个问题，一个是单调不降数列，一个是求和，因此用两个数组 f 和 g 。由于范围允许，直接用循环。判断第 i 个数字不小于前面某 j 数字后，用转移方程得出到第 i 个数字的最大单调不降数列和。
5 加一
写在前面，这个动态规划的转移方程简直是反人类的，不通过查阅仅凭自己寻找需要对动态规划数据特别敏感。以下先是一个打表找规律的程序，然后是该题的程序。
#include<bits/stdc++.h>
using namespace std;
const int N=1e9+7;
int main(){
vector<char> vec;
vec.push_back('0');
vector<int> tmp;
for (int n=0;n<=100;n++) {
tmp.clear();
for (int i=0;i<vec.size();i++) {
if (vec[i]=='9'){
tmp.push_back(i);
}
vec[i]=char('0'+(vec[i]-'0'+1)%10);
}
for (int i=tmp.size()-1;i>=0;i--) {
vec.insert(vec.begin()+tmp[i],'1');
}
cout<<n<<" "<<vec.size()<<'\n';
}
}
#include<bits/stdc++.h>
using namespace std;
const int mod=1e9+7;
int dp[11][200005];
//dp[n][k] n代表从0-9的数字 k代表进行的操作次数
//dp数组本身存储的是n数字在进行k次操作后的位数
int main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
//读写更快
for(int i=0;i<=9;i++){
//9个数字
for(int j=0;j<=10;j++){
//进行10次以内操作
if(i+j<10) dp[i][j]=1;
//个位
else dp[i][j]=2;
}
}
for(int i=0;i<=9;i++){
for(int k=10;k<=200000;k++){
//进行10次以上操作
dp[i][k]=dp[i][k-9]+dp[i][k-10];
dp[i][k]%=mod;
}
}
int t;
cin>>t;
while(t--){
int n,m;
cin>>n>>m;
int x=n;
long long ans=0;
while(x){
ans+=dp[x%10][m];
//每一位进行m次操作都会增加位数
//ans记录总长度
ans%=mod;
x/=10;
}
cout<<ans<<'\n';
}
}
思路：首先题目问的是进行操作后的长度，不是数字（不会只有我搞错吧）。然后可以预见（每一位数字+操作次数）小于10的情况长度都为1，继续列出后寻找规律：dp [ i ][ k ] = dp [ i ][ k-9 ] + dp[ i ][ k-10 ] 。得到这个规律即可对原数字的每一位进行操作后的长度进行累加运算，注意每次累加后取模，答案不变。
6 跳跳
#include<bits/stdc++.h>
using namespace std;
typedef pair<int,int> pii;
int gcd(int a,int b){
return b? gcd(b,a%b):a;
}
//判断最大公约数
inline void write(int n){
if(n<0){
putchar('-');
n=-n;
}
if(n>=10){
write(n/10);
}
putchar(n%10+'0');
}
//快写
inline int read(){
register int x=0,t=1;
register char ch=getchar();
while('0'>ch||ch>'9'){
if(ch=='-') t=-1;
ch=getchar();
}
while('0'<=ch&&ch<='9'){
x=(x<<3)+(x<<1)+(ch^48);
ch=getchar();
}
return x*t;
}
//快读
int main(){
int n,ans=0,tmp;
int dx,dy;
n=read();
vector<pii>v;
map<pii,int>mp;
int a,b;
for(int i=1;i<=n;i++){
a=read();
b=read();
v.push_back({a,b});
}
for(int i=0;i<n;i++){
for(int j=0;j<n;j++){
if(i==j) continue;
//自己到自己无需跳
dx=v[i].first-v[j].first;
dy=v[i].second-v[j].second;
//两点之间的横、纵轴差
if(dx==0||dy==0){
dx=(dx==0? 0:dx/abs(dx));
dy=(dy==0? 0:dy/abs(dy));
}
//如果其中一个距离为零
//（不会出现相同的点）
//结果最终可以归结为正负1
else{
tmp=abs(gcd(dx,dy));
dx/=tmp;
dy/=tmp;
}
//取最大公约数
//然后约分
if(mp[{dx,dy}]==0){
//这里如果使用数组来判断会超时
//同时需要考虑正负问题
ans++;
mp[{dx,dy}]=1;
}
}
}
write(ans);
return 0;
}
思路：其实是判断有无点在同一条直线上的问题（需要考虑方向）。而由于是整数，所以可以用最大公约数求出“单位”向量（因为可以连续使用同一魔法）。最后通过去重得到答案。
7 最长公共子序列
#include<bits/stdc++.h>
#define up(i,l,r) for(int i=l;i<=r;i++)
#define dn(j,r,l) for(int j=r;j>=l;j--)
using namespace std;
const int N=1e5+5;
int a[N],b[N],dp[N],f[N];
int main(){
int n,x,y,len=1;
scanf("%d",&n);
up(i,1,n){
scanf("%d",&x);
b[x]=i;
//第一组数列只是为了取编号
}
up(i,1,n){
scanf("%d",&x);
a[i]=b[x];
//第二组数列根据第一组数列的编号生成
//与具体数字
}
dp[1]=a[1];
up(i,2,n){
if(a[i]>dp[len]) dp[++len]=a[i];
// 使用二分法找到小于a[i]的某个位置的地址然后存入
// 非常精妙的操作（以下为实例）：
/*
6
1 2 3 4 5 6
1 3 6 2 4 5
*/
// 经过前几次循环后序列为 1 3 6 此时找到 2
// 通过 else 中的二分法更新了序列 1 2 6
// 下一步找到 3
// 继续更新序列 1 2 3
// 这时如果再找到 4 len就会自加，更新答案！
// 否则就会因为 6 导致出错
else{
// cout<<"replace"<<*lower_bound(dp+1,dp+1+len,a[i])<<"\n";
// 可以用来测试
*lower_bound(dp+1,dp+1+len,a[i])=a[i];
}
}
// up(i,1,n){
// f[i]=1;
// }
// int max_f=f[1];
// up(i,2,n){
// dn(j,i-1,1){
// if(a[i]>a[j]){
// f[i]=max(f[i],f[j]+1);
// }
// }
// max_f=max(f[i],max_f);
// }
// printf("%d\n",max_f);
// 明显注释掉的这部分是常规判断最长子序列的方法
// 但会导致程序超时
printf("%d\n",len);
}
思路：将第二组数列按第一组数列出现的顺序从 1 - n 编号，然后求最长子序列即为答案。其余见代码注释。
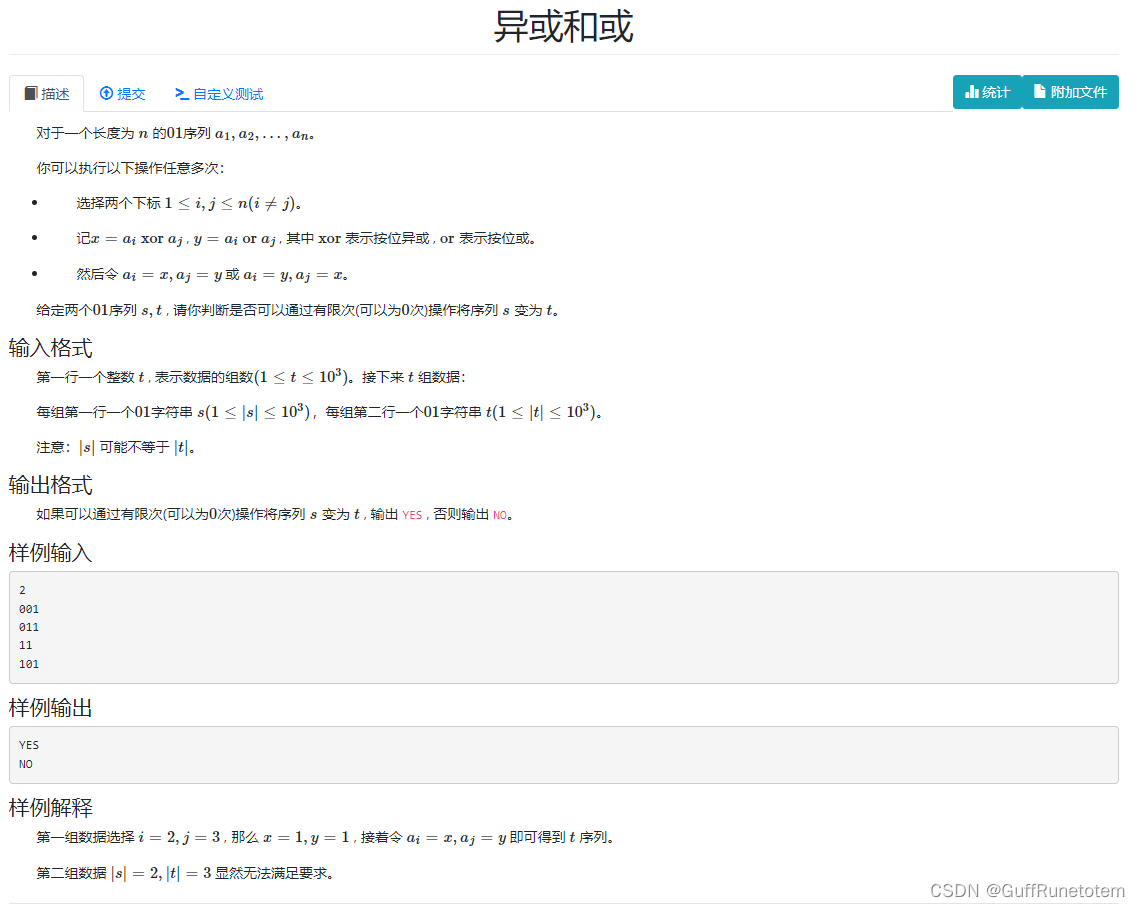
8 异或和或
#include<bits/stdc++.h>
//#include<cstring>
using namespace std;
const int N=1e4+10;
int n;
char s[N],t[N];
bool flags,flagt;
int main(){
ios::sync_with_stdio;
cin.tie(0);
cout.tie(0);
cin>>n;
while(n--){
cin>>s;
cin>>t;
flags=false;
flagt=false;
//!!!注意每次要重新赋值！！！
if(strlen(s)!=strlen(t)){
cout<<"NO"<<endl;
}
//如果长度不一致
else{
for(int i=0;i<strlen(s);i++){
if(flags==true&&flagt==true){
break;
}
if(!flags&&s[i]=='1'){
flags=true;
}
//只要有一项为1，所有数都可变为1
//10 可变为 11
if(!flagt&&t[i]=='1'){
flagt=true;
}
}
if(flags!=flagt){
//一列有1，一列没有
cout<<"NO"<<endl;
}
else{
//两种情况，都有1或全为0
cout<<"YES"<<endl;
}
}
}
return 0;
}
思路：这是一道结论题。
0 0 所有变化都是 0 0
1 1 变化为 1 0 或 0 1
0 1 和 1 0 变化为 1 1
思考发现只要数列中有 1 就可以把所有数都变为 1 。同时可发现 s 到 t 是 t 到 s 的逆变化，因此可以将全部为 1 的数列当作中转数列。问题转化为判断两个数列中是否都有 1 或者全部为 0 。同时如果长度不一致，特判输出NO即可。
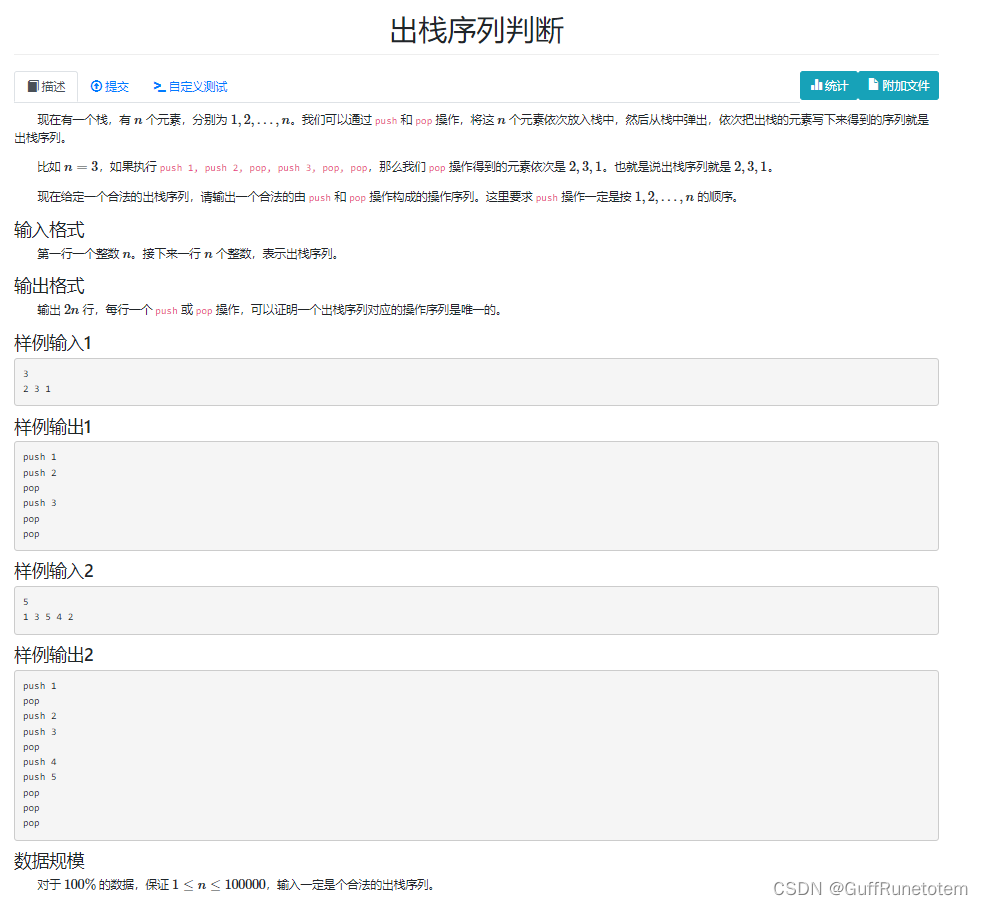
9 出栈序列判断
#include<iostream>
//#include<bits/stdc++.h>
//#include<stack>
//注意该头文件下stack需更换变量名
using namespace std;
const int N=100005;
inline int read(){
register int x=0,t=1;
register char ch=getchar();
while('0'>ch||ch>'9'){
if(ch=='-') t=-1;
ch=getchar();
}
while('0'<=ch&&ch<='9'){
x=(x<<3)+(x<<1)+(ch^48);
ch=getchar();
}
return x*t;
}
int stack[N],top;
int main(){
int k;
k=read();
for(int i=1;i<=k;i++){
stack[i]=read();
}
for(int i=1;i<=k;i++){
while(top<stack[i]){
printf("push %d\n",++top);
}
printf("pop\n");
}
}
思路：只需了解栈的先入后出的逻辑。
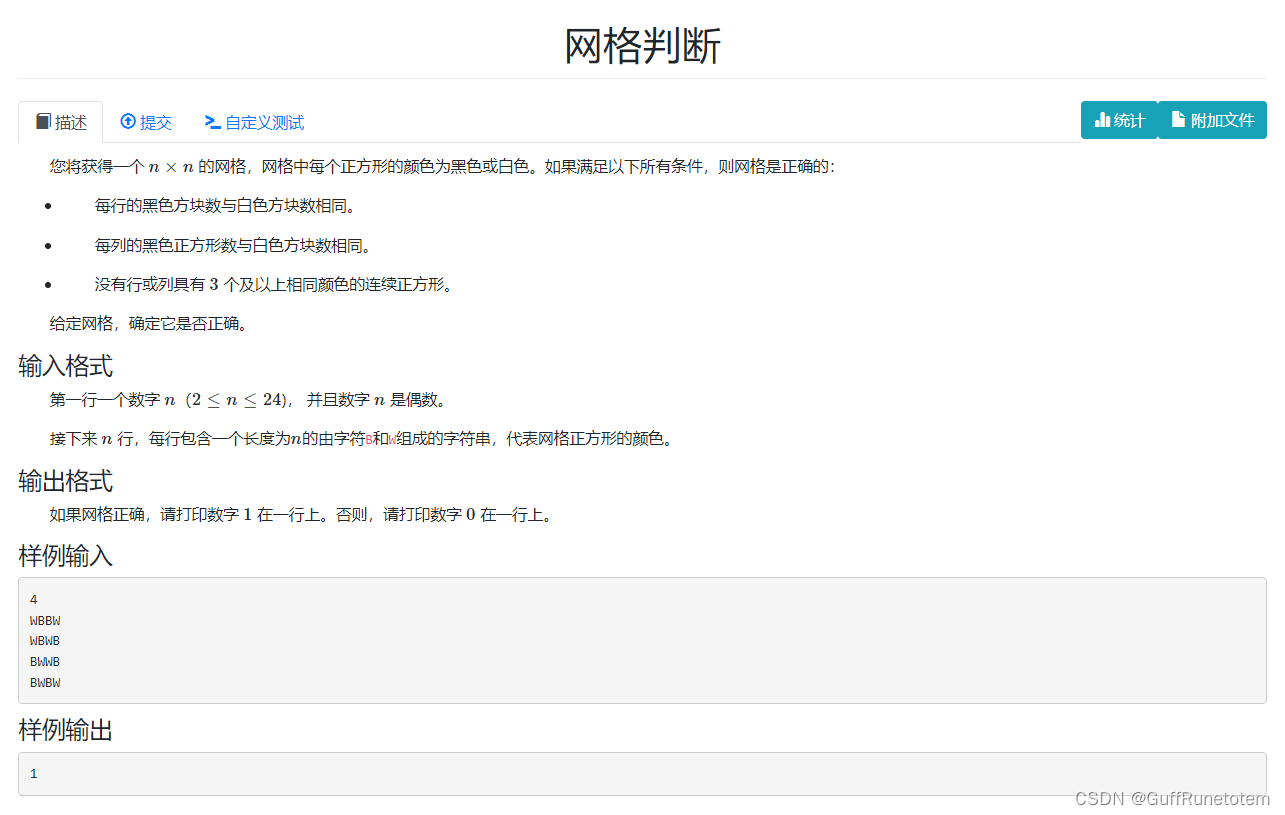
10 网格判断
#include<bits/stdc++.h>
using namespace std;
int n,tmp,cntw,cntb;
char m[25][25];
//问题出在判断连续三个上面
int main(){
ios::sync_with_stdio;
cin.tie(0);
cout.tie(0);
cin>>n;
for(int i=0;i<n;i++){
for(int j=0;j<n;j++){
cin>>m[i][j];
}
}
//行
for(int i=0;i<n;i++){
tmp=0;
cntw=0,cntb=0;
for(int j=0;j<n;j++){
if(tmp==3||tmp==-3){
cout<<0<<endl;
return 0;
}
if(m[i][j]=='W'){
cntw++;
if(m[i][j-1]=='W'){
tmp++;
}
else{
tmp=0;
tmp++;
}
}
else{
cntb++;
if(m[i][j-1]=='B'){
tmp--;
}
else{
tmp=0;
tmp--;
}
}
}
if(cntb!=cntw){
cout<<0<<endl;
return 0;
}
}
//列
for(int i=0;i<n;i++){
cntb=0,cntw=0,tmp=0;
for(int j=0;j<n;j++){
if(tmp==3||tmp==-3){
cout<<0<<endl;
return 0;
}
if(m[j][i]=='W'){
cntw++;
if(m[j-1][i]=='W'){
tmp++;
}
else{
tmp=0;
tmp++;
}
}
else{
cntb++;
if(m[j-1][i]=='B'){
tmp--;
}
else{
tmp=0;
tmp--;
}
}
}
if(cntb!=cntw){
cout<<0<<endl;
return 0;
}
}
cout<<1<<endl;
return 0;
}
思路：简单的模拟题。按行列依次判断即可。
扫一扫
809
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
