Introduction to Python Exercises 10.Scipy_scipy.optimize.nnls-优快云博客

本文链接：https://blog.youkuaiyun.com/Gosick_Geass_Gate/article/details/80573254

本文介绍了使用Python中的numpy和scipy库来解决最小二乘法问题及函数最小值问题的方法。首先利用numpy.linalg.lstsq和scipy.optimize.nnls函数求解线性最小二乘问题，并展示如何获取最小二乘解、残差等关键信息。接着使用scipy.optimize.minimize_scalar求解一维函数的最小值，并给出最大值计算示例。最后演示了如何使用scipy.spatial.distance.pdist和squareform计算并展示n维空间中对象之间的距离。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

【问题解决】

具有求解最小二乘法函数的模块有很多，下面介绍：

（1）np.linalg模块的lstsq函数（上周的11.Matplotlib习题用到）

x, residuals, rank, s = numpy.linalg.lstsq(a, b, rcond='warn')

参数：a为矩阵，b为向量。

返回值：x为最小二乘解；residuals为误差和；rank为矩阵a的秩；s为矩阵a的特征值。

（2）scipy.optimize模块的leastsq函数、least_squares函数、nnls函数和lsq_linear函数。本题目中使用scipy.optimize.nnls。

x, rnorm = scipy.optimize.nnls(A, b, maxiter=None)

参数：A为矩阵，b为向量。

返回值：x为最小二乘解；rnorm为误差的范数。

import numpy as np   
import scipy.optimize as op

m = 20
n = 10

A = np.random.random((m, n))    # 元素为[0.0, 1.0)的浮点数的20*10矩阵  
b = np.random.random(m)    # 元素元素为[0.0, 1.0)的浮点数的向量  

x, rnorm = op.nnls(A, b)
print('The least square solution x is ' + str(x[0]))
print('The norm of the residual is ' + str(rnorm))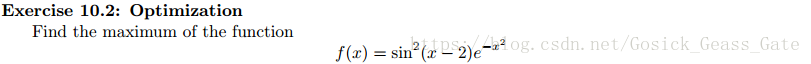

scipy.optimize模块有很多个求函数最小值的函数，本题目中使用scipy.optimize.minimize_scalar。

import scipy.optimize as op
from math import *
  
def func(x):  
    result = -pow(sin(x - 2), 2) * exp(-pow(x, 2))  
    return result  
  
res = op.minimize_scalar(func)  
  
print("The maximum = " + str(-func(res.x)))

计算n维空间中的对象两两之间距离可使用scipy.spatial.distance.pdist。

之后把向量格式的距离向量转换成一个方阵格式的距离矩阵使用scipy.spatial.distance.squareform。

import numpy as np
import scipy.spatial.distance as dis

m = 20
n = 10

X = np.random.random((m, n))	# 元素为[0.0, 1.0)的浮点数的20*10矩阵  
Y = dis.pdist(X)
Z = dis.squareform(Y)
print(Z)