KNN and K-means 监督与非监督学习

原创于 2025-12-08 15:12:01 发布 · 480 阅读

7 ·

CC 4.0 BY-SA版权

文章标签：

#kmeans #学习 #算法

深度学习专栏收录该内容

6 篇文章

订阅专栏

什么是 KNN 算法？ 🤔

KNN (K-Nearest Neighbors，K近邻算法) 是一种非参数、监督学习算法，既可用于分类，也可用于回归。它是一种惰性学习（Lazy Learning）算法，这意味着它在训练阶段几乎不做任何计算，而是将所有训练数据存储起来，直到需要做出预测时才开始计算。

它的工作原理是什么？ 💡

KNN 的核心思想是：一个样本的类别由其最近的 K 个邻居的类别决定。

1. K-近邻分类 (K-Nearest Neighbors for Classification)

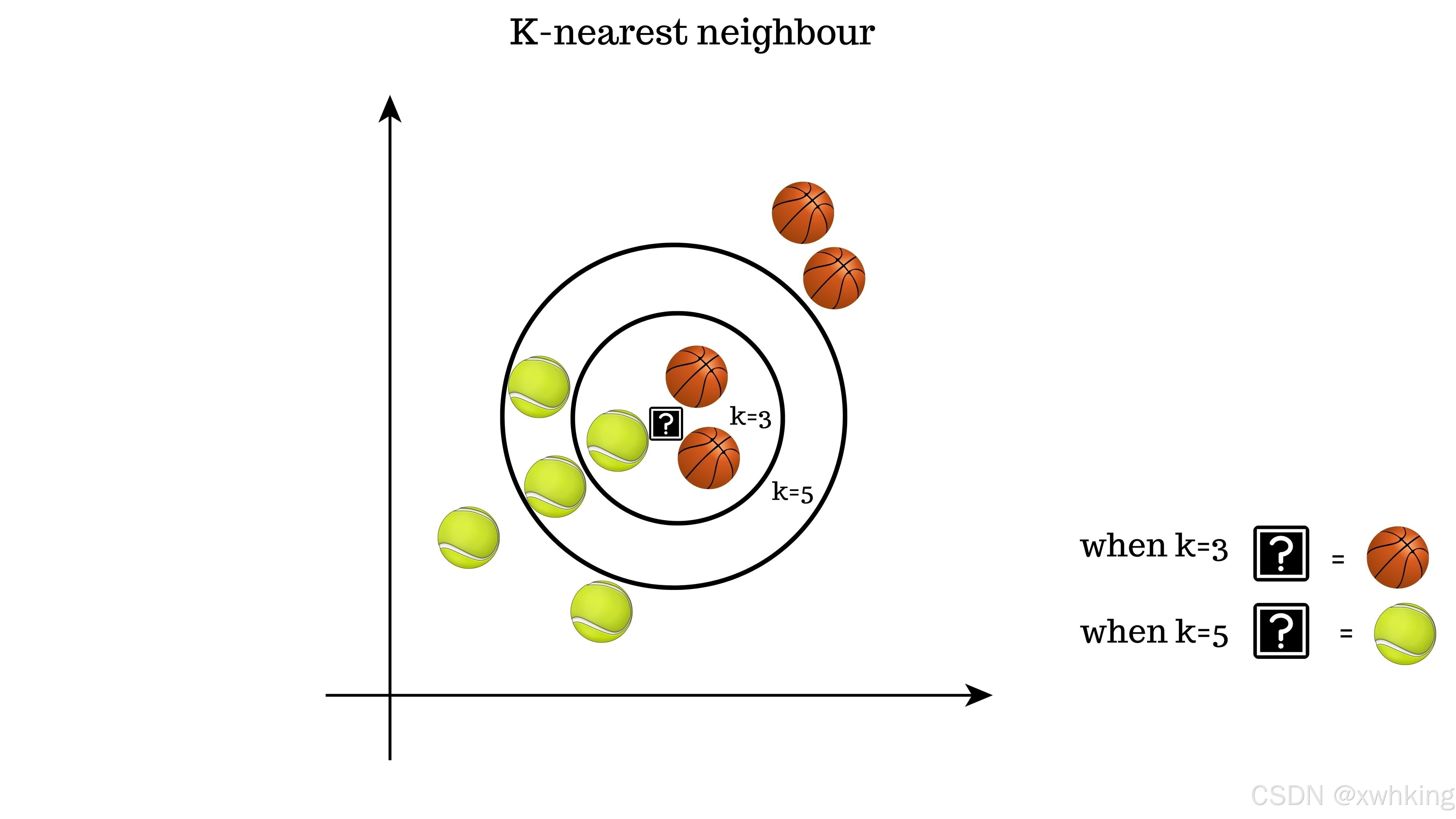
对于一个新的数据点，KNN 算法执行以下步骤来预测其类别：

确定 K 值： 选择一个正整数 K（通常较小，例如 K=3 或 K=5）。
计算距离： 计算新数据点与训练集中所有数据点之间的距离（最常见的是欧氏距离）。
找到 K 个邻居： 找出距离最近的 K 个训练样本点，这些点就是新数据点的 K 个“邻居”。
投票决定类别： 统计这 K 个邻居中，哪一类别出现的次数最多。将出现次数最多的那个类别作为新数据点的预测类别。

2. K-近邻回归 (K-Nearest Neighbors for Regression)

如果用于回归，步骤类似，但在最后一步有所不同：

找到最近的 K 个邻居。
将这 K 个邻居的目标值（即输出值）的平均值（或加权平均值）作为新数据点的预测值。

关键要素 🔑

K 值： K 的选择对结果至关重要。K 值太小（例如 K=1）容易受到异常值的影响，模型可能过于复杂（过拟合）。K 值太大会使模型过于简单，导致欠拟合，并且会模糊不同类别之间的边界。通常通过交叉验证来确定最佳 K 值。
距离度量： 用于衡量样本之间相似性的方法。最常用的是欧氏距离（Euclidean Distance）。其他包括曼哈顿距离（Manhattan Distance）或闵可夫斯基距离（Minkowski Distance）。
特征缩放： 由于 KNN 依赖于距离计算，因此所有特征应具有相似的尺度。在使用 KNN 之前，通常需要进行特征标准化或归一化。

优缺点 👍👎

在这里插入图片描述

什么是 K-Means 算法？

K-Means 算法是一种经典的无监督学习算法，主要用于聚类 (Clustering)。它的目标是将一个数据集中的 N 个数据点划分为预先设定的 K 个簇 (Cluster)，使得每个数据点都属于离它最近的聚类中心 (Centroid) 所代表的簇。

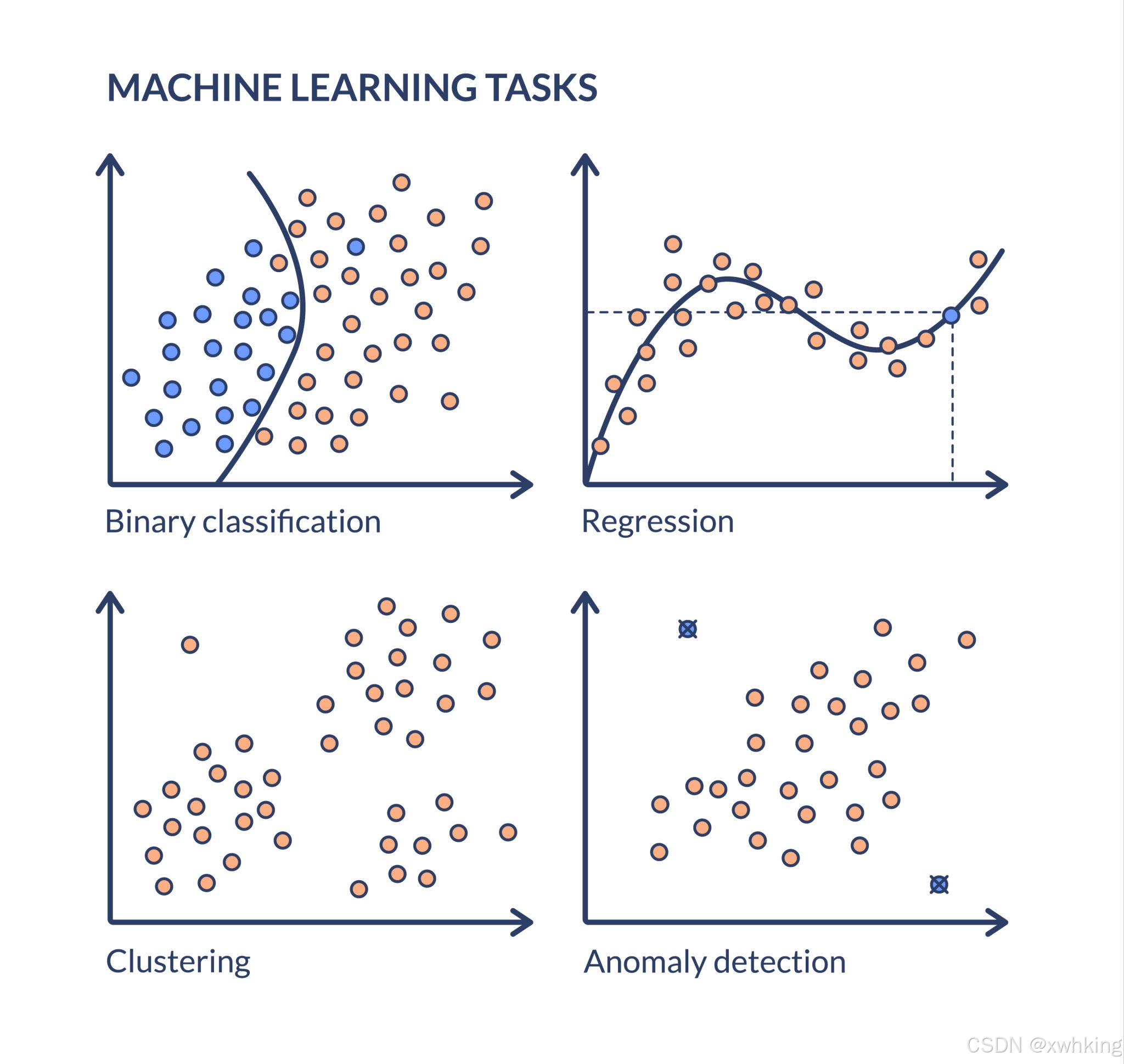
在这里插入图片描述

K-Means 的工作原理（迭代过程）

K-Means 算法通过迭代来寻找最佳的聚类划分：

初始化 (Initialization):

首先，确定要划分的簇的数量 K。
随机选择 K 个数据点作为初始聚类中心（或质心，Centroid）。

分配 (Assignment):

对于数据集中的每个数据点，计算它到 K 个聚类中心的距离（通常使用欧氏距离）。
将该数据点分配给距离它最近的那个聚类中心所在的簇。

更新 (Update):

在所有数据点都分配完毕后，重新计算每个簇的新聚类中心。新中心是该簇内所有数据点的平均值（均值，Mean）。

重复 (Repeat):

重复执行“分配”和“更新”步骤，直到聚类中心的位置不再发生显著变化，或者达到预设的最大迭代次数为止。

K-Means 与 KNN 的联系和区别 🔗

K-Means (K-Means Clustering) 和 KNN (K-Nearest Neighbors) 仅在名称和都使用距离度量（如欧氏距离）方面有相似之处，但在基本原理、目的和应用场景上存在本质区别。

📊 核心区别

在这里插入图片描述

🤝 联系

都基于距离度量： 两个算法的核心操作都是计算样本点之间的距离（最常见的是欧氏距离）来衡量相似性。
名称相似： 都包含参数 K，尽管 K 的意义完全不同。
都依赖最近邻思想： K-Means 在分配阶段是基于数据点到最近中心的距离；KNN 在预测阶段是基于数据点到最近邻居的距离。
总而言之：
如果你想将无标签的数据分成 K 个有意义的组，你应该使用 K-Means (聚类)。
如果你想根据有标签的训练数据来预测新数据的类别或数值，你应该使用 KNN (分类/回归)。

最佳实践数据集推荐：鸢尾花 (Iris) 数据集 🌸

鸢尾花数据集 (Iris Dataset) 是机器学习领域最著名、使用最广泛的数据集之一。它非常适合初学者，因为它体积小、干净，并且数据自带标签，这使得它既可以用于有监督学习（KNN）也可以用于无监督学习（K-Means 的评估）。

数据集概览

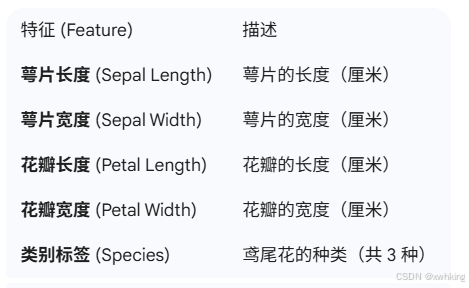
目标类别 (Labels)：

Iris Setosa (山鸢尾)
Iris Versicolour (杂色鸢尾)
Iris Virginica (维吉尼亚鸢尾)

实践代码

# 数据获取
import numpy as np
from collections import Counter
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler

# --- 欧氏距离函数 (用于两个模型) ---
def euclidean_distance(point1, point2):
    """计算两个多维点之间的欧氏距离"""
    return np.sqrt(np.sum((point1 - point2) ** 2))

# 1. 加载 Iris 数据
iris = load_iris()
X = iris.data  # 特征 (萼片/花瓣长度和宽度)
y = iris.target # 标签 (0, 1, 2 分别代表三种鸢尾花)

# 2. 特征缩放 (对距离敏感的算法是必要的)
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)


# 定义 KNN 算法
class CustomKNN:
    def __init__(self, k=3):
        self.k = k

    def fit(self, X_train, y_train):
        self.X_train = X_train
        self.y_train = y_train

    def predict(self, X_test):
        predictions = [self._predict(x) for x in X_test]
        return np.array(predictions)

    def _predict(self, x):
        distances = [euclidean_distance(x, x_train) for x_train in self.X_train]
        k_indices = np.argsort(distances)[:self.k]
        # print("1",k_indices)
        k_nearest_labels = [self.y_train[i] for i in k_indices]
        # print("2",k_nearest_labels)
        most_common = Counter(k_nearest_labels).most_common(1)
        return most_common[0][0]

#实践 KNN
# 1. 分割数据集
X_train, X_test, y_train, y_test = train_test_split(
    X_scaled, y, test_size=0.3, random_state=42
)

# 2. 初始化并训练模型 (使用 K=5)
knn_model = CustomKNN(k=5)
knn_model.fit(X_train, y_train)

# 3. 预测
y_pred = knn_model.predict(X_test)

# 4. 评估 (计算准确率)
accuracy = np.sum(y_pred == y_test) / len(y_test)
print("--- KNN 分类结果 ---")
print(f"使用的 K 值: {knn_model.k}")
print(f"测试集准确率: {accuracy:.4f}")

# 定义 K-means 算法
class CustomKMeans:
    def __init__(self, n_clusters=3, max_iter=100):
        self.n_clusters = n_clusters
        self.max_iter = max_iter
        self.centroids = None
        self.labels = None

    def _initialize_centroids(self, X):
        random_indices = np.random.choice(X.shape[0], self.n_clusters, replace=False)
        self.centroids = X[random_indices]

    def _create_clusters(self, X):
        clusters = [[] for _ in range(self.n_clusters)]
        self.labels = np.zeros(X.shape[0])

        for idx, sample in enumerate(X):
            distances = [euclidean_distance(sample, centroid) for centroid in self.centroids]
            closest_centroid_idx = np.argmin(distances)

            clusters[closest_centroid_idx].append(idx)
            self.labels[idx] = closest_centroid_idx

        return clusters

    def _update_centroids(self, X, clusters):
        new_centroids = np.zeros((self.n_clusters, X.shape[1]))
        for cluster_idx, cluster in enumerate(clusters):
            if cluster:
                cluster_points = X[cluster]
                new_centroids[cluster_idx] = np.mean(cluster_points, axis=0)
            else:
                # 处理空簇
                new_centroids[cluster_idx] = self.centroids[cluster_idx]
        return new_centroids

    def fit(self, X):
        self._initialize_centroids(X)

        for _ in range(self.max_iter):
            clusters = self._create_clusters(X)
            old_centroids = self.centroids
            self.centroids = self._update_centroids(X, clusters)

            # 检查收敛
            if np.allclose(old_centroids, self.centroids):
                break

        return self.labels
# 实践 K-means
# K-Means 在训练时不需要标签，所以使用 X_scaled
kmeans_model = CustomKMeans(n_clusters=3)
predicted_clusters = kmeans_model.fit(X_scaled)

# 评估 K-Means (与真实标签进行比较)
# 注意：由于 K-Means 的簇标签 (0, 1, 2) 顺序不一定与真实标签顺序一致，
# 简单的准确率计算不适用。我们需要使用聚类指标。

# 为了简单展示，我们打印前 10 个点的聚类结果和真实标签进行对比：
print("\n--- K-Means 聚类结果 (K=3) ---")
print("前 10 个点的预测簇标签 (K-Means):", predicted_clusters[:10].astype(int))
print("前 10 个点的真实类别标签 (Iris):", y[:10])

# 我们可以看到 K-Means 自动将数据分成了 3 组，并且与真实标签有很高的相似性。