神经网络中的网络优化和正则化（四）之正则化

转载请注明出处：https://thinkgamer.blog.youkuaiyun.com/article/details/101033364
博主微博：http://weibo.com/234654758
Github：https://github.com/thinkgamer
公众号：搜索与推荐Wiki

---

引言

神经网络中的网络优化和正则化问题介绍主要分为一，二，三，四篇进行介绍（如下所示），本篇为最后一篇主要介绍神经网络中的网络正则化。

• 第一篇包括
  • 网络优化和正则化概述
  • 优化算法介绍
• 第二篇包括
  • 参数初始化
  • 数据预处理
  • 逐层归一化
• 第三篇包括
  • 超参数优化
• 第四篇包括
  • 网络正则化

机器学习模型中的关键是泛化问题，即样本在真实数据集上的期望风险最小化，而在训练集上的经验风险最小化和期望风险并不一致。由于神经网络的拟合能力很强，其在训练集上的训练误差会降的很小，从而导致过拟合。

**正则化（Regularization）**是一类通过限制模型复杂度，从而避免过拟合，提高模型泛化能力的一种方法，包括引入一些约束规则，增加先验，提前终止等。

在传统的机器学习模型中，提高模型泛化能力的主要方法是限制模型复杂度，比如$l_1,l_2$正则，但是在训练深层神经网络时，特别是在过度参数（OverParameterized）时，$l_1,l_2$正则化不如机器学习模型中效果明显，因此会引入其他的一些方法，比如：数据增强，提前终止，丢弃法，继承法等。

$l_1,l_2$正则

$l_1,l_2$正则是机器学习中常用的正则化方法，通过约束参数的$l_1,l_2$范数来减少模型在训练数据上的过拟合现象。

通过引入$l_1,l_2$正则，优化问题变为：
$$a{\theta }^{\ast }=\underset{a}{\mathrm{argmin}}\frac{1}{N}L(y^n,f(x^n,\theta ))+\lambda l_p(\theta )$$
$L$为损失函数，$N$为训练的样本数量，$f(.)$为待学习的神经网络，$\theta$为参数，$l_p$为$l_1,l_2$正则中的一个，$\lambda$为正则项系数。

带正则化的优化问题等价于下面带约束条件的优化问题：
$$\begin{gathered} {\theta }^{\ast }=\underset{a}{\mathrm{argmin}}\frac{1}{N}L(y^n,f(x^n,\theta )) \\ subjectto{l}_p(\theta )\le 1 \end{gathered}$$

下图给出了不同范数约束条件下的最优化问题示例：

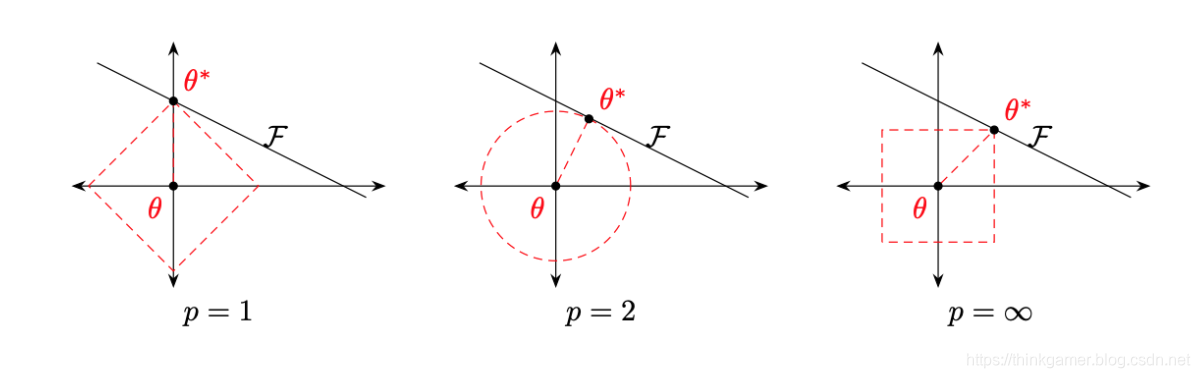
上图中红线表示$l_p$范数，黑线表示$f(\theta )$的等高线（简单起见，这里用直线表示）

从上图最左侧图可以看出，$l_1$范数的约束条件往往会使最优解位于坐标轴上，从而使用最终的参数为稀疏向量，此外$l_1$范数在零点不可导，常用下式来代替：
$$l_1(\theta )=\sum _i\sqrt{{\theta }_i^2+ϵ}$$
其中$ϵ$为一个非常小的常数。

一种折中的方法是弹性网络正则化（Elastic Net Regularization） ，同时加入$l_1,l_2$正则，如下：
$$a{\theta }^{\ast }=\underset{a}{\mathrm{argmin}}\frac{1}{N}L(y^n,f(x^n,\theta {)}_{+}{\lambda }_1{l}_1(\theta )+{\lambda }_2{l}_2(\theta )$$
其中${\lambda }_1,{\lambda }_2$分别是正则化项的参数。

权重衰减

权重衰减（Weight Deacy） 也是一种有效的正则化方法，在每次调参时，引入一个衰减系数，表示式为：
$${\theta }_t\leftarrow (1-w){\theta }_{t-1}-\alpha g_t$$
其中$g_t$为第t次更新时的梯度，$\alpha$为学习率，$w$为权重衰减系数，一般取值比较小，比如0.0005。在标准的随机梯度下降中，权重衰减和$l_2$正则达到的效果相同，因此，权重衰减在一些深度学习框架中用$l_2$正则来代替。但是在较为复杂的优化方法中，两者并不等价。

提前终止

提前终止（early stop） 对于深层神经网络而言是一种简单有效的正则化方法，由于深层神经网络拟合能力很强，比较容易在训练集上过拟合，因此在实际操作时往往产出一个和训练集独立的验证集，并用在验证集上的错误来代表期望错误，当验证集上的错误不再下降时，停止迭代。

然而在实际操作中，验证集上的错误率变化曲线并不是一条平衡的曲线，很可能是先升高再降低，因此提前停止的具体停止标准需要根据实际任务上进行优化。

丢弃法

当训练一个深层神经网络时，可以随机丢弃一部分神经元（同时丢弃其对应的连接边）来避免过拟合，这种方法称为 丢弃法（Dropout Method）。每次丢弃的神经元为随机的，对于每一个神经元都以一个概率p来判断要不要停留，对于每一个神经层 $y=f(Wx+b)$，我们可以引入一个丢弃函数$d(.)$使得$y=f(Wd(x)+b)$。丢弃函数的定义为：
$$d(x)=\{\begin{array}{c}m\odot x,WhenTrain\\ px,WhenTest\end{array}$$
其中 m ∈ { 0 , 1 } d m \in \{0,1\}^d m∈{0,1}d是丢弃掩码（dropout mask），通过以概率为p的贝努力分布随机生成，$p$可以通过一个验证集选取一个最优值，也可以设置为0.5， 这样对大部分网络和任务比较有效。在训练时，神经元的平均数量为原来的$p$倍，而在测试时，所有的神经元都可以是激活的，这会造成训练时和测试时的网络结构不一致，为了缓解这个问题，在测试时，需要将每一个神经元的输出乘以$p$，也相当于把不同的神经网络做了一个平均。

下图给出了一个网络经过dropout的示例。

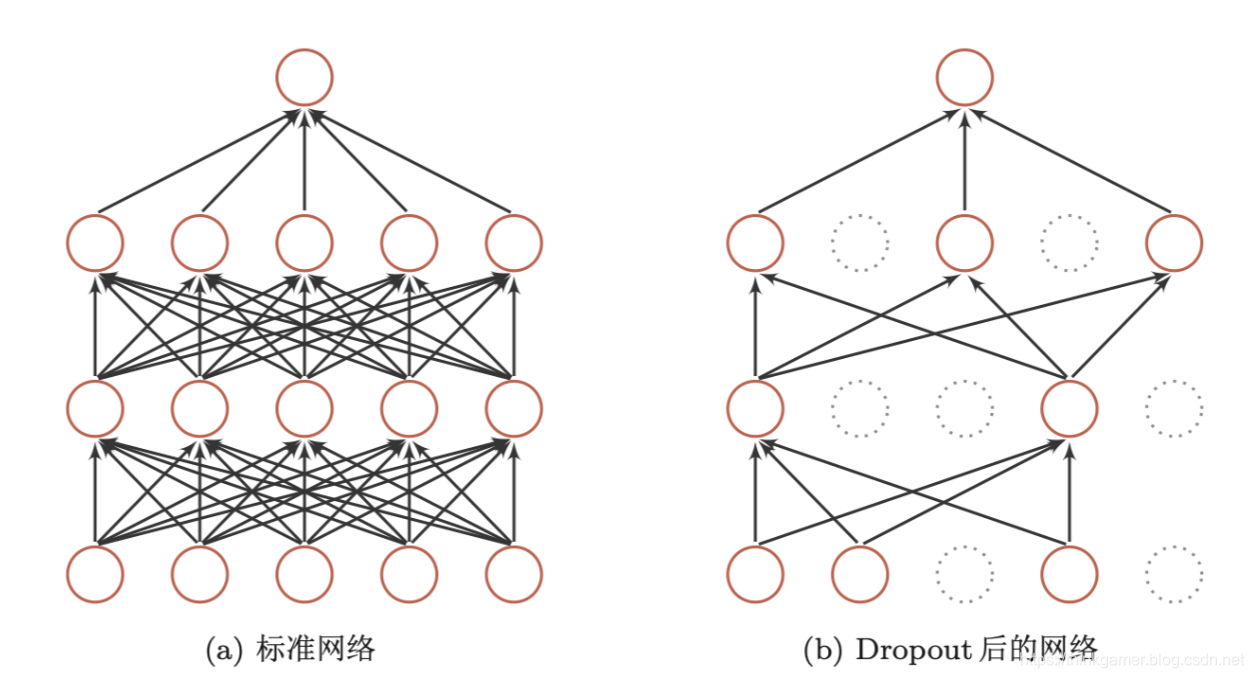
一般来讲，对于隐藏层的神经元，丢弃率$p=0.5$时最好，这样当训练时有一半的神经元是丢弃的，随机生成的网络结构具有多样性。对于输入层的神经元，其丢弃率往往设置为更接近于1的数，使得输入变化不会太大，对输入层的神经元进行丢弃时，相当于给数据增加噪声，提高网络的鲁棒性。

丢弃法一般是针对神经元进行随机丢弃，但是也可以扩展到神经元之间的连接进行随机丢弃，或每一层进行随机丢弃。

丢弃法有两种解释：

（1）集成学习的解释
每做一次丢弃，相当于从原始的网络中采样得到一个子网络，如果一个神经网络有n个神经元，那么可以采样出$2^n$个子网络，每次训练都相当于是训练一个不同的子网络，这些子网络都共享最开始的参数。那么最终的网络可以看成是集成了指数级个不同风格的组合模型。

（2）贝叶斯学习的解释

丢弃法也可以解释为一个贝叶斯学习的近似，用$y=f(x,\theta )$表示一个要学习的网络，贝叶斯学习是假设参数$\theta$为随机向量，并且先验分布为$q(\theta )$，贝叶斯方法的预测为：
$$E_{q(\theta )}[y]={\int }_{q}f(x,\theta )q(\theta )d\theta \approx \frac{1}{M}\sum _{m=1}^{M}f(x,{\theta }_m)$$
其中$f(x,{\theta }_m)$为第m次应用丢弃方法后的网络，其参数${\theta }_m$为全部参数$\theta$的一次采样。

数据增强

深层神经网络的训练需要大量的样本才能取得不错的效果，因为在数据量有限的情况下，可以通过 **数据增强（Data Augmentation）**来增加数据量，提高模型鲁棒性，避免过拟合。目前数据增强主要应用在图像数据上，在文本等其他类型的数据还没有太好的方法。

图像数据增强主要通过算法对图像进行转换，引入噪声方法增强数据的多样性，增强的方法主要有：

• 转换（Rotation）：将图像按照顺时针或者逆时针方向随机旋转一定的角度；
• 翻转（Flip）：将图像沿水平或者垂直方向随机翻转一定的角度；
• 缩放（Zoom in/out）：将图像放大或者缩小一定的比例；
• 平移（Shift）：将图像按照水平或者垂直的方法平移一定步长；
• 加噪声（Noise）：加入随机噪声。

标签平滑

在数据增强中，可以通过给样本加入随机噪声来避免过拟合，同样也可以给样本的标签引入一定的噪声。假设在训练数据集中，有一些样本的标签是被错误标注的，那么最小化这些样本上的损失函数会导致过拟合。一种改善的正则化方法是标签平滑（label smothing），即在输出标签中随机加入噪声，来避免模型过拟合。

一个样本$x$的标签一般用onehot向量表示，如下：
$$y=[0,...,0,1,.....,1{]}^T$$
这种标签可以看作硬目标（hard targets），如果使用softmax分类器并使用交叉熵损失函数，最小化损失函数会使得正确类和其他类权重差异很大。根据softmax函数的性质可以知道，如果要使得某一类的输出概率接近于1，其未归一化的得分要远大于其他类的得分，这样可能会导致其权重越来越大，并导致过拟合。i

此外如果标签是错误的，会导致严重的过拟合现象，为了改善这种情况，我们可以引入一个噪声会标签进行平滑，即假设样本以$ϵ$的概率为其他类，平滑后的标签为：
$$\tilde{y}=[\frac{ϵ}{K-1},...,\frac{ϵ}{K-1},1-ϵ,\frac{ϵ}{K-1},....,\frac{ϵ}{K-1}{]}^T$$
其中$K$为标签数量，这种标签可以看作是软目标（soft targets）。标签平滑可以避免模型的输出过拟合到硬目标上，并且通常不会降低其分类能力。

上边的标签平滑方法是给其他$K-1$个标签相同的概率$\frac{ϵ}{K-1}$，没有考虑目标之间的相关性。一种更好的做法是按照类别相关性来赋予其他标签不同的概率，比如先训练另外一个更复杂的教师网络，并使用大网络的输出作为软目标进行训练学生网络，这种方法也称为知识精炼（Knowledge Distillation）。

总结

至此，神经网络中的网络优化和正则化（一）（二）（三）（四）篇已经完成，如下：

• 神经网络中的网络优化和正则化（一）之学习率衰减和动态梯度方向
• 神经网络中的网络优化和正则化（二）之参数初始化/数据预处理/逐层归一化
• 神经网络中的网络优化和正则化（三）之超参数优化
• 神经网络中的网络优化和正则化（四）之正则化

神经网络中的网络优化和正则化即是对立又统一的关系，一方面我们希望找到一个最优解使得模型误差最小，另一方面又不希望得到一个最优解，可能陷入过拟合。优化和正则化的目标是期望风险最小化。

目前在深层神经网络中泛化能力还没有很好的理论支持，在传统的机器学习上比较有效的$l_1,l_2$正则化在深层神经网络中作用也比较有限，而一些经验性的做法，比如随机梯度下降和提前终止，会更加有效。

---

【技术服务】，详情点击查看： https://mp.weixin.qq.com/s/PtX9ukKRBmazAWARprGIAg

---

扫一扫 关注微信公众号！号主 专注于搜索和推荐系统，尝试使用算法去更好的服务于用户，包括但不局限于机器学习，深度学习，强化学习，自然语言理解，知识图谱，还不定时分享技术，资料，思考等文章！

---