数论（总）

一.数学原理

一.计数原理

常见原理/定理

加法原理：分类

乘法原理：分步

二项式定理：

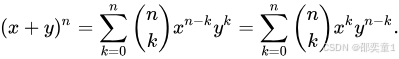
容斥定理：

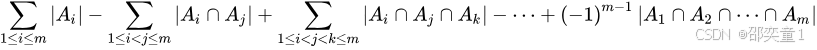
唯一分解原理：

任何数都可以分成质因数的幂的相乘

扩展性质：

一个数可以被x整除，则这个数至少存在一个质因数的幂<x在该质因数的幂
 

常见恒等式

常见计数模型

环形排列：

n个元素环形摆放有（n-1）！排列

（有n次是重复的）

错位排序：

每个数不在自己原本的位置上

有n!*(1-1+1/2!+1/3!.....+(-1)^n/n!)种排列
（利用容斥定理，计算所有非错位排列的个数）

卡特兰数：

h(n) = C(2n, n) / (n + 1) = C(2n, n) - C(2n, n - 1)

应用场景‌：

计算所有出栈排列数

计算所有合理的括号排列数

常见计数方法

插空法：解决相同元素分组问题

基本形式：

1.n个相同元素，不同个m组，每组至少有一个元素；则只需在 n 个元素的n-1 个间隙中放置 m-1 块隔板把它隔成 m 份，求共有多少种不同方法？

其解题思路为：将 n 个相同的元素排成一行， n 个元素之间出现了（ n-1 ）个空档，现在我们用（ m-1 ）个 “档板 ”插入（ n-1 ）个空档中，就把 n 个元素隔成有序的 m 份。

2.有 n 个相同的元素，要求分到 m 组中，问有多少种不同的分法？

解题思路：这种问题是允许有些组中分到的元素为 “0”，也就是组中可以为空。将每组都填上 1 个，这样所要元素总数就 m 个，问题也就是转变成将（ n+m ）个元素分到 m 组。

数学形式：

a0+a1+a2……+an==k

ai>=1，对应每组分至少一个

ai>=0，对应组中可以为空

二.常见算法

一.求最大公约数

辗转相除法

int gcd(int a,int b){
    if(a%b==0){
        return b;
    }else{
        return gcd(b,a%b);
    }
}

二.裴蜀定理与扩展欧几里得算法

裴蜀定理：

总存在整数x，y使 ax+by=gcd(a，b) 成立。

证明方法就是辗转相除法逆过来。

裴蜀定理的推论：

1.a，b最大公约数的另一种理解方法是：找到一组整数x，y使 ax+by 得到最小正数解。

2.假如方程 ax+by=c 有整数解，则c一定是gcd(a，b)的倍数。

3.可扩展到多项式。

扩展欧几里得算法：

寻找 ax+by=gcd(a，b) 的一个解。

原理（公式推导）：

设g为最大公约数，gcd调用时，第k次输入的参数为a[k],b[k];

在最后一次调用中，g=x*a[n]+y*b[n]。

(实际上最后一次x==1，y==0)

则可推导上一次调用时的x，y：g=x*b[n-1]+y*((a[n-1]-(a[n-1]/b[n-1])*b[n-1])

(a[n]对应b[n-1]，b[n]对应(a[n-1]/b[n-1])*b[n-1]，即a%b)

整理得：

g = y*a[n-1] + (x-y*(a[n-1]/b[n-1]))*b[n-1];

这样一直推到初始的两个a，b，就得出一个解x，y。

代码：

int a,b,x,y,g;

void exgcd(int a,int b){
    if(b==0){
        g=a;
        x=1;
        y=0;
    }else{
        exgcd(b,a%b);
        int px=x,py=y;
        x=py;
        y=px-py*(a/b);
    }
}