【seaborn】kdeplot用法 & 核密度估计（KDE）原理介绍

核密度估计(Kernel Density Estimation)

定义

核密度估计是估计随机变量的概率密度函数的非参数方法，即一种针对连续数据的密度估计方法，并且其根据数据本身的相互关系得到，无需对数据分布做假设。
假设样本彼此独立并遵循相同的分布。给定带宽H，每个样本都由平滑的核函数拟合。某数据的密度值可以视为其他所有样本对该数据的平均影响。
$${\hat{f}}_h(x)=\frac{1}{n}\sum _{i=1}^n{K}_h\left(x-x_i\right)=\frac{1}{nh}\sum _{i=1}^{n}K\left(\frac{x-x_i}{h}\right)$$
其中K是内核（一个非负函数），而h > 0是一个称为bandwidth的平滑参数。下标为h的内核称为缩放内核，定义为$K_h(x)=1/hK(x/h)$。直观地讲，我们希望选择h尽可能小，以使数据能够容纳；但是，在估算器的偏差与其方差之间始终存在取舍。
核估计方法产生的函数具有以下特点：

1. 归一性：表达式满足${\int }_{-\infty }^{+\infty }K(x)dx=1$
2. 非负性：表达式满足$K(x)\ge 0$
3. 对称性：表达式满足$K(x)-K(-x)=0$
   通常使用一系列核函数：均匀函数，三角函数，双权重函数，三重函数，Epanechnikov函数，法线函数和其他函数。
   $f_h(x)$可以表示每个样本点对总体分布造成的影响

例子

以上表述可能还是比较难以理解，参考维基百科上的间的例子，如果之前对RBF和SVM中的核概念比较熟悉的话，应该很容易理解。尤其径向基RBF思想基本相似
如下最简单的六个样本点数据分别作直方图和核密度估计

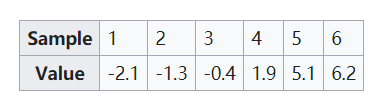
对于直方图，首先将水平轴划分为子区间或覆盖数据范围的区间：在这种情况下，每个区间的宽度为2，共6个区间。每当一个数据点落入此区间时，高度为1 /12（概率密度：1/（样本点*面积））。如果同一数据仓中有多个数据点，则这些框会堆叠在一起。
对于核密度估计，将标准偏差为2.25（用红色虚线表示）的正太分布核放置在每个数据点上。对内核进行求和以得出核密度估计（蓝色实线）。核密度估计的平滑度（与直方图的离散度相比）说明了对于连续随机变量，核密度估计如何更快地收敛到真实的基础密度。

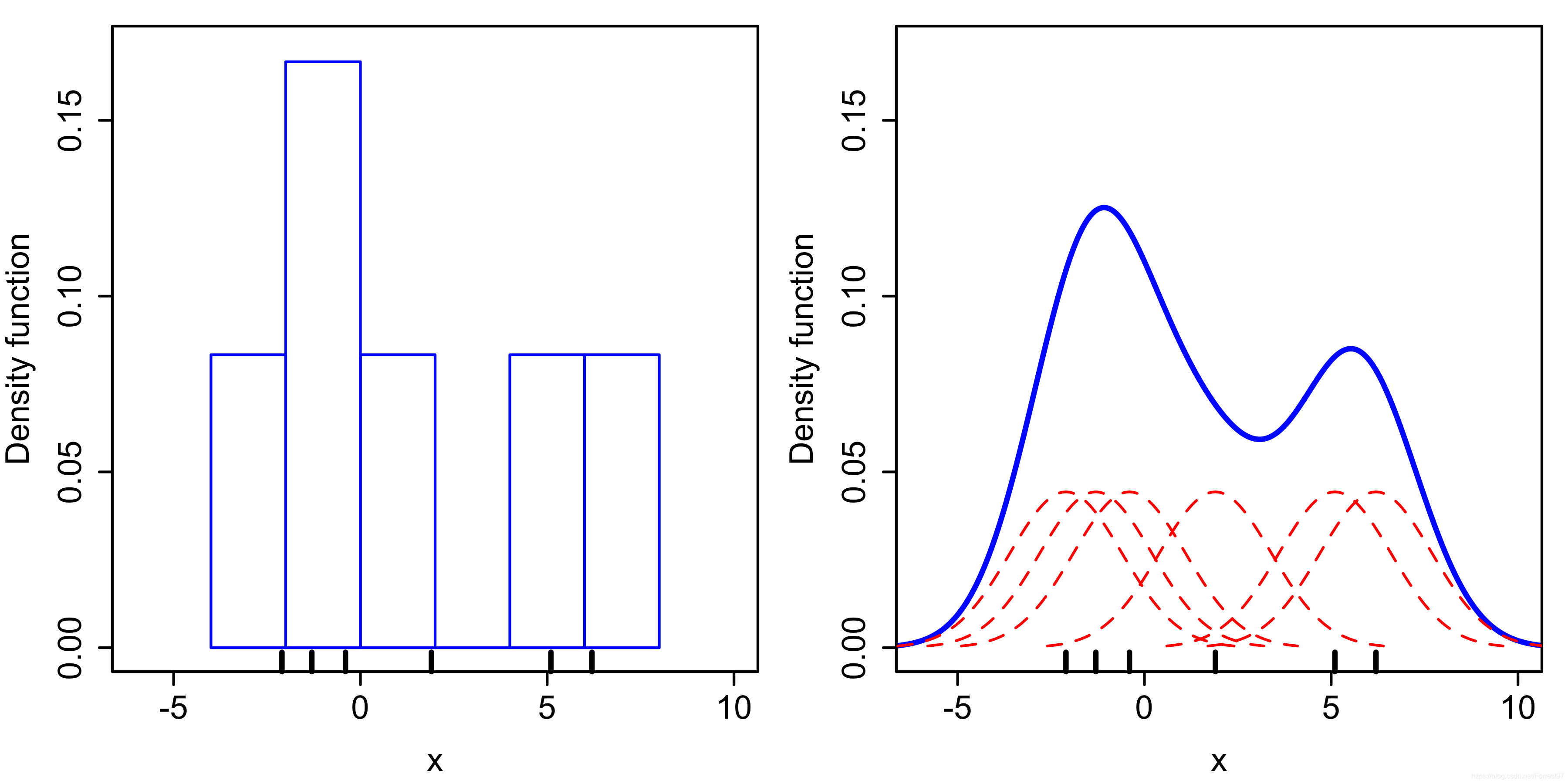
带宽（bandwidth）参数选择

试验证明了核函数类型的选择对核密度估计的影响不是很大，其概率密度函数的拟合效果主要受带宽 h 的影响，一般 h 越大，拟合的曲线会越光滑，h 选择过小，曲线越粗糙。
研究的方法，可以通过交叉验证法（一种通过样本来计算带宽的方法），该方法使用积分平方误差作为选择带宽的评价指标，详见参考。
经验表达式

$h={\left(\frac{4{\hat{\sigma }}^5}{3n}\right)}^{\frac{1}{5}}\approx 1.06\hat{\sigma }{n}^{-1/5}$
$\sigma$ 为样本的标准差，$n$ 为样本个数

参考

https://en.wikipedia.org/wiki/Kernel_density_estimation
https://blog.youkuaiyun.com/unixtch/article/details/78556499
https://www.zhihu.com/question/27301358

seaborn.kdeplot

seaborn提供了十分方便的API可以直接实现核密度估计，具体共性的形参介绍我就不赘述了。

这里重点说说核，带宽相关的参数
核参数默认为高斯核，且0.11.0以后的版本非高斯核并不再支持，这也与上面讨论的核对结果影响不大的结论一致。

• kernel: Deprecated since version 0.11.0: support for non-Gaussian kernels has been removed.

带宽相关的参数包括bw和bw_adjust。其中bw的参数，默认 采用上述经验公式得到，但是如果发现曲线还是不够平滑时，可以增大bw_adjust，即对bw乘以一个系数。
cut,clip是用于限制概率分布超过了有效区间。

• bw：str, number, or callableSmoothing parameter.
• bw_adjust: Factor that multiplicatively scales the value chosen using bw_method. Increasing will make the curve smoother
• cut: number, optionalFactor, multiplied by the smoothing bandwidth, that determines how far the evaluation grid extends past the extreme datapoints. When set to 0, truncate the curve at the data limits. 根据原有数据范围确定分布区间
• clip: pair of numbers None, or a pair of such pairs. Do not evaluate the density outside of these limits. 只考虑某区间内的数据

tips = sns.load_dataset("tips")
sns.kdeplot(data=tips, x="total_bill")
sns.kdeplot(data=tips, x="total_bill", bw_adjust=.2)
sns.kdeplot(data=tips, x="total_bill", bw_adjust=5, cut=0)

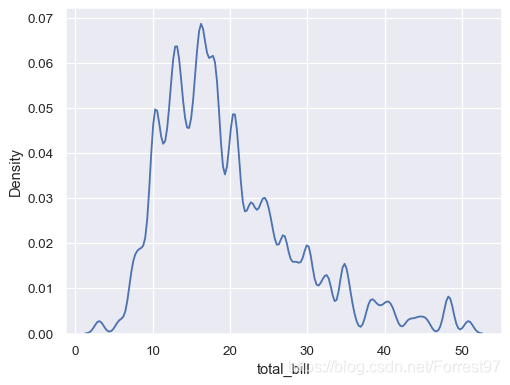
比如bw_adjust=.2时，曲线保留更多特征，但是明显不够光滑

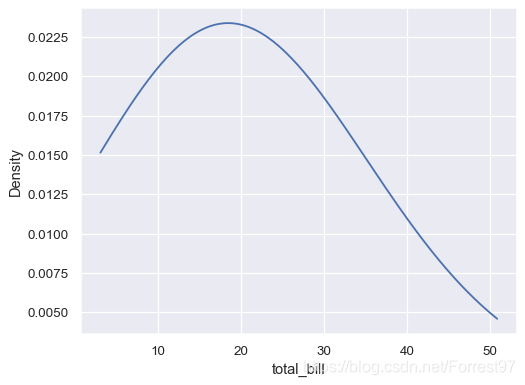
而当bw_adjust=5时，曲线明显平滑了很多

http://seaborn.pydata.org/generated/seaborn.kdeplot.html