上一讲主要讲的是传统的语言模型到神经语言模型的过渡,其中涉及的是标准RNN,包括它的构成以及在多种NLP任务上的应用。
RNN虽然作为一种神经语言模型相比于传统的模型具有一定的优势,但是它仍然存在着一系列的问题,比如:
- 序列进行,计算困难
- 难以捕捉长程依赖
另外一个大问题便是梯度消失,这一讲更加详细的来了解标准RNN中的梯度消失问题,并介绍RNN的几个变体,包括:
- LSTM
- GRU
- Bidirectional RNNs
- Multi-layer RNNs

首先来看梯度消失问题,当我们按照上一讲的方式设定损失函数后,在反向传播的过程中,如果要更新 h ( 1 ) h^{(1)} h(1),那么需要计算 ∂ J ( 4 ) ∂ h ( 1 ) \frac{\partial J^{(4)}}{\partial h^{(1)}} ∂h(1)∂J(4)。而根据链式法则,我们计算其他部分才能得到最后的结果
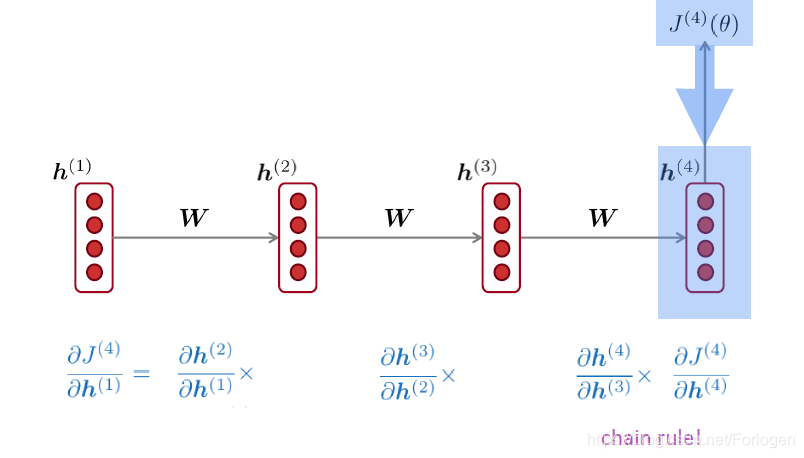
如果中间的计算结果越来越小时,那么在反向传播的过程中导致传到 h ( 1 ) h^{(1)} h(1)的梯度信息就会极其小,甚至出现梯度消失的严重问题。这是由于模型无法得到梯度信息,也就无法更新权重参数,整个模型就无法继续训练了。
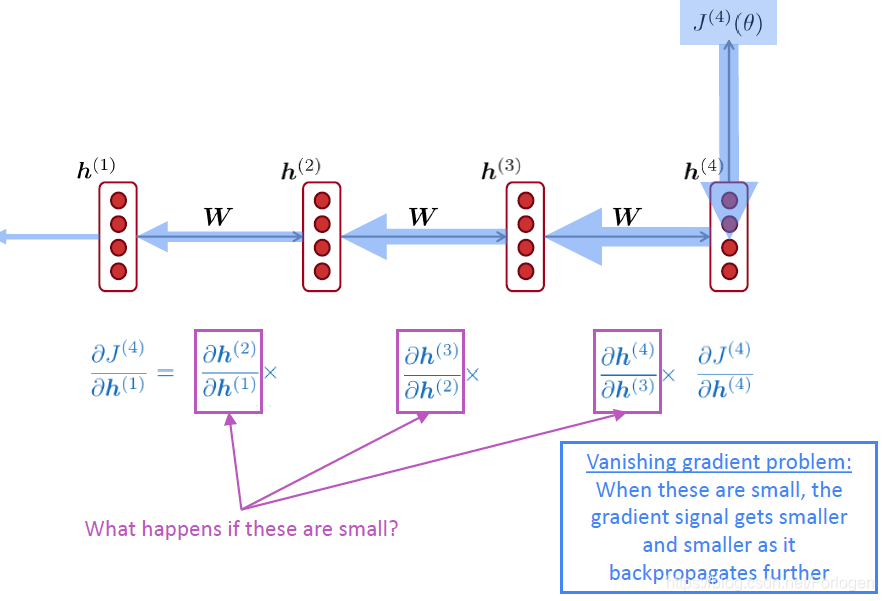
回顾上一讲的内容,中间隐状态的计算为 h ( t ) = σ ( W h h ( t − 1 ) + W x x ( t ) + b 1 ) \boldsymbol{h}^{(t)}=\sigma\left(\boldsymbol{W}_{h} \boldsymbol{h}^{(t-1)}+\boldsymbol{W}_{x} \boldsymbol{x}^{(t)}+\boldsymbol{b}_{1}\right) h(t)=σ(Whh(t−1)+Wxx(t)+b1),根据链式法则,微分计算公式为 ∂ h ( t ) ∂ h ( t − 1 ) = diag ( σ ′ ( W h h ( t − 1 ) + W x x ( t ) + b 1 ) ) W h \frac{\partial \boldsymbol{h}^{(t)}}{\partial \boldsymbol{h}^{(t-1)}}=\operatorname{diag}\left(\sigma^{\prime}\left(\boldsymbol{W}_{h} \boldsymbol{h}^{(t-1)}+\boldsymbol{W}_{x} \boldsymbol{x}^{(t)}+\boldsymbol{b}_{1}\right)\right) \boldsymbol{W}_{h} ∂h(t−1)∂h(t)=diag(σ′(Whh(t−1)+Wxx(t)+b1))Wh
考虑下面的情况,在时间步 t t t时 J ( i ) ( θ ) J^{(i)}(\theta) J(i)(θ)对 h ( j ) h^{(j)} h(j)求偏微分,如果图中紫框部分的 W h W_{h} Wh很小时,在往前传播的过程中,这一项就可能会消失,导致梯度无法继续计算,出现梯度消失问题。

考虑上式的 L 2 L_{2} L2范数有如下的形式 ∥ ∂ J ( i ) ( θ ) ∂ h ( j ) ∥ ≤ ∥ ∂ J ( i ) ( θ ) ∂ h ( i ) ∥ ∥ W h ∥ ( i − j ) ∏ j < t ≤ i ∥ diag ( σ ′ ( W h h ( t − 1 ) + W x x ( t ) + b 1 ) ) ∥ \left\|\frac{\partial J^{(i)}(\theta)}{\partial \boldsymbol{h}^{(j)}}\right\| \leq\left\|\frac{\partial J^{(i)}(\theta)}{\partial \boldsymbol{h}^{(i)}}\right\|\left\|\boldsymbol{W}_{h}\right\|^{(i-j)} \prod_{j<t \leq i}\left\|\operatorname{diag}\left(\sigma^{\prime}\left(\boldsymbol{W}_{h} \boldsymbol{h}^{(t-1)}+\boldsymbol{W}_{x} \boldsymbol{x}^{(t)}+\boldsymbol{b}_{1}\right)\right)\right\| ∥∥∥∥∂h(j)∂J(i)(θ)∥∥∥∥≤∥∥∥∥∂h(i)∂J(i)(θ)∥∥∥∥∥Wh∥(i−j)j<t≤i∏∥∥∥diag(σ′(Whh(t−1)+Wxx(t)+b1))∥∥∥
对于上式而言,Pascanu等人证明当 W h W_{h} Wh最大的特征值小于1时,左边的梯度将指数级的缩小;当最大的特征值大于1时,梯度值反过来就会增大。
在BP的过程中,参数的更新更多的依赖于靠近它的部分,而不是远离它的部分。也就是说它无法捕捉到远离它的项所带给它的影响。如下图所示,当更新 h ( 1 ) h^{(1)} h(1)时, J ( 2 ) ( θ ) J^{(2)}(\theta) J(2)(θ)相比于 J ( 4 ) ( θ ) J^{(4)}(\theta) J(4)(θ)所提供的梯度信息显然更大。
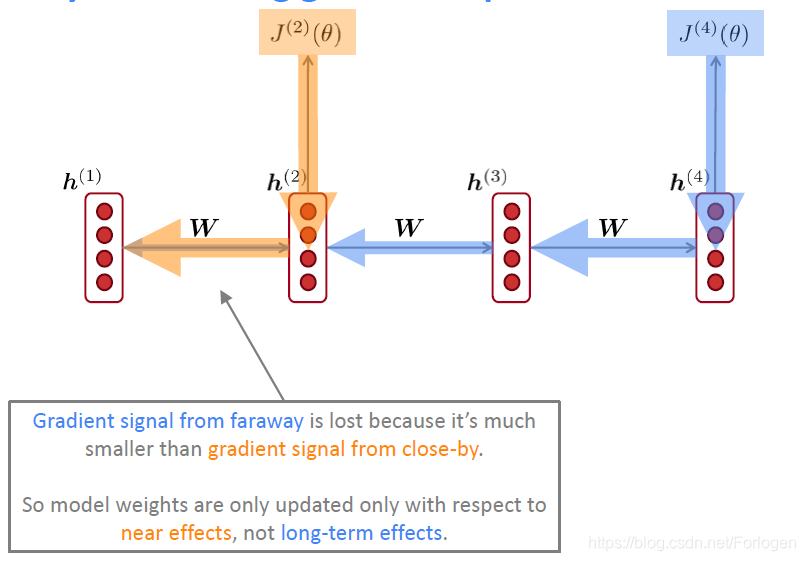
我们还可以将梯度看做是过去的状态对于将来影响的一种度量,如果在长程问题中出现梯度消失,那么在更新当前的参数时就无法依赖于 t t t到 t + n t+n t+n时间步的信息,或者说我们使用 t t t到 t + n t+n t+n时间步的信息更新得到的参数是不正确的。
那么梯度消失对于基于RNN的语言模型有什么影响呢?假设我们需要根据下面的文本预测横线上缺失的词,对于人来说,我们可以很容易的判断出应该是tickets

但是对于RNN模型来说,模型只有捕捉到了tickets和第7时间步的词的依赖关系时,他才能最后得到正确的结果。一旦在BP的过程中梯度信息消失了,模型就无法学习到这种依赖关系,即它无法得到正确的结果。
而对于梯度爆炸来说,当在SGD更新的过程中梯度信息很大时,使得更新过程中“迈的步子太大”,导致最新模型难以收敛
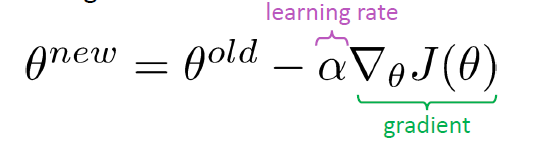
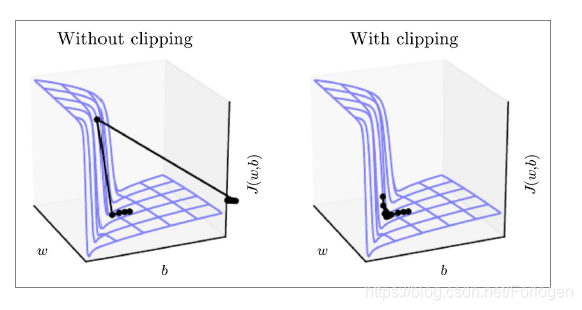
解决梯度爆炸一种经典的方法表示梯度裁剪(gradient clipping):如果梯度的范数大于设定的阈值时,在SGD更新过程中就对它放缩到合适的区间中,算法的伪代码如下:

假如 w w w和 b b b都是标量时,RNN的损失面简单如下所示。在更新的过程中,本来应该是一小步一小步的进行更新,当位于"墙"下时,更新过程应该逐步的往上,但是梯度可能会爆炸到非常大,指向一个奇怪的方向。而当我们使用了gradient clipping时就可以避免这种现象的发生,效果如右图所示。
如何解决梯度消失问题呢?这个问题可以理解为RNN无法在经过多个时间步后仍然很好的保留之前的信息,那么如果额外的添加一个记忆单元来存储这些信息,模型是否就可以较好的捕捉这种长程依赖呢?
这就是下面所要介绍的LSTM(Long Short-Term Memory)和GRU(Gated Recurrent Units)。LSTM是Schmidhuber在1997年提出的解决RNN中梯度消失问题的一种变体,每个时间步不仅有标准RNN的隐状态 h t h^{t} ht,同时还有记忆状态 c ( t ) c^{(t)} c(t),它负责存储长期依赖信息

LSTM单元如下所示
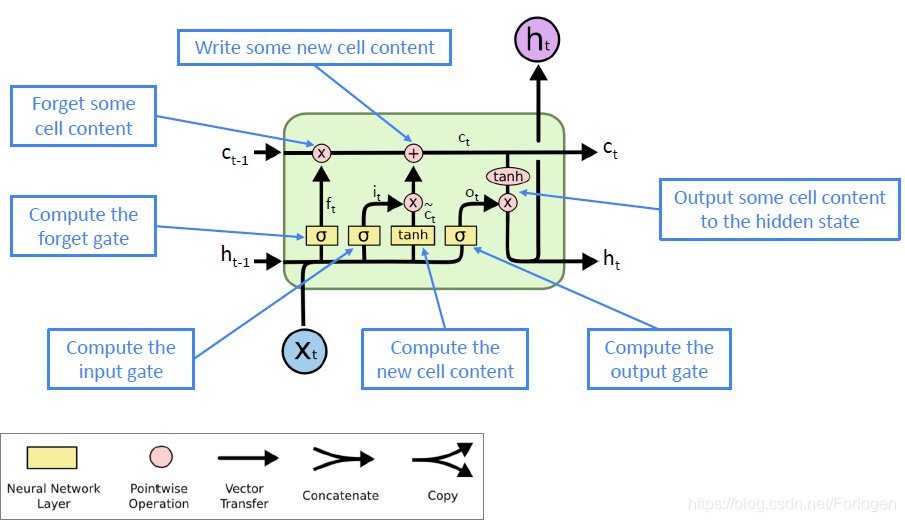
LSTM涉及的数学表达如下所示
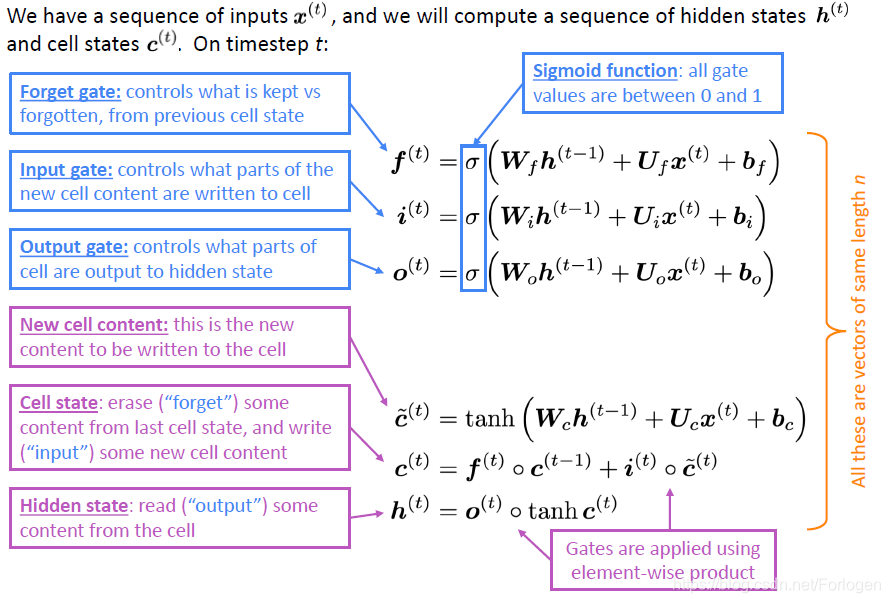
关于LSTM之前写过一篇简单的介绍:循环神经网络初始,更详细的介绍可见Understanding LSTM Networks。
LSTM是如何解决梯度消失问题的呢?简单来说,由于LSTM引入了门机制,它相比于RNN可以更好的保留多个时间步的信息。例如如果设置遗忘门去记住每个时间步的信息,那么记忆单元就可以无限存储之前的信息,当然这这是理论上的假设。虽然LSTM可以在一定程度上缓解梯度消失的出现,但它并不能保证梯度消失完全不会出现。只不过它提供了一种模型架构,使得既可以很好的避免梯度消失,又可以较好的保留长程依赖。
在Transformer出现之前,LSTM在序列数据处理方面发挥着重要的作用,在NLP领域LSTM也是很多情况下模型的首选。但最近Transformer和BERT等一系列强大的预训练模型的出现,使得LSTM并不那么耀眼了。

GRU是相对LSTM更简单的一种RNN的变体,它只有更新门(Update gate)和重置门(Reset gate)
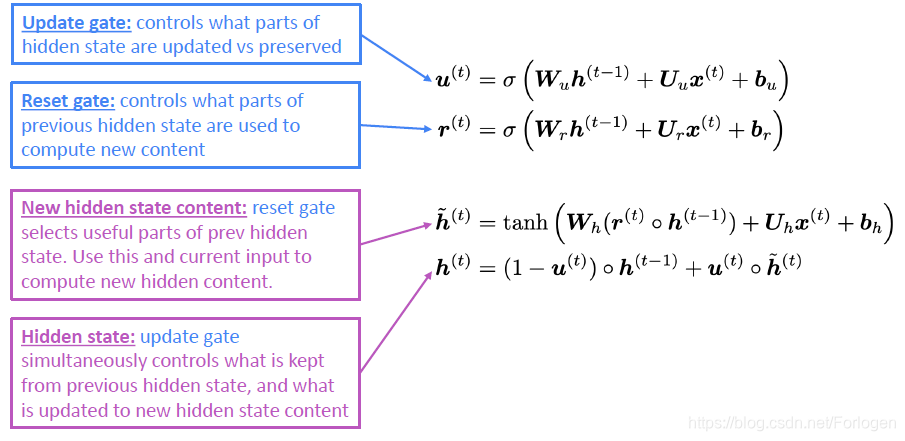
当然RNN还有很多其他的变体,而LSTM和GRU是最被广泛使用的两种形式。但是两者之间的效果并没有绝对的差别,往往在不同的任务上可以发挥各自的优势,可能最大的不同之处在于GRU的参数更少,更容易计算。在实际的使用中,通常将LSTM作为默认的选择,如果模型的效果可以达到预期有希望计算效率更高的话,可以再转到GRU上。
另外需要注意的是,梯度消失和梯度爆炸并不只是RNN中存在的问题。它同样存在于前馈神经网络和卷积神经网络中,尤其是当网络越深时,问题越严重。为了很好的解决这个问题,不同的研究人员纷纷提出了不同的网络架构方案,例如
-
ResNet

-
DenseNet

-
Highwaynet

更详细的内容参见原始论文
Highway Networks
Densely Connected Convolutional Networks
Deep Residual Learning for Image Recognition
除了LSTM、GRU还介绍了双向RNN(Bidirectional RNNs),如下所示,它将从左到右和从右到左的结果拼接起来作为最后的隐状态。
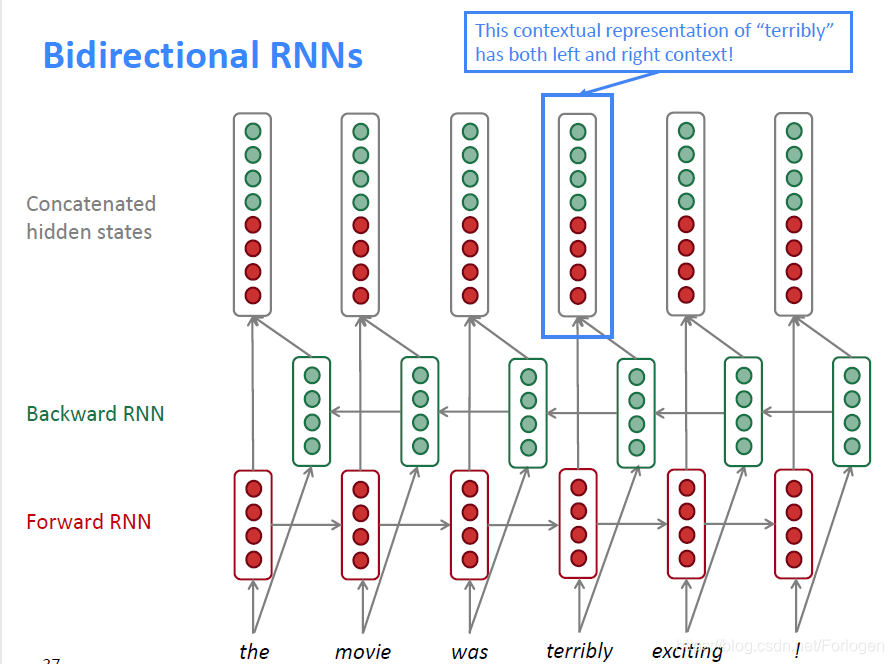
时间步 t t t的数学表示

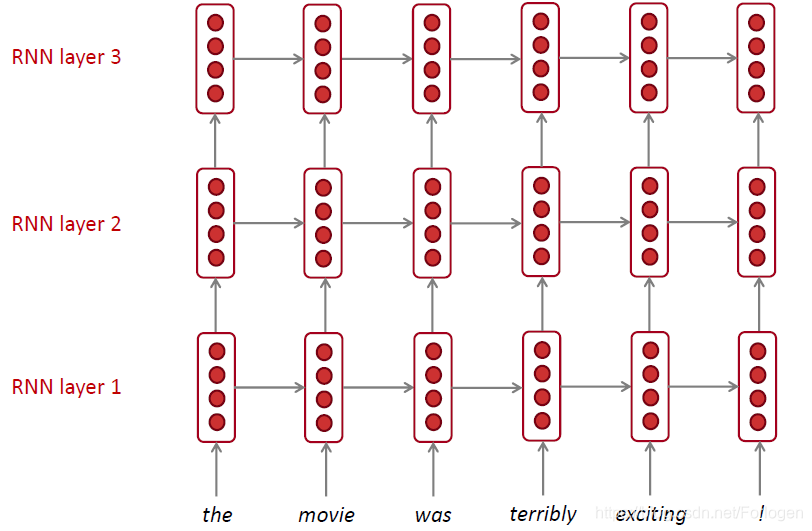
RNN 同样也可以做的很深,这便是Multi-layer RNNs,,它支持捕捉到更加复杂的特征
总结:这一将主要介绍了RNN中的梯度消失和梯度爆炸问题和相应的解决方法,最后介绍了RNN的四种形式的变体LSTM、GRU、Bidrectional RNNs和Multi-layer RNNs。
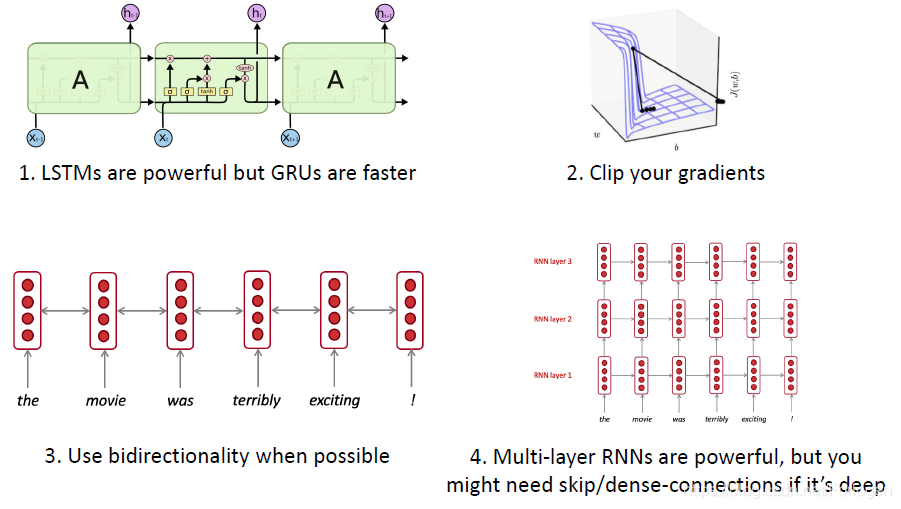
 RNN的挑战与解决方案
RNN的挑战与解决方案







 本文深入探讨了RNN在处理序列数据时遇到的梯度消失与爆炸问题,阐述了LSTM、GRU等变体如何通过引入门控机制解决这些问题,以及双向RNN和多层RNN如何增强模型能力。
本文深入探讨了RNN在处理序列数据时遇到的梯度消失与爆炸问题,阐述了LSTM、GRU等变体如何通过引入门控机制解决这些问题,以及双向RNN和多层RNN如何增强模型能力。
















 812
812

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








