循环神经网络初识

最新推荐文章于 2025-06-12 18:07:03 发布
最新推荐文章于 2025-06-12 18:07:03 发布
阅读量1.4k 收藏 2
点赞数 1
CC 4.0 BY-SA版权
分类专栏： Deep Learning
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/Forlogen/article/details/89853130
本文介绍了循环神经网络（RNN）。传统前馈神经网络无法持续思考，存在诸多不足，而RNN具有短期记忆能力，能处理任意长度序列。但RNN在时间维度深时会出现梯度问题，LSTM作为其变体可有效解决。此外，还列举了RNN的多种应用场景。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

如何理解RNN？

当我们在面对一个新的问题时，我们总是会从头脑中搜索类似的问题的解决方案，看有什么可以借鉴的地方，而不是蒙头从零开始思考。同样的在阅读一篇文章时，如果想理解某一句话，我们可能需要看前面的几个词和后面的几个词，如果想要理解一段话，还可能需要结合上下文。人类这样的思维过程显示了我们的思考是一个持续的过程，某时刻的想法要依赖于前面所学得的东西。而深度学习中传统的前馈神经网络是做不到持续思考的，它具有如下的不足之处：

  • 节点之间的而连接存在于前一层和后一层之间，同层的节点之间是没有连接的，也就是说同层节点间是无循环的
  • 输入和输出的维数是固定的，不能任意的改变
  • 无法处理边长的序列数据，例如语句、语音信号等
  • 它基于假设每次输入都是独立的，即每一次网络的输出只依赖于当前的输入，与它之前、之后网络的输入都无关

例如下图是一个包含输入层、一个隐藏层和输出层的简单的前馈神经网络


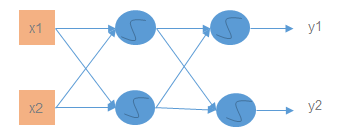
在这里插入图片描述

那么如何理解前馈神经网络无法做到持续思考的不足呢？下面我们用一个例子来看一下，如下图所示，我们有两个句子，唯一的不同之处在于Beijing前面的单词是不同的，这就导致了两句话表达的意思就完全是不同的。当我们将两个句子单独的输入到前馈神经网络中，我们希望网络可以做的的是：根据对于句子的理解，将第一个句子中的Beijing标注为destination，将第二个句子中的Beijing标注为place of departure


在这里插入图片描述

但是对于传统的前馈神经网络，这样的要求似乎有点强人所难了，因为它没有记忆呀！如果我们希望相同的词在不同的句子中可以被正确的区分所表达的不同的含义，前馈神经网络就无法满足要求了，这时就需要使用循环神经网络。

循环神经网络（Recurrent Neural Network，RNN）是一种具有短期记忆能力的神经网络，神经元不仅可以接受其他神经元的信息，也可以接收自身的信息，形成了一种具有环路的结构。它相比于前面的前馈神经网络具有如下的优势：

  • 通过使用带自反馈的神经元，能够处理任意长度的序列
  • 更加符合生物神经网络的结构

一个简单的的前向循环神经网络如下所示，它在基本的结构上多了一个记忆单元（memory cell），它可以存储当前的输出，将其作为下一个时刻网络的输入。这样的话，当我们分析当前的输入时，就可以结合前面输入的信息进行分析，解决了输入之间的依赖问题。


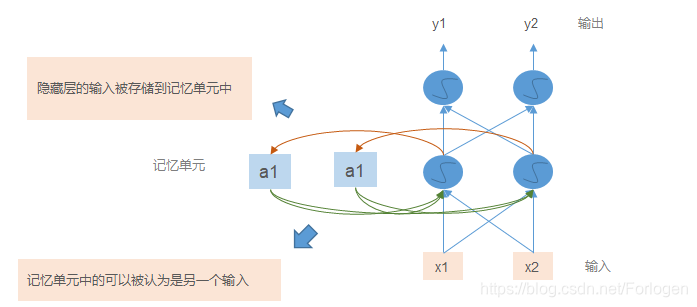
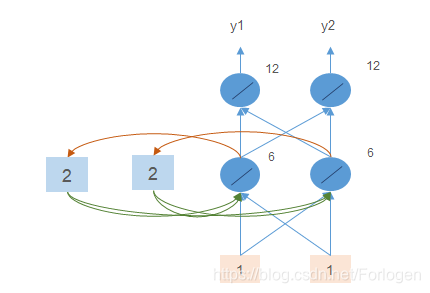
在这里插入图片描述

下面再通过一个简单的小栗子看一下上面所说的是什么意思，假设网络只有简单的三层，而且激活函数都是线性的，记忆单元中存储的值初始化为0，节点的输出自然也都是0，如下所示


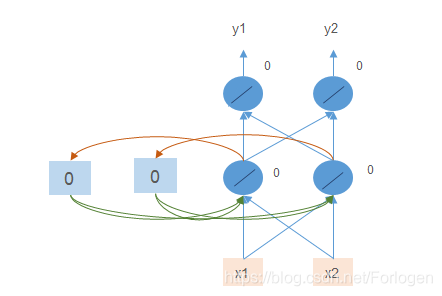
在这里插入图片描述

那么输入 [ 1 , 1 ] [1,1] [1,1]，各节点的输出如下所示，输出的结果为 [ 4 , 4 ] [4,4] [4,4]


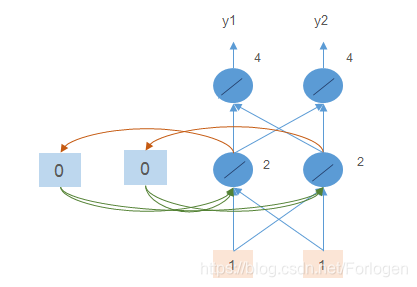
在这里插入图片描述

那么再输入 [ 1 , 1 ] [1,1] [1,1]，此时由于前面的输入，记忆单元中的值更新为2、2，所以隐藏层节点的输出就变成了 1 + 1 + 2 + 2 = 6 1+1+2+2=6 1+1+2+2=6，最后输出 [ 12 , 12 ] [12,12] [12,12]


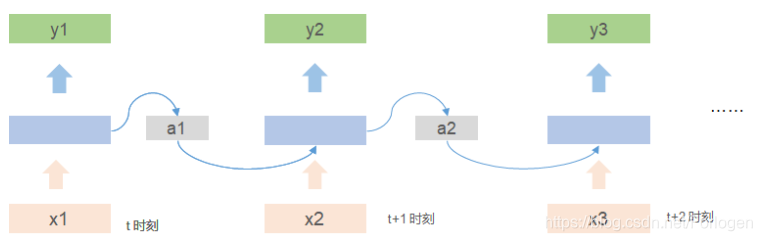
在这里插入图片描述

将多个简单的循环神经网络组合到一起，按照时间展开，就得到了一个简单的单向循环神经网络


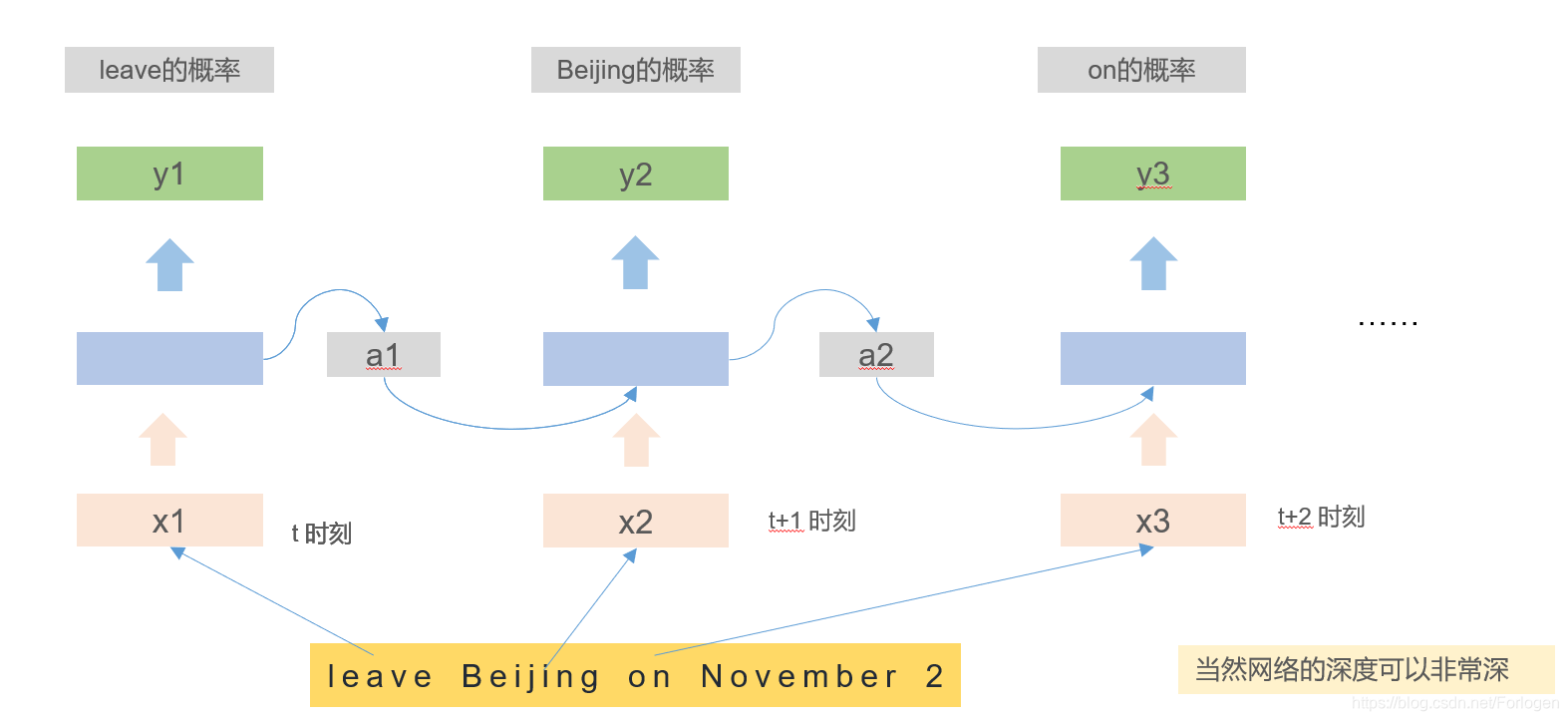
在这里插入图片描述

如果将"leave Beijing on November 2"输入到网络中，我们就可得到在Slot Filling问题中每个单词输入每个slot的概率值


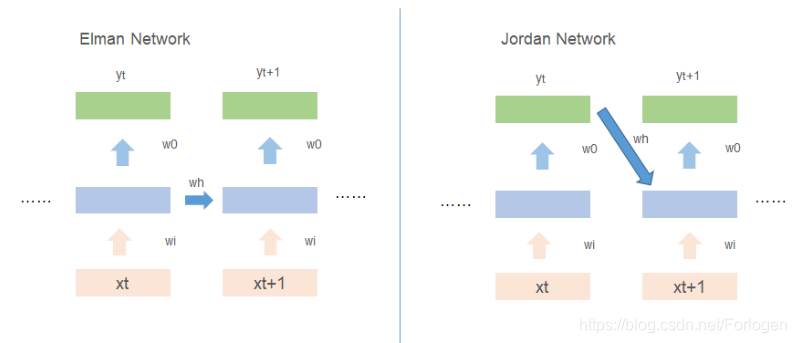
在这里插入图片描述

在单向的循环神经网络中，常用的有Elman Network、Jordan Network两种，不同之处在于对于记忆单元的更新，如下所示


在这里插入图片描述

在处理同一序列数据时，如果从前到后和从后到前同时进行，就得到了双向循环神经网络


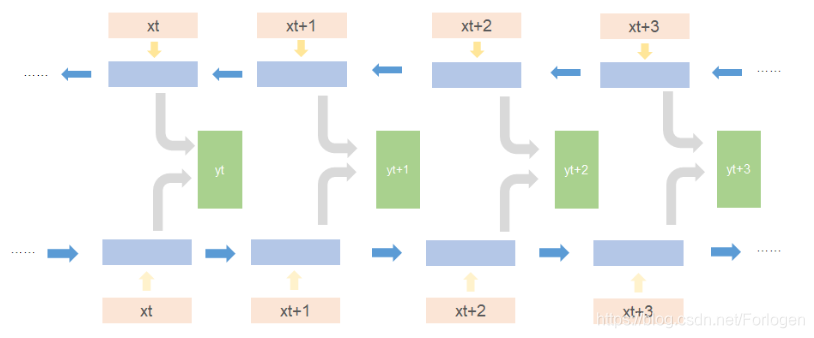
在这里插入图片描述

理论上，使用上面所提到的循环神经网络就可以建立长距离的依赖关系，但是有一个问题在于，当循环神经网络在时间维度上非常深时，就会出现梯度消失、梯度爆炸的问题。针对于梯度爆炸的问题，我们可以使用权重衰减、梯度截断等方法进行缓解，针对于梯度消失的问题，我们就可以使用LSTM。

长短期记忆（Long Short-Term Memory，LSTM）网络[Gers et al., 2000,Hochreiter and Schmidhuber, 1997] 是循环神经网络的一个变体，可以有效地解决简单循环神经网络的梯度爆炸或消失问题。LSTM中引入了门机制来控制信息传递的路径，引入了输入门（input gate）、输出门（output gate）和遗忘门（forget gate）三个门。


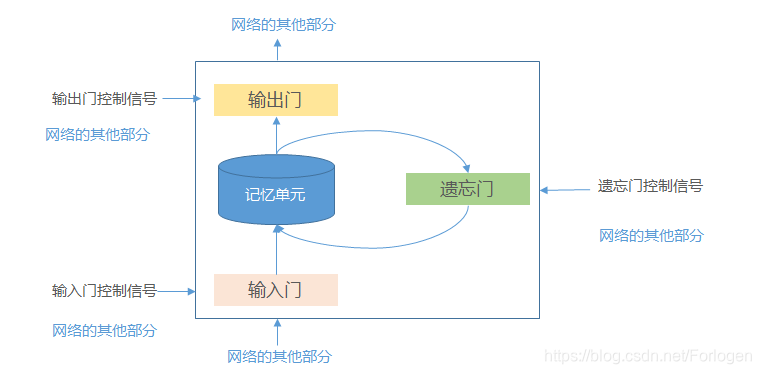
在这里插入图片描述

在基本的逻辑电路中，逻辑门只有两个取值 0 0 0和 1 1 1：0表示关闭，任何信息都不能通过；1表示开放，允许所有的信息通过。LSTM中的门类似于逻辑门，但它的取值在（0，1）之间，表示以一定的比例允许信息的通过。三个门的作用为：

  • 输入门：控制当前时刻的候选状态有多少信息需要保存
  • 输出门：控制当前时刻的内部状态有多少信息需要输出给外部状态
  • 遗忘门：控制上一时刻的内部状态需要遗忘多少信息

LSTM的简单结构如下所示


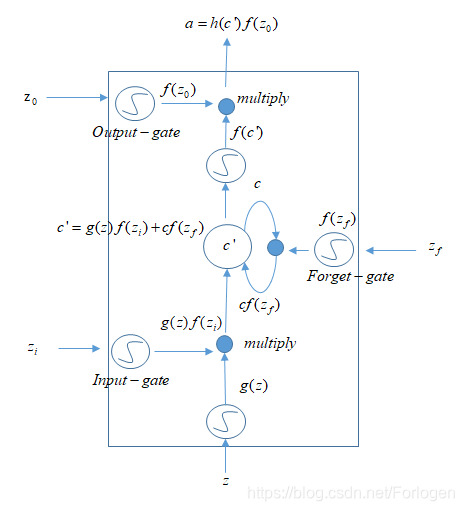
在这里插入图片描述

其中激活函数常使用的是Sigmoid函数，因为它可以将值挤压到（0，1）之间，与门机制的设定是一致的；而且由网络自己来控制门的开和闭。猛的一看，怎么这么复杂？！？下面我们就拿李宏毅老师所讲的“人肉LSTM”的例子来看一下它是怎么运行的。

假设 [ x 1 , x 2 , x 3 ] 、 y 、 M e m o r y   c e l l [x_{1},x_{2},x_{3}]、y、Memory\ cell [x1​,x2​,x3​]、y、Memory cell如下所示，规定：当 x 2 = 1 x_{2}=1 x2​=1时，将 x 1 x_{1} x1​中的值添加到记忆单元中；当 x 2 = − 1 x_{2}=-1 x2​=−1时，重置记忆单元；当 x 3 = 1 x_{3}=1 x3​=1时，输出记忆单元中的值


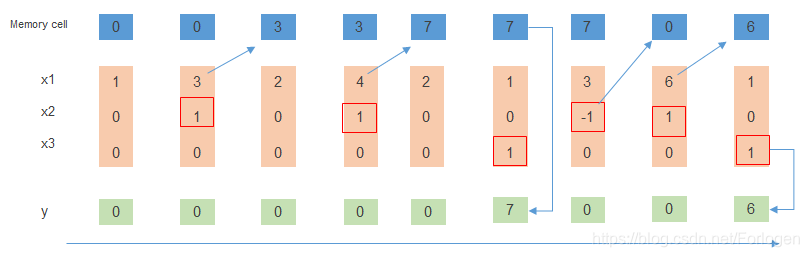
在这里插入图片描述

  • [ 1 , 0 , 0 ] [1,0,0] [1,0,0]： x 2 = 0 , x 3 = 0 x_{2}=0,x_{3}=0 x2​=0,x3​=0，输出和记忆单元中的值都是0
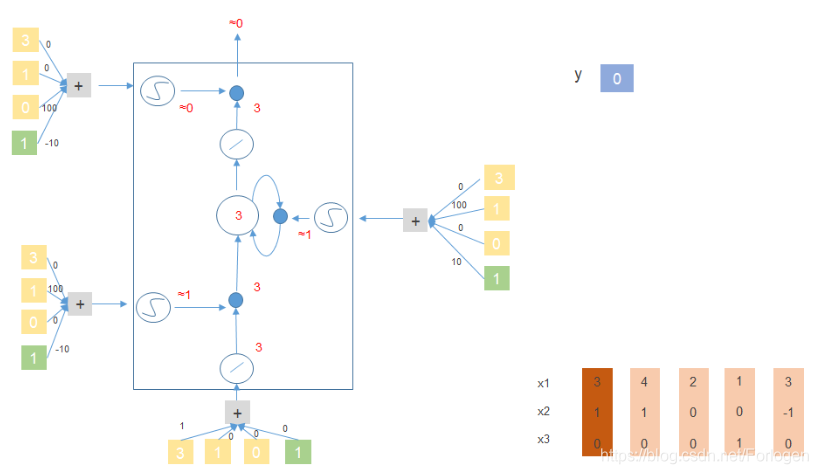
  • [ 3 , 1 , 0 ] [3,1,0] [3,1,0]： x 2 = 1 , x 3 = 0 x_{2}=1,x_{3}=0 x2​=1,x3​=0，需要将 x 1 x_{1} x1​的值添加到记忆单元中，在下一时刻，记忆单元中的值就变成了3
  • [ 2 , 0 , 0 ] [2,0,0] [2,0,0]： x 2 = 0 , x 3 = 0 x_{2}=0,x_{3}=0 x2​=0,x3​=0，输出和记忆单元中的值不做改变
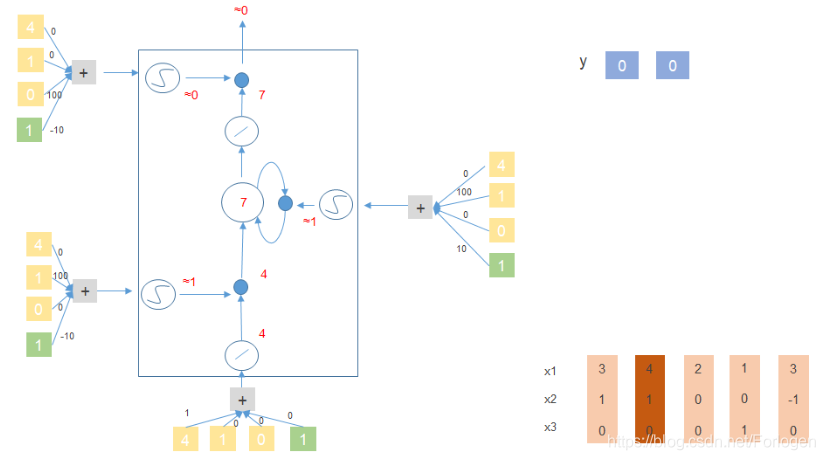
  • [ 4 , 1 , 0 ] [4,1,0] [4,1,0]： x 2 = 1 x_{2}=1 x2​=1， 需要将 x 1 x_{1} x1​中的值4添加到记忆单元中，在下一时刻，记忆单元中的值更新为 4 + 3 = 7 4+3=7 4+3=7
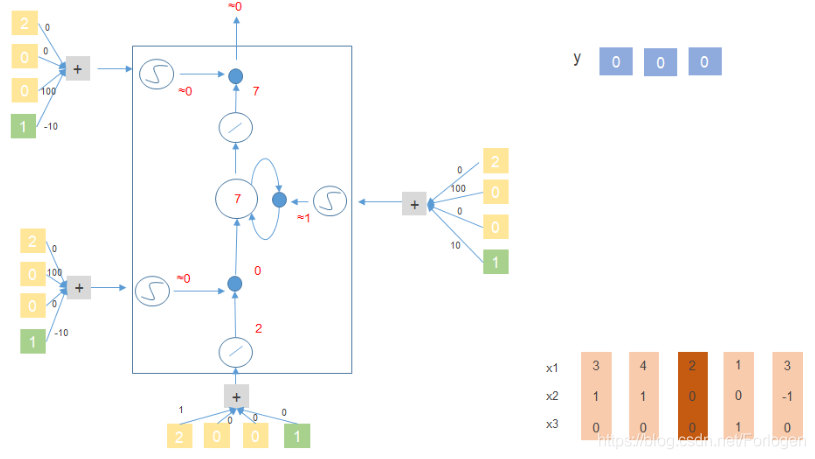
  • [ 2 , 0 , 0 ] [2,0, 0 ] [2,0,0]： x 2 = 0 , x 3 = 0 x_{2}=0,x_{3}=0 x2​=0,x3​=0，输出和记忆单元中的值不做改变
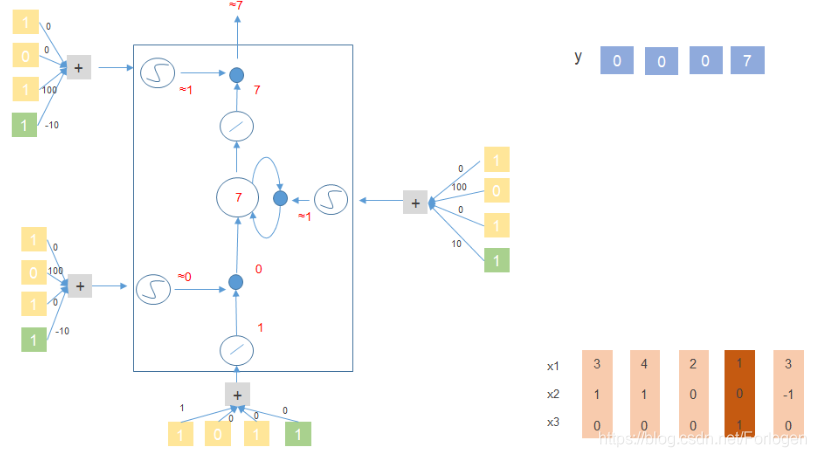
  • [ 1 , 0 , 1 ] [1,0,1] [1,0,1]： x 3 = 1 x_{3}=1 x3​=1 ，输出记忆单元中的值7
  • ……

下面以 [ 3 , 1 , 0 ] 、 [ 4 , 1 , 0 ] 、 [ 2 , 0 , 0 ] 、 [ 1 , 0 , 1 ] 、 [ 3 , − 1 , 0 ] [3,1,0]、[4,1,0]、[2,0,0]、[1,0,1]、[3,-1,0] [3,1,0]、[4,1,0]、[2,0,0]、[1,0,1]、[3,−1,0]来看一下它在上面提到的简单的LSTM结构中是怎么做的？


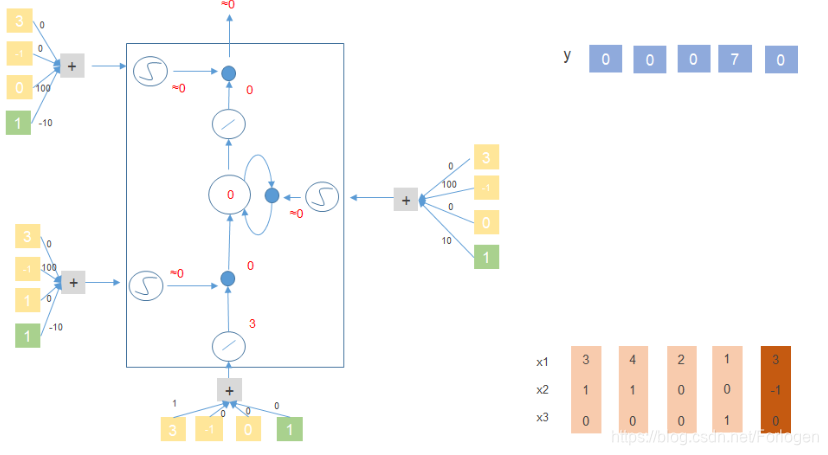
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

关于这个例子的PPT我重新做了一份，方便逐步理解，需要的可以到 https://download.youkuaiyun.com/download/forlogen/11160568 下载（P.S. 系统自动设置了下载要5个积分…如果有人知道怎么设置为不需积分，望告知一下）

相比于传统的前馈神经网络，每一个输入都需要作为LSTM所需的4个输入项，所以参数量就增加为之前的4倍


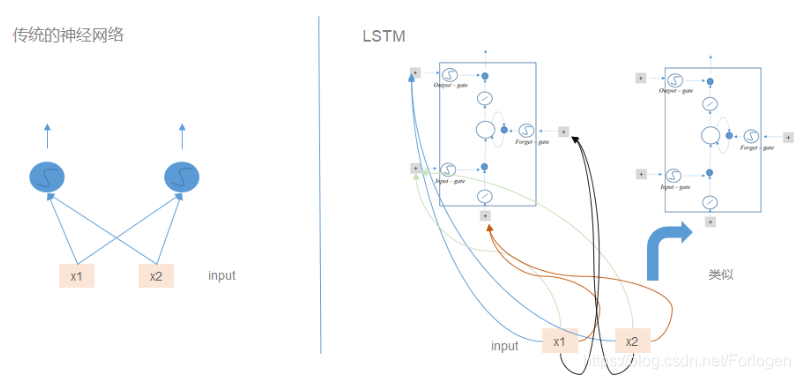
在这里插入图片描述

但是对于输入 x 1 x_{1} x1​（对于其他的输入同理，这里以 x 1 x_{1} x1​为例说明）来说，它并不直接作为LSTM的输入，而是先经过转换操作，得到四个向量 z f 、 z i 、 z 、 z o z_{f}、z_{i}、z、z_{o} zf​、zi​、z、zo​，它们的维度正好了记忆单元的个数相同，然后再分别作为不同时刻的对应输入，如下所示


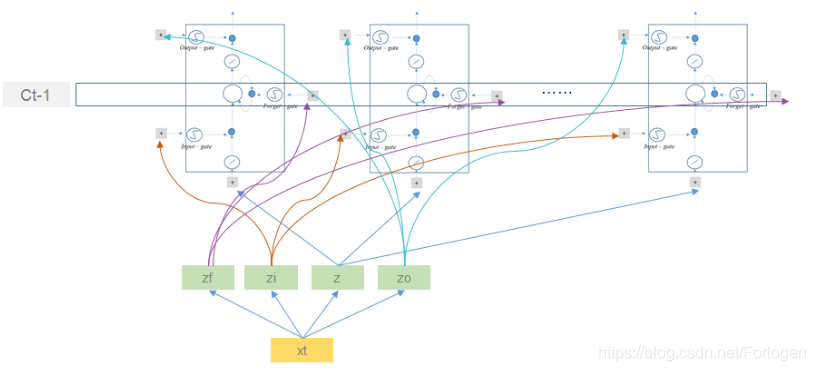
在这里插入图片描述

在每一个结构中的运算过程如下所示


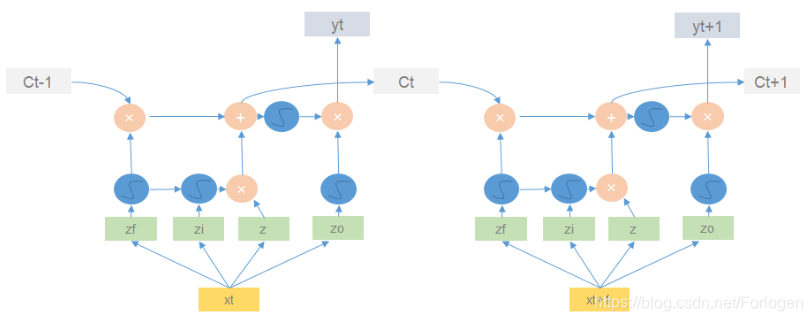
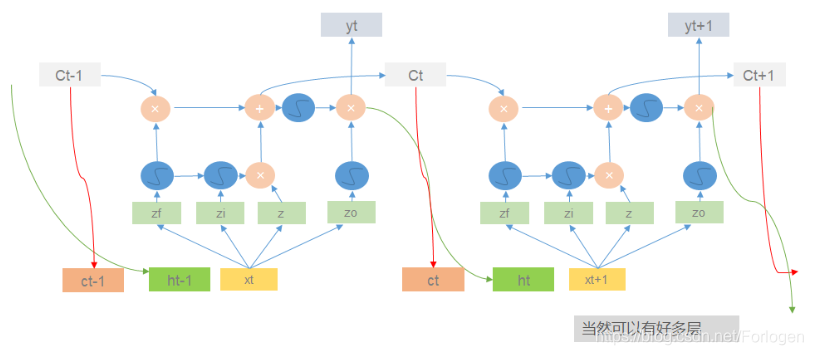
在这里插入图片描述

其实输入还不光有 x t x_{t} xt​，还有上一时刻的记忆单元中的值 c t − 1 c_{t-1} ct−1​、上一时刻输出值 h t h_{t} ht​,完整的LSTM结构如下所示


在这里插入图片描述

应用场景

  • 语音识别：输入的语音数据，生成相应的语音文本信息
  • 机器翻译：不同语言之间的相互转换
  • 音乐生成：使用RNN网络生成音乐，一般会用到RNN中的LSTM算法
  • 文本生成：利用RNN亦可以生成某种风格的文字
  • 情感分类：输入文本或者语音的评论数据，输出相应的打分数据
  • DNA序列分析：输入的DNA序列，输出蛋白质表达的子序列
  • 视频行为识别：识别输入的视频帧序列中的人物行为
  • 实体名字识别：从文本中识别实体的名字
  • ……

其他

零基础入门深度学习(5) - 循环神经网络

零基础入门深度学习(6) - 长短时记忆网络(LSTM)

Understanding LSTM Networks

李宏毅老师《机器学习》

图解LSTM与GRU单元的各个公式和区别

Deep Learning Basics: Gated recurrent unit (GRU)

Understanding GRU Networks

循环神经网络
Line2333的博客
04-14 454
特点：上一阶段（时间步）的输出作为输入进入当前时间步。 预测模型 循环神经网络由循环神经原组成，循环神经元一般有两个输入，一个是前阶段的信息，一个是当前阶段的信息。同时产生一个输出，可以作为下一阶段的输入。 循环神经网络采用多种模型。 左上：每个时间步有一个输入，同时产生一个输出 右上：一串输入，最后产生一个输出。 左下：一个输入，一串输出 右下：编码-解码器。 每一层的...
九、【人工智能】【机器学习】【监督学习】-循环神经网络 (RNN)
技术分享、程序员趣事、行业趋势等内容！
07-11 1036
在先前的文章系列中，我们深入探讨了机器学习的基础框架和算法分类，为读者构建了关于这一领域的坚实理论基础。本章节我们将焦点转向监督学习领域中的一个核心算法—— 卷积神经网络 (CNN)，旨在详尽解析其内在逻辑、应用实践及重要参数调整策略。监督学习（Supervised Learning）是机器学习中的一种主要方法，其核心思想是通过已知的输入-输出对（即带有标签的数据集）来训练模型，从而使模型能够泛化到未见的新数据上，做出正确的预测或分类。
RNN
热门推荐
对算法理论、算法工程落地、大数据工具等感兴趣
06-06 32万+
RNN（Recurrent Neural Network）是一类用于处理序列数据的神经网络。首先我们要明确什么是序列数据，摘取百度百科词条：时间序列数据是指在不同时间点上收集到的数据，这类数据反映了某一事物、现象等随时间的变化状态或程度。这是时间序列数据的定义，当然这里也可以不是时间，比如文字序列，但总归序列数据有一个特点——后面的数据跟前面的数据有关系。 ...
深度学习5——循环神经网络
最新发布
DUTBenjamin的博客
06-12 1054
循环神经网络（RNN）是一类专门处理序列数据的神经网络，具有记忆能力，能够利用历史信息影响当前输出。其核心结构包括隐藏状态的循环连接，通过参数共享机制处理变长序列。RNN与单向流动的前馈神经网络形成鲜明对比，在语音识别、机器翻译等任务中表现优异。为了解决长程依赖问题，LSTM和GRU引入门控机制，分别通过记忆细胞和三门控（遗忘门、输入门、输出门）或双门控（更新门、重置门）选择性保留信息。此外，双向RNN（Bi-RNN）结合前后文信息，而深层RNN通过多层堆叠增强特征提取能力。训练方法上，RNN采用随时间反向
智创 AI 新视界 -- 改进 AI 循环神经网络（RNN）的实践探索（16 - 12）
【青云交】华为云云享专家，在技术圈个人影响力位居前17，跻身博客之星 TOP23。同时荣登【原力榜、作者周榜、领军人物和综合热榜】四榜榜首，破优快云排行榜记录！苏州地区各榜也统统拿下榜首之位，实力爆棚！非常感谢全网十多万粉丝的喜欢和关注！
12-12 2132
本文围绕 RNN 的改进展开深度实践探索，从基础原理回顾与局限性剖析入手，通过实际案例和实验数据展现问题所在；接着详细阐述门控机制（LSTM 和 GRU）的优化应用及在股票预测、诗歌生成等任务的出色表现，以及注意力机制与 RNN 及其变体的融合创新，如在机器翻译、图像描述生成任务中的显著提升效果，给出丰富详细且优化后的代码示例，最后提出互动问题并自然引出下一篇关于 AI 伦理困境的文章。
神经网络和深度学习（一）——初识神经网络
CUG_UESTC的博客
08-15 8万+
神经网络和深度学习 神经网络：一种可以通过观测数据使计算机学习的仿生语言范例 深度学习：一组强大的神经网络学习技术神经网络和深度学习目前提供了针对图像识别，语音识别和自然语言处理领域诸多问题的最佳解决方案。传统的编程方法中，我们告诉计算机如何去做，将大问题划分为许多小问题，精确地定义了计算机很容易执行的任务。而神经网络不需要我们告诉计算机如何处理问题，而是通过从观测数据中学习，计算出他自己的解决方案
机器学习基础（四）—初识神经网络
weixin_44027006的博客
03-20 447
1 多变量Logistic回归： 多变量Logistic回归的基本思想就是：假设又K个类别，那么就用K个分类器，一个一个的挑出每一个类别与其他的类别进行比较。比如：类别包括：晴，阴天，雨三个分类。那么我就需要三个分类器。第一个分类器将晴作为一类，其他的作为一类利用二元Logistic回归的思想找到最优θ，依此类推。 首先获取数据，查看数据 import numpy as np import p...
AI开发：卷积神经网络CNN原理初识，简易例程 - 机器学习
minstbe的博客
12-08 1319
今天说的CNN，并不是我们熟知的美国有线电视新闻网。那什么是CNN呢？ Convolutional Neural Networks, CNN）简单来说，就是用一个筛子来筛面粉的。筛子就是卷积核，面粉就是被筛的信息，晒出来的面粉就是新生成或者说被抽离的特征。有很多把筛子组成的网络一起来筛信息，就组成了一个卷积神经网络。卷积神经网络（CNN）是一种模仿人类视觉系统的算法，常用于图像和视频处理。它的基本思想是通过多个“卷积层”逐步提取图像的特征。例如，在处理一张照片时，网络首先识别图像的基本边缘或颜色，再逐渐发现
rnn_demo:PyBrain 的循环神经网络演示
06-27
循环神经网络演示 目的 预测 10x10 区域内弹跳球的路径。 模型 Elman/Jordan Network（以下是Jordan 模型）。 输入：x,y 位置和速度。 训练数据 从data/ball_data.py生成弹跳球数据。 怎么跑 安装并激活虚拟环境后，在下面运行。 python rnn_demo.py （默认是 Jordan，如果你想跑 Elman，加E选项）。 依赖关系如下。 麻木的 scipy matplotlib
评论 1
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值