首先给出有关GAN的相关东西:
paper:NIPS 2016 Tutorial: Generative Adversarial Networks
Author: Ian Goodfellow
Paper Download: https://arxiv.org/abs/1701.00160
Video: https://channel9.msdn.com/Events/Neural-Information-Processing-Systems-Conference/Neural-Information-Processing-Systems-Conference-NIPS-2016/Generative-Adversarial-Networks
前述
生成模型在机器学习甚至深度学习中都是一个主要的内容,比如我们的数据是大量的唐诗的文本,经过学习我们希望得到一个很好的生成模型,可以自己写一些诗;或者我们的数据是关于二次元人物头像,希望学习得到的生成模型可以自己画出一些类似的图像。
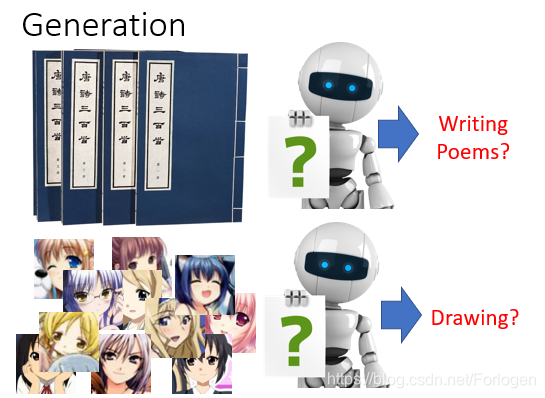
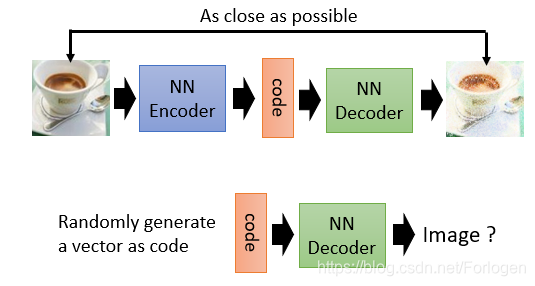
关于这方面的模型有很多,比如Auto-encoder:在训练阶段,将图像数据输入到一个NN(neural network) Encoder中,得到code,然后再将其输入到NN Decoder中就可以生成一个新的图像,我们希望经过不断地训练,由Auto-encoder生成的图像尽可能的接近真实数据。训练结束后,输入一些随机产生的code 的向量到NN Decoder中,就可以产生一些图像数据。
比如在MNIST上进行实验,将手写图像的输入到NNEncoder中就可以得到一个2D的code,然后将其输入到NN Decoder中就可以得到和真实数据很近似的新图像数据。比如将 [ − 1.5 , 0 ] [-1.5,0] [−1.5,0]传入NN Decoder中得到手写数字0的图像,将 [ 1.5 , 0 ] [1.5,0] [1.5,0]传入NN Decoder中得到手写数字1的图像
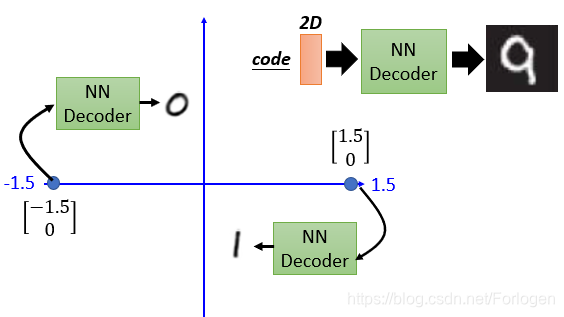
经过多次实验就可以得到如下的结果图,当我们输入不同的2D向量时,就可以得到不同的关于手写数字的新图像

另一种方式是VAE,基本的流程如下,它和Auto-Encoder一样都有一个NN Ecoder和一个NN Dcoder,不同的是输入到NN Decode中的内容。将数据输入到NN Ecoder中会产生code { m 1 , m 2 , m 3 } \{m_{1},m_{2},m_{3}\} {m1,m2,m3}和 { σ 1 , σ 2 , σ 3 , } \{\sigma_{1},\sigma_{2},\sigma_{3},\} {σ1,σ2,σ3,},然后再随机的生成噪声数据 { e 1 , e 2 , e 3 } \{e_{1},e_{2},e_{3}\} {e1,e2,e3},然后做如图所示的运算生成 { c 1 , c 2 , c 3 } \{c_{1},c_{2},c_{3}\} {c1,c2,c3},输入到NN Decoder中便得到一个输出。这里同样是希望output和input越接近越好,所以去最小化两者之间的误差。但是这样做会使得 { σ 1 , σ 2 , σ 3 } \{\sigma_{1},\sigma_{2},\sigma_{3}\} {σ1,σ2,σ3}的值都为0,所以需要对 σ i , i = 1 , 2 , 3 \sigma_{i},i=1,2,3 σi,i=1,2,3,做如下的限制 ∑ i = 1 3 ( e x p ( σ i ) − ( 1 + σ i ) + ( m i ) 2 ) \sum_{i=1}^3(exp(\sigma_{i})-(1+\sigma_{i})+(m_{i})^2) ∑i=13(exp(σi)−(1+σi)+(mi)2)
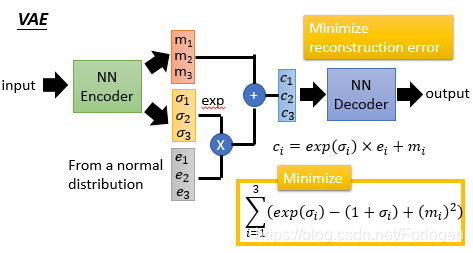
但是VAE存在一个问题那就是,经过NN Decoder生成的图像,可能不同的数据之间仅有一个像素不同,对于它来说都认为是一样接近真实的数据。但是不同的输出图像对于人来说,效果是不一样的,也可以说它无法真正的生成对真实图像的模拟。
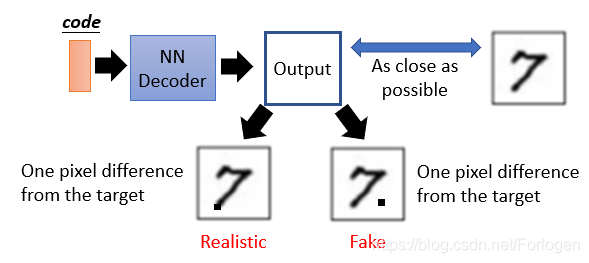
P.S. 对于Auto-encoder和VAE之前并没有学习过,有兴趣的同学可以补一下课~~
下面开始学习GAN的相关内容,为了方便表述,生成器Generator一律用G表示,判别器Discriminator一律用D表示。在GAN中,G类似于VAE中的Decoder,随机的生成一些噪声样本输入到G中生成一些图像,标记为0,真实的图像标记为1,一起作为输入传到D中,D会判断出哪些是真实的,哪些是G生成的。
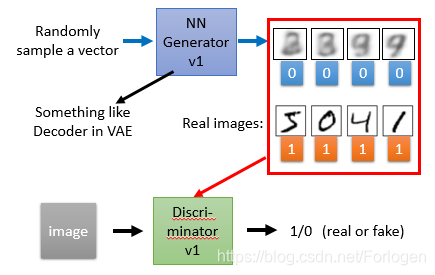
通常G和D都是神经网络,当D固定时,使用梯度下降法更新G的参数,通过不断的迭代,两者相互对抗,使得G生成的图像越来越接近真实图像,D无法判别输入的图像是真是假。

GAN
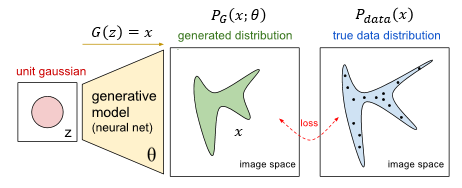
下面我们从公式推导的过程来看一下GAN的原理,用 p d a t a ( x ) p_{data}(x) pdata(x)来表是真实数据的分布,使用 p G ( x ; θ ) p_{G}(x;\theta) pG(x;θ)来表示随机噪声数据的分布,它受参数 θ \theta θ( θ \theta θ这里是一组参数,而不只是一个)限制。这里 p G ( x ; θ ) p_{G}(x;\theta) pG(x;θ)可以是任何的分布类型,对应的 θ \theta θ就表示不同的含义,比如当 p G ( x ; θ ) p_{G}(x;\theta) pG(x;θ)表示高斯分布时, θ \theta θ就表示高斯分布的均值和方差,如下图所示,均值就是黄色点,方便就表示蓝色圆圈的范围。我们希望 p G ( x ; θ ) p_{G}(x;\theta) pG(x;θ)尽可能的接近 p d a t a ( x ) p_{data}(x) pdata(x),这样生成的图像就越接近真实图像。
为了计算 p G ( x ; θ ) p_{G}(x;\theta) pG(x;θ)中的 θ \theta θ,我们从 p d a t a ( x ) p_{data}(x) pdata(x)中随机抽样 { x 1 , x 2 , … , x m } \{x^1,x^2,…,x^m\} {x1,x2,…,xm},然后建立似然函数L,通过最大化似然函数来求得最佳的 θ \theta θ,这里用 θ ∗ \theta^{*} θ∗表示。

使用极大似然函数求解 θ ∗ \theta^{*} θ∗的过程如下所示,最好的结果可以看作是通过最小化KL散度(用来衡量两个分布的相似性)来求得解。那么这里就有一个问题,如果像其他算法一样假设噪声数据是一个高斯分布,在这里最后的效果往往很差,那么我们如何得到一个通用性高的 p G ( x ; θ ) p_{G}(x;\theta) pG(x;θ),同时又有很好的效果呢?

在GAN中G通常都是一个神经网络模型,它接收一个可能是任何分布的随机噪声数据
z
z
z,输入一个
g
e
n
e
r
a
t
e
d
d
i
s
t
r
i
b
u
t
i
o
n
generated \ distribution
generated distribution,它和之前的分布就会有很大的差别,建立损失函数表示它和真是数据分布的差距,通过最小化损失函数,得到一个不错的G。具体的过程我们可以用下面这个公式表达
p
G
(
x
)
=
∫
z
p
p
r
i
o
r
(
z
)
I
[
G
(
z
)
=
x
]
d
z
p_{G}(x)=\int_{z}p_{prior}(z)I_{[G(z)=x]}dz
pG(x)=∫zpprior(z)I[G(z)=x]dz
其中,因为假设此时分布的选定的,所以
p
G
(
X
)
p_{G}(X)
pG(X)中没有参数
θ
\theta
θ;
p
p
r
i
o
r
(
z
)
p_{prior}(z)
pprior(z)表示不同的
z
z
z出现的概率;
G
(
z
)
G(z)
G(z)表示输入到G中的
z
z
z生成的数据;函数
I
[
G
(
z
)
=
x
]
I_{[G(z)=x]}
I[G(z)=x]表示G生成的数据和真实数据x的差异,如果认为是相同的,则值为1,否则值为0。然后通过积分所有的
z
z
z来建立如上所示的似然函数
L
=
∏
i
=
1
m
p
G
(
x
i
;
θ
)
L=\prod_{i=1}^m p_{G}(x^i;\theta)
L=i=1∏mpG(xi;θ)但是它是难以计算的。
而Ian Goodfellow天才般的提出的GAN就解决了这个问题。在GAN中,G是一个函数(function),输入 z z z输出 x x x,具体来说给G一个 p p r i o r ( z ) p_{prior}(z) pprior(z),最后给出一个可能的分布 p G ( x ) p_{G}(x) pG(x)。D也可以看做是一个函数,接收 x x x输出一个标量,表示判别的结果。建立函数 V ( G , D ) V(G,D) V(G,D)来衡量 p G ( x ) p_{G}(x) pG(x)和 p d a t a ( x ) p_{data}(x) pdata(x)的不同,通过 a r g min G max D V ( G , D ) arg\min \limits_{G}\max \limits_{D}V(G,D) argGminDmaxV(G,D)来得到最优解 G ∗ G^{*} G∗。

根据GAN的G和D相互对抗的思想,我们可以将函数
V
(
G
,
D
)
V(G,D)
V(G,D)写成如下的形式
V
=
E
x
∼
p
d
a
t
a
[
l
o
g
D
(
x
)
]
+
E
x
∼
p
G
[
l
o
g
(
1
−
D
(
x
)
)
]
V=E_{x\sim p_{data}}[logD(x)]+E_{x\sim p_{G}}[log(1-D(x))]
V=Ex∼pdata[logD(x)]+Ex∼pG[log(1−D(x))]
给定一个G,通过
max
D
V
(
G
,
D
)
\max \limits_{D}V(G,D)
DmaxV(G,D)来提高D的判别能力,尽可能的找出
p
G
p_{G}
pG和
p
d
a
t
a
p_{data}
pdata的不同。如果D给定时,同样要找到一个G,来使得
p
G
p_{G}
pG尽可能的和
p
d
a
t
a
p_{data}
pdata相似。
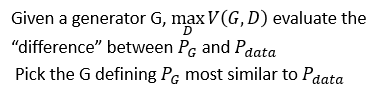
接下来我们通过图像来形象的理解一下 G ∗ = a r g min G max D V ( G , D ) G^{*}=arg\min \limits_{G}\max \limits_{D}V(G,D) G∗=argGminDmaxV(G,D),如下所示,横轴表示D的范围,纵轴表示 V ( G i , D ) V(G_{i},D) V(Gi,D)的值,如果G给定时,不同的D则 V ( G i , D ) V(G_{i},D) V(Gi,D)就会有不同的结果,那么对于图中所示的三个G,它的最大值就出现在红点的位置。
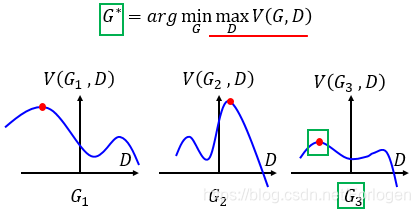
将前面关于V的表达式进行如下的转换
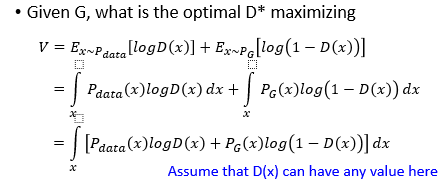
为了得到 D ∗ D^{*} D∗,就要最大化它,等价的就是要最大化积分号中的部分 p d a t a ( x ) l o g D ( x ) + p G ( x ) l o g ( 1 − D ( x ) ) p_{data}(x)logD(x)+p_{G}(x)log(1-D(x)) pdata(x)logD(x)+pG(x)log(1−D(x))做以下的表示规定:
- a a a: p d a t a ( x ) p_{data}(x) pdata(x)
- b b b: p G ( x ) p_{G}(x) pG(x)
-
D
D
D:
D
(
x
)
D(x)
D(x)
则可以将其变成 f ( D ) = a l o g ( D ) + b l o g ( 1 − D ) f(D)=alog(D)+blog(1-D) f(D)=alog(D)+blog(1−D),求 f ( D ) f(D) f(D)的最大值是很简单的。最后求得 D ∗ ( x ) = p d a t a ( x ) p d a t a ( x ) + p G ( x ) D^{*}(x)=\frac {p_{data}(x)}{p_{data}(x)+p_{G}(x)} D∗(x)=pdata(x)+pG(x)pdata(x)它的取值范围是 [ 0 , 1 ] [0,1] [0,1]

那么对于不同的G就会有不同的 D ∗ ( x ) D^{*}(x) D∗(x),表现在图上就是会有不同的最大值点,而它与横轴之间的距离(图中绿色虚线部分)就表示了 p G i p_{G_{i}} pGi和 p d a t a p_{data} pdata的差距
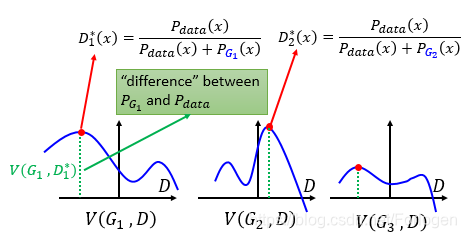
将 D ∗ ( x ) D^{*}(x) D∗(x)带入 V V V的表达式有如下的样子,然后在 l o g log log的表达式上下同除以2,就可以得到如下的表达式
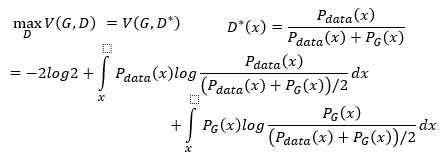
而第一个积分号的内容表示了 p d a t a ( x ) p_{data}(x) pdata(x)和 ( p d a t a ( x ) + p G ( x ) ) / 2 (p_{data}(x)+p_{G}(x))/2 (pdata(x)+pG(x))/2的KL散度,同样的第二个积分里的内容表示了 p G ( x ) p_{G}(x) pG(x)和 ( p d a t a ( x ) + p G ( x ) ) / 2 (p_{data}(x)+p_{G}(x))/2 (pdata(x)+pG(x))/2的KL散度,所以我们可以写成如下的形式 − 2 l o g 2 + K L ( p d a t a ( x ) ∣ ∣ p d a t a ( x ) + p G ( x ) 2 ) + K L ( p G ( x ) ∣ ∣ p d a t a ( x ) + p G ( x ) 2 ) -2log2+KL(p_{data}(x)|| \frac{p_{data}(x)+p_{G}(x)}{2})+KL(p_{G}(x)|| \frac{p_{data}(x)+p_{G}(x)}{2}) −2log2+KL(pdata(x)∣∣2pdata(x)+pG(x))+KL(pG(x)∣∣2pdata(x)+pG(x))
而这样的形式类似于
J
S
D
(
P
∣
∣
Q
)
=
1
2
D
(
p
∣
M
∣
)
+
1
2
D
(
Q
∣
∣
M
)
,
M
=
1
2
(
P
+
Q
)
JSD(P||Q)=\frac{1}{2}D(p|M|)+\frac{1}{2}D(Q||M),M=\frac{1}{2}(P+Q)
JSD(P∣∣Q)=21D(p∣M∣)+21D(Q∣∣M),M=21(P+Q)
所以可以将其写成Jensen-Shannon散度的形式
−
2
l
o
g
2
+
2
J
S
D
(
p
d
a
t
a
(
x
)
∣
∣
P
G
(
x
)
)
-2log2+2JSD(p_{data}(x)||P_{G}(x))
−2log2+2JSD(pdata(x)∣∣PG(x))
下面对GAN做一个小总结,那么最后得到的最优的G,自然就是使得 p G ( x ) = p d a t a ( x ) p_{G}(x)=p_{data}(x) pG(x)=pdata(x)

通过上面的分析,知道了如何设函数来得到最优的G和D,以及最优的结果应该是什么。那么如何来不断更新G和D,来得到最优的 G ∗ G^{*} G∗和 D ∗ D^{*} D∗呢?
假设此时D是固定的,将 max D V ( G , D ) \max \limits_{D}V(G,D) DmaxV(G,D)记为 L ( G ) L(G) L(G),为了得到最好的G,就要最小化这个损失函数,这里使用梯度下降法更新参数 θ G \theta_{G} θG
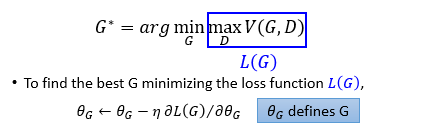
假设这里的D不是无限个,只有三个,那么用 f ( x ) f(x) f(x)表示 f ( x ) = m a x { D 1 ( x ) , D 2 ( x ) , D 3 ( x ) } f(x)=max\{D_{1}(x),D_{2}(x),D_{3}(x)\} f(x)=max{D1(x),D2(x),D3(x)},它们表现在图中如下所示,当然可能不一定是直线,这里为了方便表述,假设它们都是直线。那么我们如何来求 f ( x ) f(x) f(x)对 x x x的微分呢?首先要看 x x x落在那个区域中,区域中哪个 D i ( x ) D_{i}(x) Di(x)最大, f f f就等于哪个 D i ( x ) D_{i}(x) Di(x),然后进行微分。因为这里是要最小化损失函数,如果开始落在 D 1 ( x ) D_{1}(x) D1(x)的区域中,微分后就会告诉你应该往右走,当落到 D 2 ( x ) D_{2}(x) D2(x)的区域中,微分后就会告诉你应该继续往右走,就是这样一个过程。
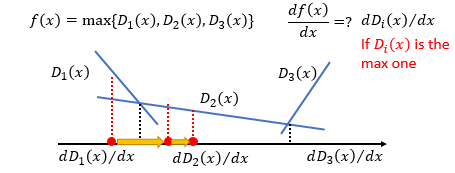
所以我们可以使用如下的方法来找到一个G来最小化 max D V ( G , D ) \max \limits_{D}V(G,D) DmaxV(G,D)。初始时给定一个 G 0 G_{0} G0,然后找一个 D 0 ∗ D^{*}_{0} D0∗来最大化 V ( G , D ) V(G,D) V(G,D),然后利用梯度下降来更新参数 θ G \theta_{G} θG得到一个新的 G 1 G_{1} G1,接着使用相同的方法不断的更新下去,就会得到 G ∗ G^{*} G∗。

在更新过程中可能会有一个小问题,当 D 0 ∗ D^{*}_{0} D0∗固定时, G 1 G_{1} G1相比 G 0 G_{0} G0就会减小 p d a t a ( x ) p_{data}(x) pdata(x)和 p G ( x ) p_{G}(x) pG(x)之间的KL散度。但是如果下一个 D 1 ∗ D^{*}_{1} D1∗和 D 0 ∗ D^{*}_{0} D0∗很接近时,下个更新过程可能就会反而增大了 p d a t a ( x ) p_{data}(x) pdata(x)和 p G ( x ) p_{G}(x) pG(x)之间的KL散度。为了解决这个问题,参考其他算法使用梯度下降的过程,不要更新G太多次就可以了。
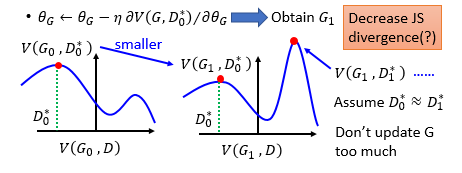
理论上这样是可行的,在实际操作中,我们往往进行如下的操作得到 V ~ \tilde{V} V~。这个形式和二分类算法中处理交叉熵的过程是不是很相似呢?

那么将从抽样得到的看做是positive examples,将从抽样得到的看做negative examples,前面最大化函数 V V V的过程就可以看成等价的最小化 L L L。

下面给出GAN算法的描述,,它主要是两个过程:学习G和学习D。为了取得比较稳定的效果,最好是训练k次D后训练1次G,在原始的论文中,作者是只训练1次D,就去训练G。

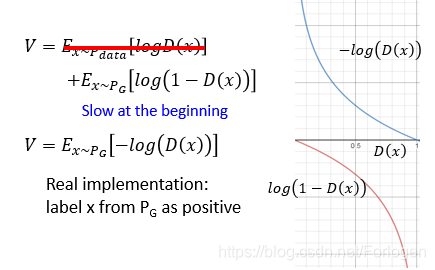
此外还需注意一个小问题,就是在实际情况中,常用
−
l
o
g
(
D
(
x
)
)
-log(D(x))
−log(D(x))代替
V
V
V中
E
x
∼
p
d
a
t
a
[
l
o
g
(
D
(
x
)
)
]
E_{x \sim p_{data}}[log(D(x))]
Ex∼pdata[log(D(x))]的
l
o
g
D
(
x
)
logD(x)
logD(x)
。因为这样可以使得G在一开始就有较大的梯度,训练过程中G在一开始生成的图像很轻易的就被D判别出来,影响最终的效果。







 本文详细介绍了生成对抗网络(GAN)的工作原理及其实现过程。通过对比Auto-encoder和VAE,阐述了GAN中生成器(G)与判别器(D)相互博弈的机制,并通过数学推导解释了GAN如何优化生成数据质量。
本文详细介绍了生成对抗网络(GAN)的工作原理及其实现过程。通过对比Auto-encoder和VAE,阐述了GAN中生成器(G)与判别器(D)相互博弈的机制,并通过数学推导解释了GAN如何优化生成数据质量。

















 525
525

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








