背景
在如今大数据的时代,我们可以获取到的数据量很大很大,但是更多情况下它们只是数据,存储在了某个地方。如何从中获取到一些有价值的东西,成为一个很迫切的需求。比如各大电商网站每天都会收集到很多用户大量的购物数据,如果从中能知道用户的购物习惯,就可以为他们推荐更合适的商品,从而提高收益;或是在线下的门店中,同样会收集到大量的购物信息,如果知道了大多数人购物的习惯(比如什么东西经常一起购买等),就可以将经常一起购买的东西放的近一些,从而提高不同种类商品的销售额。其中啤酒和尿布就是一个著名的例子。
Apriori算法简介
在处理上述的问题中,Apriori算法是数据挖掘中经典的挖掘频繁项和关联规则的算法。它是Agrawal和R.Srikant在1994年提出的,为布尔关联规则挖掘频繁项集合原创性算法。Apriori算法使用一种称为逐层搜索的迭代方法,其中k项集用于探索(k+1)项集。首先,通过扫描数据库,累计每个项的计数,并收集满足最小支持度的项,找出频繁1项集的集合。该集合记为L1。然后,使用L1找出频繁2项集的集合L2,使用L2找出L3,如此下去,直到不能再找到频繁k项集。每找出一个Lk需要一次数据库的完整扫描。
基本概念
在学习Apriori算法前先来了解一下涉及的基本概念
-
项与项集:例如itemset={item1, item_2, …, item_m},其中itemi(i=1,2,…,m)是项,itemset是项集,包含K个项的项集称为K项集
-
关联规则:形如 A ⇒ B A\Rightarrow B A⇒B的蕴含式,其中A、B都是项集的子集,A、B都不为空且交集为空
-
支持度: A ⇒ B A\Rightarrow B A⇒B在事务集D中成立,具有支持度s是指s在D中包含 A ∪ B A∪B A∪B的百分比,即 s u p p o r t ( A ⇒ B ) = s u p p o r t ( A B ) = P ( A B ) = n u m b e r ( A B ) n u m ( A l l S a m p l e s ) support(A\Rightarrow B)=support(AB) =P(AB) = \frac{number(AB)}{num(All Samples)} support(A⇒B)=support(AB)=P(AB)=num(AllSamples)number(AB)
-
置信度: A ⇒ B A\Rightarrow B A⇒B在事务集D中成立,具有置信度s是指s在D中包含A的事务同时也包含B的事务的百分比,即 c o n f i d e n c e ( A ⇒ B ) = P ( B ∣ A ) = s u p p o r t ( A B ) s u p p o r t ( A ) = s u p p o r t − c o u n t ( A B ) s u p p o r t − c o u n t ( A ) confidence(A\Rightarrow B) = P(B|A)= \frac{support(AB)}{support(A)} = \frac{support - count(AB)}{support-count(A)} confidence(A⇒B)=P(B∣A)=support(A)support(AB)=support−count(A)support−count(AB)
-
项集的出现频度:包含项集的事务数,简称为项集的频度、支持度计数或计数
-
频繁项集:如果项集I的相对支持度满足事先定义好的最小支持度阈值(即I的出现频度大于相应的最小出现频度(支持度计数)阈值),则I是频繁项集
-
强关联规则:满足最小支持度和最小置信度的关联规则,即待挖掘的关联规则
-
真超项集:如果Y是X的真超项集,则X中的每个项都在Y中,但是Y中至少有一个项不在X中
-
闭频繁项集:如果在D中X不存在真超项集Y使Y在D中具有相同的支持度计数,称X是闭频繁项集
-
极大频繁项集:如果X是频繁的,并且不存在超项集Y使得X包含于Y,以及Y在D中是频繁的,称X是极大频繁项集
-
关联规则的挖掘过程:
-
找出所有的频繁项集:项集中每一个频繁出现的次数 c o u n t ≥ m i n s u p count≥min_{sup} count≥minsup,它是整个过程最关键的一步
-
由频繁项集产生关联规则:找出满足最小支持度和最小置信度的规则
那么最小支持度和最小的置信度在实际中究竟有什么含义呢?其实它们表征了所挖掘出的规则在多大程度上有意义的。比如一个很常见的例子,购买啤酒的人也倾向于同时购买尿布,同时分析收集的数据我们可以得到如下的关联规则: 啤 酒 ⇒ 尿 布 啤酒\Rightarrow尿布 啤酒⇒尿布 (“60%”, 100%), 尿 布 ⇒ 啤 酒 尿布\Rightarrow啤酒 尿布⇒啤酒 (“60%”, 75%)。
那么我们如何向不懂得数据挖掘的人来解释这两条规则呢?它们的置信度都是60%,也就是有60%的人会同时购买尿布和啤酒,但是先购买了啤酒再买尿布的置信度比先买尿布再买啤酒的置信度要大,说明如果我们通过一定的营销策略让顾客有很强的意愿购买啤酒,那么他们100%会再去买尿布,这样的话我们可以降低啤酒的价格,明着看是在促销啤酒 ,实际上是为了销售价格更高的尿布,从而有效的提高整体的收入。
Apriori算法原理
在寻找频繁项集的时候,最简单的方法就是暴力的方法,但是假设一个包含K个项的项集,就可能会产生 2 K − 1 2^K-1 2K−1个频繁项集,这在数据量极大的情况下是无法操作的。
那怎么解决这种要搜索的可能频繁项集太多的问题呢?Apriori算法就是一个很好的选择!Apriori算法之所叫"apriori"(先验的),是因为它用到了两条先验知识来压缩搜索空间:
-
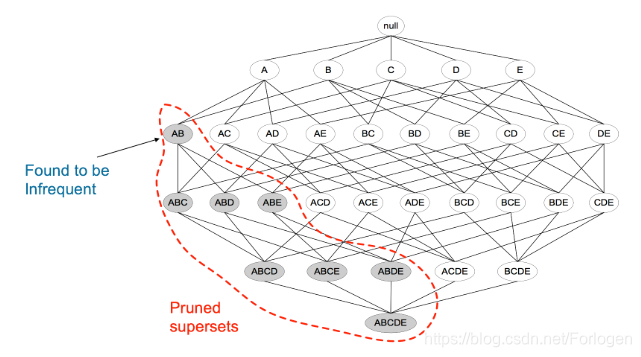
频繁项集的所有非空子项集也一定是频繁的,如下图所示,如果{A,C,E}是频繁项集,则它的子项集{A,C}{A,E}{C,E}{A}{C}{E}自然也是频繁项集,否则就会与下面的定律互相矛盾
-
一个项集不是频繁项集,则它的任意的超项集也必然不是频繁项集,这种性质叫做“反单调性”。如下图所示,当{A,B}不是频繁项集,则再加入任何一个项组成的超项集也必然不会是频繁项集,从而下面的情况就不必再考虑,有效的减少了搜索的空间
Apriori算法的伪代码描述:
伪代码描述:
// 找出频繁 1 项集
L1 =find_frequent_1-itemsets(D);
For(k=2;Lk-1 !=null;k++){
// 产生候选,并剪枝
Ck =apriori_gen(Lk-1 );
// 扫描 D 进行候选计数
For each 事务t in D{
Ct =subset(Ck,t); // 得到 t 的子集
For each 候选 c 属于 Ct
c.count++;
}
//返回候选项集中不小于最小支持度的项集
Lk ={c 属于 Ck | c.count>=min_sup}
}
Return L= 所有的频繁集;
第一步:连接(join)
Procedure apriori_gen (Lk-1 :frequent(k-1)-itemsets)
For each 项集 l1 属于 Lk-1
For each 项集 l2 属于 Lk-1
If( (l1 [1]=l2 [1])&&( l1 [2]=l2 [2])&& ……&& (l1 [k-2]=l2 [k-2])&&(l1 [k-1]<l2 [k-1]) )
then{
c = l1 连接 l2 // 连接步:产生候选
//若k-1项集中已经存在子集c则进行剪枝
if has_infrequent_subset(c, Lk-1 ) then
delete c; // 剪枝步:删除非频繁候选
else add c to Ck;
}
Return Ck;
第二步:剪枝(prune)
Procedure has_infrequent_sub (c:candidate k-itemset; Lk-1 :frequent(k-1)-itemsets)
For each (k-1)-subset s of c
If s 不属于 Lk-1 then
Return true;
Return false;
从Apriori算法的伪代码总结基本的流程如下所示:
- 输入:数据集合D、最小支持度α
- 输出:最大的频繁k项集。
(1)扫描数据集,得到所有出现过的数据,作为候选1项集
(2)挖掘频繁k项集
- 扫描计算候选k项集的支持度
- 剪枝去掉候选k项集中支持度低于最小支持度α的数据集,得到频繁k项集。如果频繁k项集为空,则返回频繁k-1项集的集合作为算法结果,算法结束。如果得到的频繁k项集只有一项,则直接返回频繁k项集的集合作为算法结果,算法结束
- 基于频繁k项集,连接生成候选k+1项集
(3)利用步骤2,迭代得到k=k+1项集结果
实例
下面我们通过一个小例子来看一下Apriori算法是如何执行的。
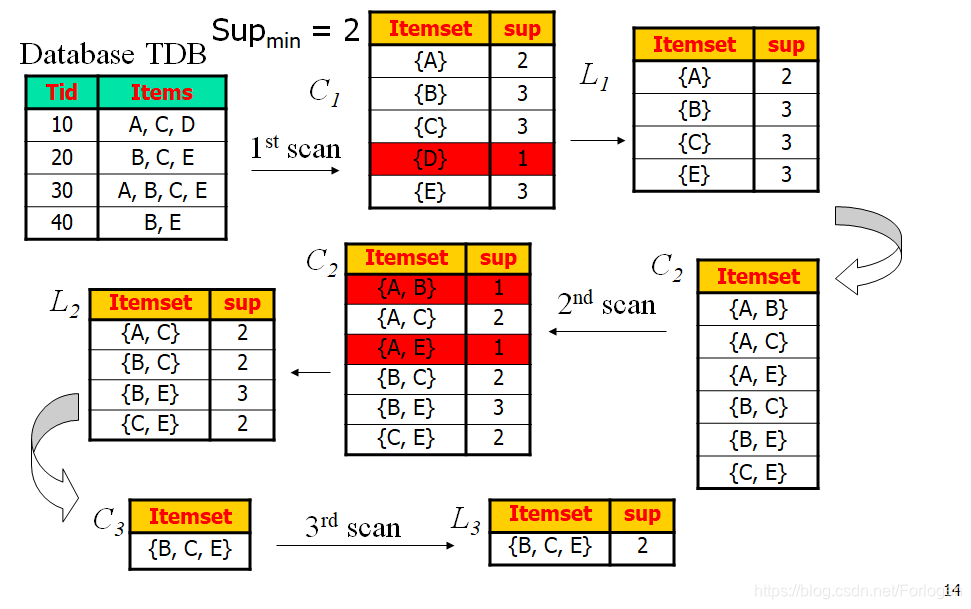
- 假设最开始我们的事务集中有TID标号为10,20,30,40四条事务,其中的所包含的项集为{A,C,D}、{B,C,E}、{A,B,C,E}、{B,E},所设置的最小支持度为 m i n s u p = 2 min{sup} = 2 minsup=2
- 扫描事务集,找出所有的候选1项集C1,其中{D}的支持度小于 m i n s u p min{sup} minsup ,故将其剪枝得到频繁一项集L1
- 对L1做连接操作得到候选2项集C2。同样进行扫描,其中{A,B}、{A,E}支持度小于 m i n s u p min{sup} minsup,故将其剪枝得到频繁二项集L2
- 对L2做连接操作,可能得到的子项有{A,B,C}、{A,C,E}、{A,B,C,E}、{B,C,E},但{A,B,C}、{A,C,E}、{A,B,C,E}的子项集{A,B}、{A,E}不是频繁项集,所以它们必然也不是频繁项集将其剪枝,得到频繁3项集L3
- 对L3进行连接操作得到的结果为空,故算法终止,所有的频繁项集为{B,C,E}
关联规则的产生
上面通过Apriori算法产生了频繁项集,我们使用它就可以产生强关联规则。因为在产生频繁项集的过程中所有的项都已满足了最小支持度,故这里只需要考虑满足最小置信度即可。最小置信度的公司如下所示 C o n f i d e n c e ( A ⇒ B ) = P ( B ∣ A ) = s u p p o r t ( A B ) s u p p o r t ( A ) = s u p p o r t − c o u n t ( A B ) s u p p o r t − c o u n t ( A ) Confidence(A\Rightarrow B) = P(B|A)= \frac{support(AB)}{support(A)} = \frac{support - count(AB)}{support-count(A)} Confidence(A⇒B)=P(B∣A)=support(A)support(AB)=support−count(A)support−count(AB)从中可以看出,最小置信度的值可以由最小支持度的值得出,因此关联规则的产生过程可以总结为:
- 对于所有的频繁项集 l l l产生它的所有非空子项集 s s s
- 考察 L i L_{i} Li中每个子项集 s s s,计算 s u p p o r t − c o u n t ( l ) s u p p o r t − c o u n t ( s ) \frac{support-count(l)}{support-count(s)} support−count(s)support−count(l),如果它的值大于最小置信度 m i n c o n f min_{conf} minconf,则输出强关联规则 S ⇒ ( l − s ) S\Rightarrow (l - s) S⇒(l−s)
例如上面的例子中产生的频繁项集为{B,C,E},它的所有非空子集为{B,C}、{B,E}、{C,E}、{B}、{C}、{E},那么可以产生的关联规则如下所示:
c o n f i d e n c e ( B , C ⇒ E ) = 2 2 confidence({B,C}\Rightarrow {E})=\frac{2}{2} confidence(B,C⇒E)=22 = 100%
c o n f i d e n c e ( B , E ⇒ C ) = 2 3 confidence({B,E}\Rightarrow {C})=\frac{2}{3} confidence(B,E⇒C)=32 = 66%
c o n f i d e n c e ( C , E ⇒ B ) = 2 2 confidence({C,E}\Rightarrow {B})=\frac{2}{2} confidence(C,E⇒B)=22 = 100%
c o n f i d e n c e ( B ⇒ C , E ) = 2 3 confidence({B}\Rightarrow {C,E})=\frac{2}{3} confidence(B⇒C,E)=32 = 66%
c o n f i d e n c e ( C ⇒ B , E ) = 2 3 confidence({C}\Rightarrow {B,E})=\frac{2}{3} confidence(C⇒B,E)=32 = 66%
c o n f i d e n c e ( E ⇒ B , C ) = 2 3 confidence({E}\Rightarrow {B,C})=\frac{2}{3} confidence(E⇒B,C)=32 = 66%
如果最小置信度设置为50%,则以上的关联规则就都是强关联规则;若最小置信度为70%,则第1条和第3条属于强关联规则。
改进
在Apriori算法中,在每次产生频繁项集的过程中,每次都要扫描整个的事务数据库你,而且会产生数目庞大的候选集,导致在计算候选集的支持度时计算量巨大,很大程度上影响了算法的效率。因此我们需要找到一些方法来缓解这个问题。主要的思路有:减少事务数据库的扫描次数、压缩候选集的数目、提高候选集支持度计数的效率等。
下面主要介绍几种不同的提高Apriori算法的方法,至于FP-growth算法再单独介绍吧。
-
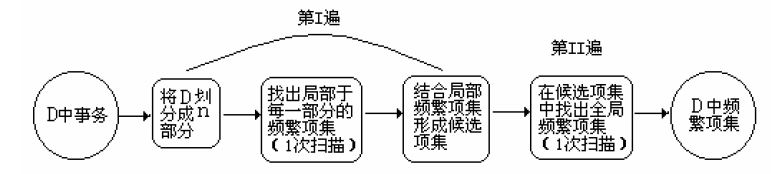
划分
根据一条原则:事务数据库D的任何频繁项集必须作为局部频繁项集至少出现在一个分区中,这是显然成立的。因此我们将事务数据库划分为n个非重叠的分区,对于每个分区找出局部频繁项集;然后再次扫描数据库,评估每个候选集的支持度,从而最后确定全局的频繁项集。
-
抽样
对于事务数据库随机抽样,产生样本S,然后在其中搜索频繁项集。这样因为我们抽样得到的只是一部分数据,所以会在一定程度上丢失一些全局频繁项集。为了解决这个缺陷,我们可以使用更小的最小支持度阈值,在S上来找到更多的频繁项集,从而尽可能的保证少丢失;或者再次扫描数据库,找到丢失的频繁模式。 -
DIC:动态项集计数
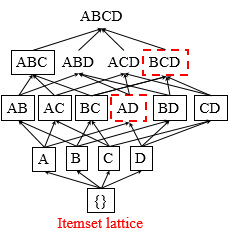
它不是像Appriori算法那样在完整的扫描完数据库之前确定每一次的频繁K项集,而是可以在任何开始点添加新的候选项集。如果一个项集的所有子项集都已被确定是频繁的,那么添加它为新的候选,这样会减少扫描数据库的次数。
以上图为例,在第一次扫描完数据库后确定了{A}、{B}、{C}、{D}为频繁1项集,那么我们就可以提前看AD是否是频繁二项集,而不必等到产生了完整的候选2项集后再去看它是否是频繁2项集。
参考:
《数据挖掘概念与技术》第6章 挖掘频繁模式、关联和相关性:基本概念和方法





















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








