Coarse-Grain Fine-Grain Coattention Network for Multi-Evidence Question Answering

本文链接：https://blog.youkuaiyun.com/Forlogen/article/details/103171853

ICLR 2019 Coarse-Grain Fine-Grain Coattention Network for Multi-Evidence Question Answering

背景

本篇文章所关注的问题是机器阅读理解（Machine Reading Comprehension），即根据查询在给定的文档中寻找相应答案的部分，具体来说是多事实QA（multi-evidence QA）问题。现有的端到端模型在单文档QA问题上往往可以取得不错的效果，即此时文档较短，且查询对应的答案存在于文档的某一具体区域。但是当查询所涉及的文档较多，且文档所对应的evidence散落在多文档的多个部分时，已有的模型处理起来就有点吃力了。

为了解决上述存在的问题，作者在本文中提出了一种Coarse-Grain Fine-Grain Coattention Network （CFC），它以一种从粗粒度到细粒度的渐进的方式来寻找查询所对应的答案部分。模型整体上包括两部分：

coarse-grain module：根据给定的查询和相应的文档通过coattention建立一种粗粒度的表示，然后通过自注意力进行总结，此时它是不知道候选答案的
gine-grain module：通过比较查询在所有文档中出现候选答案的上下文来为每个答案打分，通过coattention建立关于候选答案所在上下文和问题的表示

在两个模块中均使用了层次化的coattention以及自注意力机制（self-attention）,模型通过这两种注意力机制实现查询、支持文档和候选答案之间不同部分的关注。

CFC在WikiHop的测试集上取得了70.6%的准确率，在没有使用预训练编码器的情况下，以3%的优势好于现有的SOTA模型；另外在TriviaQA上也取得了更好的效果，从而证明了所提出模型的有效性和优越性。

模型

CFC模型整体上如下图所示：

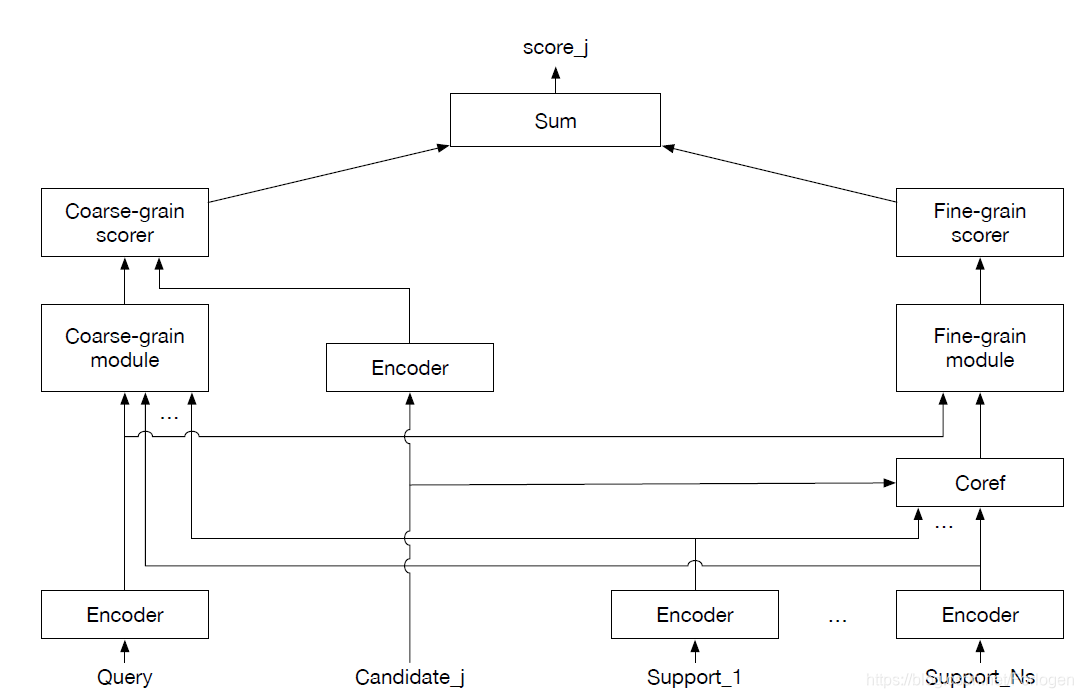
小声说：这是我看过这么多文章种画的最朴实的模型图了~

模型图一目了然，整体上包含上述的两个模块，它们分别处理查询（query）、和支持文档（support docs）。从这里可以看到两个模块都包含对应的打分器（scorer），最后综合考虑两部分的分数来选择问题对应的答案。

Coarse-grain module

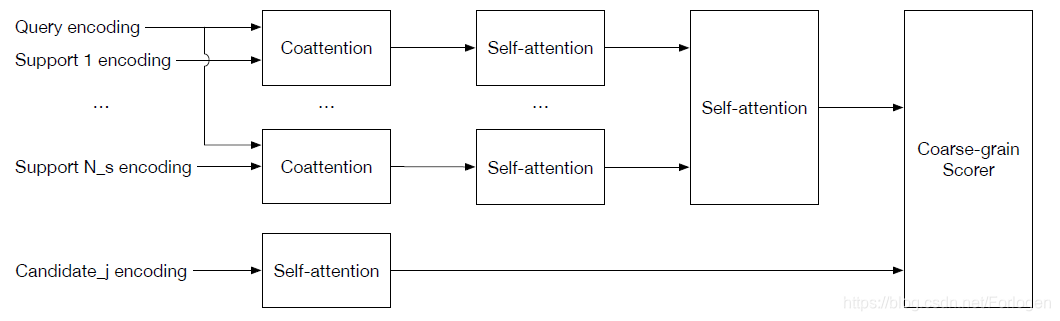
假设当前给定的查询为 $q$ ，支持文档集为 $N_{s}$ ，候选答案集为 $N_{c}$ 。首先通过Bi-GRU对各部分进行编码，其中查询、第 $i$ 个文档和第 $j$ 个候选答案所对应的表示向量为 $L_{q}$ 、 $L_{s}$ 和 $L_{c}$ 。
$E_{q}=\text{BiGRU}(\tanh (W_{q}L_{q}+b_{q})) \\ E_{s}=\text{BiGRU}(L_{s}) \\ E_{c}=\text{BiGRU}(L_{c})$
从上图中可以看出，首先 $E_{s}$ 和 $E_{q}$ 使用coattention来建立表示向量，再使用self-attention来和 $E_{c}$ 进行比较，从而完成最后的打分操作。

具体的过程为：在得到了如上的表示向量后，首先使用 $E_{s}$ 和 $E_{q}$ 计算一个亲和度矩阵（affinity matrix） $A=E_{s}(E_{q})^T$
那么 $E_{s}$ 和 $E_{q}$ 就可以通过 $A$ 得到各自对应的summary vector：
$S_{s}= \text{softmax}(A)E_{q} \\ S_{q}= \text{softmax}(A^T)E_{s}$
然后通过Bi-GRU得到文档的上下文向量 $C_{s}=\text{BiGRU}(S_{q}\text{softmax}(A))$ 最后将 $C_{s}$ 和 $S_{s}$ 进行拼接得到 $U_{s}=[C_{s}:S_{s}]$

以上过程可以简单的表述为 $\text{Coattn}(E_{s},E_{q}) \rightarrow U_{s}$

接着使用两层的MLP来对 $U_{s}$ 的每个位置进行打分，得到 $G_{s}$ 。接着使用self-attention来为每个支持文档计算一个对应的固定长度的summary vector，使用它们和候选答案进行Coarse-grain模块的打分操作。
$G_{c}=\text{Selfattn}(E_{c}) \\ G'=\text{Selfattn}(G) \\ y_{coarse}=\tanh(W_{coarse}G'+b_{coarse})G_{c}$

Fine-grain module

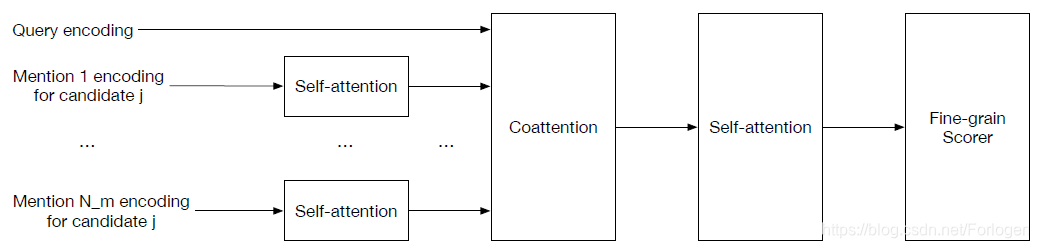
根据前面对于fine-grain模块的描述，它会根据候选答案在支持文档中找到对应的上下文部分，这里称为mention。其中每一个mention都是通过self-attention得到对应的summary vector，接着根据summary vectors和query使用coattention来计算一个coattention context，最后使用self-attention来对每个mention进行打分。

假设第 $i$ 个文档中存在 $m$ 个mention，其中每一个mention表示为答案对应的起始和终止的索引 $i_{start}$ 和 $i_{end}$ ，那么第 $k$ 个mention可以表示为：
$M_{k}=\text{Selfattn}(E_{s}[i_{start}:i_{end}])$
对所有的mention使用self-attention就可以得到所有mention的表示序列 $M$ ，然后根据 $E_{q}$ 计算 $U_{m}$ 和 $G_{m}$
$U_{m}=\text{Coattn}(M,E_{q}) \\ G_{m}=\text{Selfattn}(U_{m})$ 最后通过一个线性层计算gine-grain模块的分数 $y_{fine}=W_{fine}G_{m}+b_{fine}$