【dfs】【树形贪心】 UVA1267 Network 【树上建基站，覆盖所有叶节点】

【dfs】【树形贪心】 UVA1267 Network 【树上建基站，覆盖所有叶节点】

Consider a tree network with n nodes where the internal nodes correspond to servers and the terminal nodes correspond to clients. The nodes are numbered from 1 to n. Among the servers, there is an original server S which provides VOD (Video On Demand) service. To ensure the quality of service for the clients, the distance from each client to the VOD server S should not exceed a certain value k. The distance from a node u to a node v in the tree is defined to be the number of edges on the path from u to v. If there is a nonempty subset C of clients such that the distance from each u in C to S is greater than k , then replicas of the VOD system have to be placed in some servers so that the distance from each client to the nearest VOD server (the original VOD system or its replica) is k or less.

Given a tree network, a server S which has VOD system, and a positive integer k, find the minimum number of replicas necessary so that each client is within distance k from the nearest server which has the original VOD system or its replica.

For example, consider the following tree network.

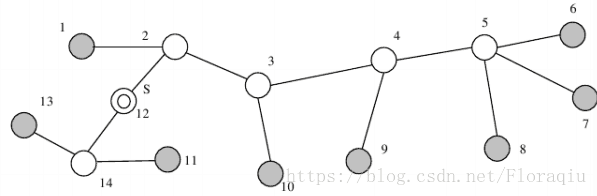
In the above tree, the set of clients is {1, 6, 7, 8, 9, 10, 11, 13}, the set of servers is {2, 3, 4, 5, 12,
14}, and the original VOD server is located at node 12.

For k = 2, the quality of service is not guaranteed with one VOD server at node 12 because the clients in {6, 7, 8, 9, 10} are away from VOD server at distance > k. Therefore, we need one or more replicas. When one replica is placed at node 4, the distance from each client to the nearest server of {12, 4} is less than or equal to 2. The minimum number of the needed replicas is one for this example.

Input
Your program is to read the input from standard input. The input consists of T test cases. The number of test cases (T) is given in the first line of the input. The first line of each test case contains an integer n (3 ≤ n ≤ 1, 000) which is the number of nodes of the tree network. The next line contains two integers s (1 ≤ s ≤ n) and k (k ≥ 1) where s is the VOD server and k is the distance value for ensuring the quality of service. In the following n − 1 lines, each line contains a pair of nodes which represent an edge of the tree network.

Output
Your program is to write to standard output. Print exactly one line for each test case. The line should contain an integer that is the minimum number of the needed replicas.

Sample Input
2
14
12 2
1 2
2 3
3 4
4 5
5 6
7 5
8 5
4 9
10 3
2 12
12 14
13 14
14 11
14
3 4
1 2
2 3
3 4
4 5
5 6
7 5
8 5
4 9
10 3
2 12
12 14
13 14
14 11

Sample Output
1
0

题意：
有n个点，其中一个为信号发射站，其覆盖范围为k，要使得每一个叶子节点能够接受到信号，问至少需要建立多少个中间基站。
PS：
注意，本题只需要覆盖叶子，而不需要覆盖中间结点，而且深度不超过k的叶子已经被原始服务器覆盖。

思路：
这里有层次关系但没有给出根，考虑无根树转有根树，且初始给定一个站，非常完美的根节点。那么此时问题转化为只需考虑深度大于K 的结点。

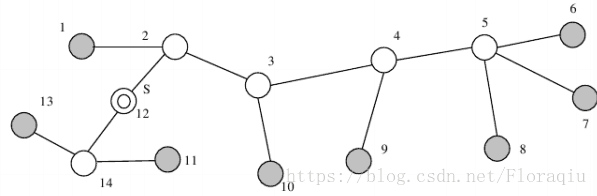
接下来，我们考虑深度最大的结点。比如结点8，应该在哪里放新的服务器来覆盖（“覆盖”一个叶子是指到该叶子的距离不超过k）它呢？只有结点5和结点4满足条件。显然，结点4比结点5划算，因为结点5所覆盖的叶子（6, 7, 8）都能被结点4所覆盖。一般的，对于深度最大的结点u，选择u的k级祖先是最划算的（父亲是1级祖先，父亲的父亲是2级祖先，以此类推）。

此时容易想到必须从深度最深的结点往上搜索才能得到最优解，我们可以先通过DFS 预处理出每个结点的深度，然后对于每个深度大于K 的叶节点（从下往上）都进行一次判断，如果未被覆盖，则找到与其距离为K 的上层结点A，更新答案，再对节点A 进DFS ，把所有与其距离小于等于K 的结点打上标记，依次进行即可。

AC代码：

#include <iostream>
#include <stdio.h>
#include <string.h>
#include <string>
#include <vector>
#include <stack>
#include <algorithm>
#include <math.h>
#define INF 0x3f3f3f3f

using namespace std;

const int maxn = 1005;
vector<int> G[maxn], dep[maxn];
int n, beg, k, vis[maxn], fa[maxn], ok[maxn], ans;

void dfs(int x, int d)//以x为根节点，处理深度
{
    if(d <= k)
        ok[x] = 1;
    vis[x] = 1;
    if(G[x].size() == 1)//记录每一个深度的叶节点
        dep[d].push_back(x);
    for(int i = 0; i < G[x].size(); i++)
    {
        int p = G[x][i];
        if(!vis[p])
        {
            fa[p] = x;
            dfs(p, d + 1);
        }
    }
//      dep[d].push_back(x);
}

void dfs2(int x, int d)//以x为根节点（基站）
{
    if(d > k)
        return ;
    ok[x] = 1;//深度不大k的节点都标记覆盖
    vis[x] = 1;
    for(int i = 0; i < G[x].size(); i++)
    {
        int p = G[x][i];
        if(!vis[p])
            dfs2(p, d + 1);
    }
}


int main()
{
    int t;
    scanf("%d", &t);
    while(t--)
    {
        //初始化工作
        ans = 0;
        memset(fa, 0, sizeof(fa));
        memset(vis, 0, sizeof(vis));
        memset(ok, 0, sizeof(ok));
        scanf("%d%d%d", &n, &beg, &k);
        for(int i = 1; i <= n; i++)
        {
            G[i].clear();
            dep[i].clear();
        }
        int v, u;
        for(int i = 1; i <= n - 1; i++)//建树
        {
            scanf("%d%d", &v, &u);
            G[u].push_back(v);
            G[v].push_back(u);
        }
        dfs(beg, 0);//处理出各节点深度
        for(int dp = n - 1; dp > k; dp--)//遍历每一个深度
        {
            for(int i = 0; i < dep[dp].size(); i++)//找到该深度下的叶节点
            {
                int p = dep[dp][i];
                if(!ok[p])//如果该叶节点没有被覆盖，则建基站
                {
                    int f = p;
                    for(int j = 0; j < k; j++)//找到其k级祖先f
                        f = fa[f];
                    ans++;//建站
                    memset(vis, 0, sizeof(vis));//先清空vis
                    dfs2(f, 0);//将以f为根节点（基站），周围深度不大于k的节点都标记覆盖
                }
            }
        }
        printf("%d\n", ans);
    }
    return 0;
}