本文介绍了全连接神经网络的基本概念，包括回归问题与分类问题的区别，以及神经网络中的正向传播和反向传播过程。正向传播用于计算网络的输出，反向传播则用于优化网络的权重，通过梯度下降减少损失函数。文章还讨论了激活函数如sigmoid在神经网络中的作用，并提到了训练感知机的基本方法。
问题与概述
在很长时间里，人们对于给定一组x~y求解函数
y
=
f
(
x
)
y=f(x)
y=f(x)一直有各种各样的研究，长期以来，人们依赖于数学方法求解计算，但是当计算机快速发展，人们的求解工具也在逐步进化。
接下来的文章中，我会以以下顺序讲解：
- 人们希望解决怎样的问题；
- 全连接神经网络概述；
- 正向传播如何实现；
- 反向传播如何实现。
回归问题与分类问题
从分类的角度，可以大致分为两类问题：回归问题与拟合问题。
回归问题是给定一组x与连续的y，求解x与y的关系。
比如：给定x=[1,2,3,4,5],y=[2,4,6,7,9,10]，可以大致看出
y
=
2
x
y=2x
y=2x。
分类问题是给定一组x与离散的y，求解x与y的关系。
比如：给定x=[1,2,3,4,5,6],y=[-0.8,-1.1,-1,2,0.9,1.1]，可以大致看出
y
=
{
−
1
if
x
<
3.5
1
if
x
>
3.5
y = \begin{cases} -1 &\text{if } x<3.5 \\ 1 &\text{if } x>3.5 \end{cases}
y={−11if x<3.5if x>3.5。
通过上面的例子，不难发现这种对应关系实际上是很难确定的。
全连接神经网络
参考神经元的工作原理（实际上生物学中神经元的功能比
y
=
f
(
x
)
y=f(x)
y=f(x)更为复杂），对神经元建模，变得到左边是多组不同神经元输入，右边是多组相同的输出。
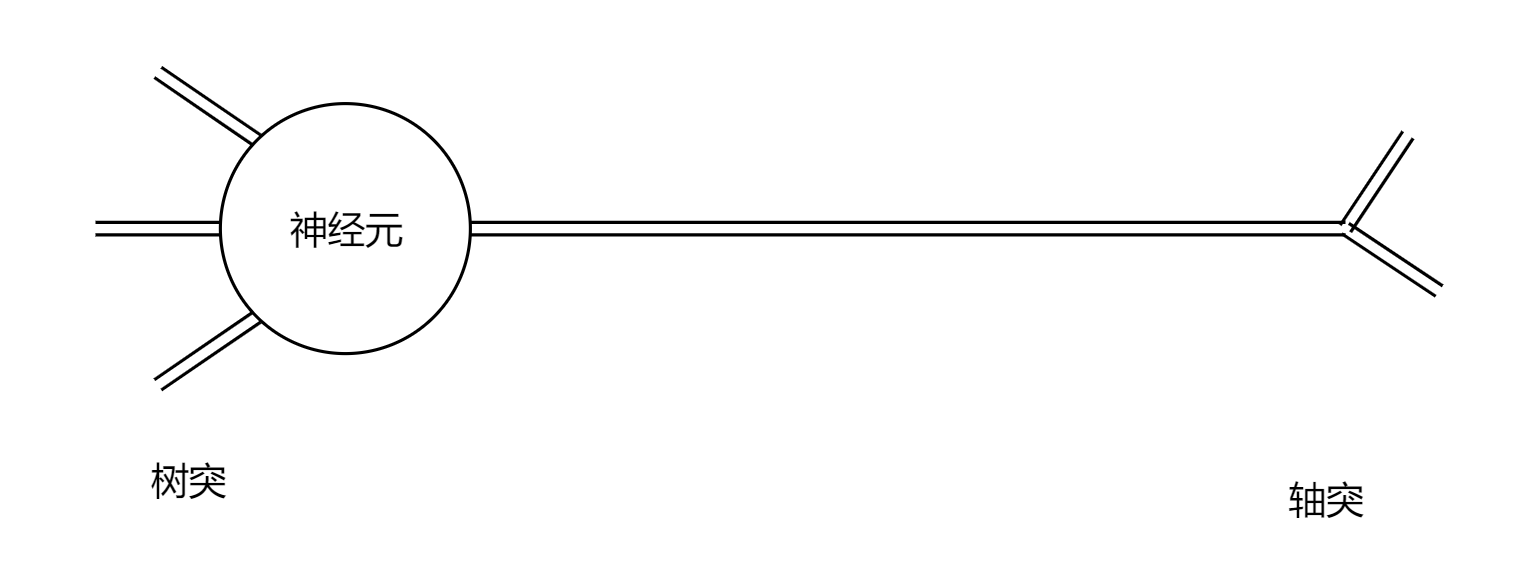
函数可变为
f
(
x
)
=
∑
(
a
i
x
i
)
+
b
f(x)=\sum_{ \begin{subarray}{l} \end{subarray}}(a_ix_i)+b
f(x)=∑(aixi)+b
可以简单的看做是对输入的加权之后增加一个偏置。
但是对于神经元来说，输出是离散的，遵循函数
y
=
{
0
if
x
<
0
1
if
x
>
=
1
y= \begin{cases} 0 &\text{if } x<0 \\ 1 &\text{if } x>=1 \end{cases}
y={01if x<0if x>=1，这种离散的特性让参数学习（求导过程）很难在计算机中进行（求导结果为0），对于某个参数的更新是通过
λ
←
λ
+
Δ
λ
\lambda\leftarrow\lambda+\Delta\lambda
λ←λ+Δλ，而求导结果为0导致了
Δ
λ
\Delta\lambda
Δλ很难求解（
Δ
λ
\Delta\lambda
Δλ永远为0），于是需要使用激活函数。最常用的激活函数是
s
i
g
m
o
i
d
(
x
)
=
1
1
+
e
−
x
sigmoid(x)=\frac{1}{1+e^{-x}}
sigmoid(x)=1+e−x1。
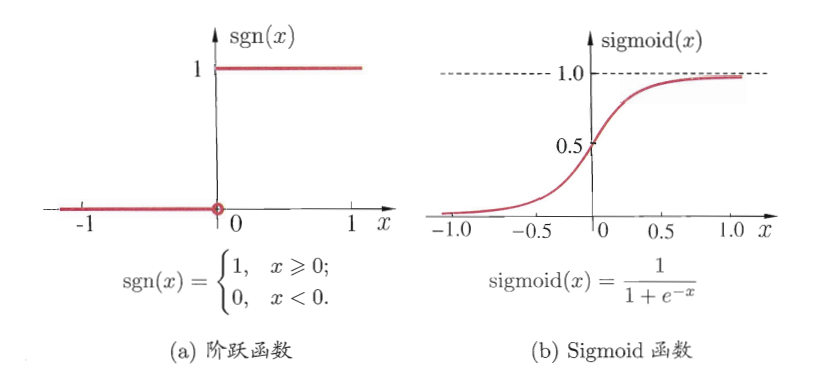
该函数有一个特点： f ′ ( x ) = f ( x ) ( 1 − f ( x ) ) f'(x)=f(x)(1-f(x)) f′(x)=f(x)(1−f(x))，这个在反向传播中需要用到。
这样一个感知机就产生了。
有效性
对于一个4分类问题，类别为 { D 1 , D 2 , D 3 , D 4 } \{D_1, D_2, D_3, D_4\} {D1,D2,D3,D4}，训练两个感知器，第一个感知机可以将类型分为 { D 1 , D 2 } , { D 3 , D 4 } \{D_1, D_2\}, \{D_3, D_4\} {D1,D2},{D3,D4}，第二个感知机可以将类型分为 { D 1 , D 4 } , { D 2 , D 3 } \{D_1, D_4\}, \{D_2, D_3\} {D1,D4},{D2,D3}，那么这两个感知机（神经元）并联一定可以直接得到类型。
训练感知机
对于训练集，构成是x~y，那么假定神经网络输出为
y
^
\hat{y}
y^，
y
^
\hat{y}
y^与真实的标签
y
y
y之间一定有误差，这时就需要一个函数
f
(
y
,
y
^
)
f(y, \hat{y})
f(y,y^)来计算其误差，也被称为损失函数。模型的训练就是减少损失函数的过程，损失函数有很多种，并且有很多介绍，在此不再赘述。
公式推导
正向传播（前向传播）
对于一个神经元，其中
a
,
b
a,b
a,b为参数
f
(
x
)
=
∑
(
a
i
x
i
)
+
b
(1)
f(x)=\sum_{ \begin{subarray}{l} \end{subarray}}(a_ix_i)+b \tag{1}
f(x)=∑(aixi)+b(1)
经过激活函数得到输出
y
^
=
s
i
g
m
o
i
d
(
f
(
x
)
)
=
s
i
g
m
o
i
d
(
∑
(
a
i
x
i
)
+
b
)
(2)
\begin{equation} \begin{split} \hat{y} &=sigmoid(f(x))\\ &=sigmoid(\sum_{ \begin{subarray}{l} \end{subarray}}(a_ix_i)+b) \end{split} \end{equation} \tag{2}
y^=sigmoid(f(x))=sigmoid(∑(aixi)+b)(2)
经过损失函数 f ( y , y ^ ) f(y, \hat{y}) f(y,y^)得到损失，假设使用均方误差作为损失函数
E k = f ( y , y ^ ) = 1 2 ∑ ( y j ^ − y j ) 2 (3) E_k=f(y, \hat{y})=\frac{1}{2}\sum_{ \begin{subarray}{l} \end{subarray}}(\hat{y_j}-y_j)^2 \tag{3} Ek=f(y,y^)=21∑(yj^−yj)2(3)
反向传播
希望求解参数 a , b a,b a,b，使用工具 a ← a + Δ a ， b ← b + Δ b a\leftarrow a+\Delta a， b\leftarrow b+\Delta b a←a+Δa，b←b+Δb，该问题变为如何求解 Δ a , Δ b \Delta a ,\Delta b Δa,Δb，我们期望从损失函数 E k = f ( y , y ^ ) E_k=f(y, \hat{y}) Ek=f(y,y^)反向推导出参数 a , b a,b a,b对应的损失 Δ a , Δ b \Delta a, \Delta b Δa,Δb。接下来就是对参数的推导。以下图神经网络为例，后面的公式推导会使用图中的变量
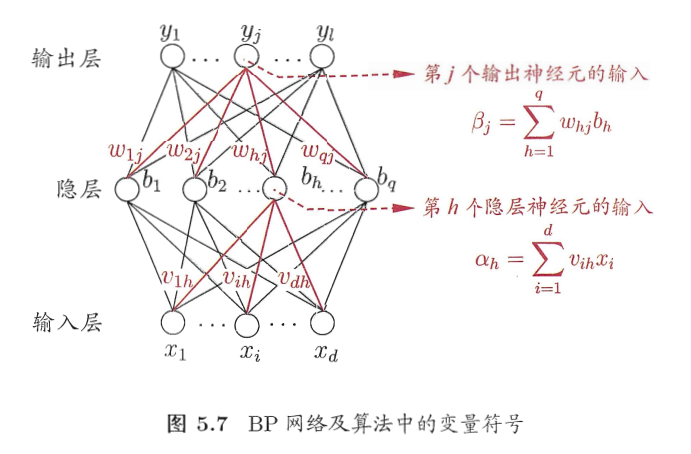
假定对于隐藏层
b
b
b的第
h
h
h个神经元
b
h
b_h
bh收到的输入为
α
h
=
∑
(
v
i
h
x
i
)
(4)
\alpha_h=\sum_{ \begin{subarray}{l} \end{subarray}}(v_{ih}x_i)\tag{4}
αh=∑(vihxi)(4)
输出层第
j
j
j个神经元
y
j
y_j
yj收到的输入为
β
j
=
∑
(
w
h
j
b
h
)
(5)
\beta_j=\sum_{ \begin{subarray}{l} \end{subarray}}(w_{hj}b_h)\tag{5}
βj=∑(whjbh)(5)
w h j w_{hj} whj为神经元 b h b_h bh的输出。通过(5)式可得到
b h = ∂ β j ∂ w h j (6) b_h=\frac{\partial\beta_j}{\partial w_{hj}}\tag{6} bh=∂whj∂βj(6)
BP算法基于梯度下降算法，以目标的负梯度方向对参数进行调整，给定学习率 η \eta η，有
Δ w h j = − η ∂ E k ∂ w h j (7) \Delta w_{hj}=-\eta\frac{\partial E_k}{\partial w_{hj}}\tag{7} Δwhj=−η∂whj∂Ek(7)
展开
∂ E k ∂ w h j = ∂ E k ∂ y j ^ ⋅ ∂ y j ^ ∂ β j ⋅ ∂ β j ∂ w h j (8) \frac{\partial E_k}{\partial w_{hj}}=\frac{\partial E_k}{\partial\hat{y_j}}\cdot\frac{\partial\hat{y_j}}{\partial \beta_j}\cdot\frac{\partial\beta_j}{\partial w_{hj}}\tag{8} ∂whj∂Ek=∂yj^∂Ek⋅∂βj∂yj^⋅∂whj∂βj(8)
先看前两项，相当于对 ∂ s i g m o i d ( E k ) = ∂ E k ∂ s i g m o i d ( E k ) \partial sigmoid(E_k)=\partial E_k\partial sigmoid(E_k) ∂sigmoid(Ek)=∂Ek∂sigmoid(Ek)求导
∂ E k ∂ y j ^ ⋅ ∂ y j ^ ∂ β j = ∂ E k ∂ β j = y j ^ ( y j ^ − 1 ) ( y j − y j ^ ) (9) \frac{\partial E_k}{\partial\hat{y_j}}\cdot\frac{\partial\hat{y_j}}{\partial \beta_j}=\frac{\partial E_k}{\partial \beta_j}=\hat{y_j}(\hat{y_j}-1)(y_j-\hat{y_j})\tag{9} ∂yj^∂Ek⋅∂βj∂yj^=∂βj∂Ek=yj^(yj^−1)(yj−yj^)(9)
结合式(6)(7)(8)(9)可以得到
Δ w h j = − η y j ^ ( y j ^ − 1 ) ( y j − y j ^ ) b h (10) \Delta w_{hj}=-\eta\hat{y_j}(\hat{y_j}-1)(y_j-\hat{y_j})b_h\tag{10} Δwhj=−ηyj^(yj^−1)(yj−yj^)bh(10)
b h b_h bh为当前轮的参数，所以是已知的。
其余的参数与此类似。
资料
拟合方法简介：
- 最小二乘法（Least Squares）：通过最小化数据点到拟合曲线的误差的平方和来拟合曲线。
- 样条插值（Spline Interpolation）：一种插值方法，通过在数据点之间建立平滑的曲线来拟合数据。
- 多项式拟合（Polynomial Regression）：基于多项式的拟合方法，用于描述两个变量之间的关系。
- 指数拟合（Exponential Regression）：基于指数函数的拟合方法。
- 对数拟合（Logarithmic Regression）：基于对数函数的拟合方法。
- 幂函数拟合（Power Regression）：基于幂函数的拟合方法。
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
