数据结构与算法
一、数据结构
1、稀疏数组
参考网址:https://www.cnblogs.com/yanzezhong/p/12449692.html
适用场景
- 经典的棋盘存储问题
- 稀疏数组写入文件
基本特点&基本思路
代码实现
/**
* 经典的棋盘存储问题
*/
public class SparseArrayDemo {
private static void sparseArray(){
//1、创建一个原始的二维数组 11*11
//0:没有棋子、1:黑子、2:白子
int[][] chessArr1 = new int[11][11] ;
chessArr1[1][2] = 1 ;
chessArr1[2][3] = 2 ;
//输出原始的二维数组
System.out.println("打印原始的二维数组:");
for (int[] row1:chessArr1){
for (int data:row1){
System.out.printf("%d\t",data);
}
System.out.println();
}
//2、将二维数组转换成稀疏数组
//(1)、获取稀疏数组的行数
int row = 0 ;
for (int[] row1:chessArr1){
for (int data:row1){
if (data != 0){
row++ ;
}
}
}
System.out.println("非零值的个数:"+row);
//(2)、创建稀疏数组
int[][] sparseArr = new int[row+1][3] ;
sparseArr[0][0] = chessArr1.length ;
sparseArr[0][1] = chessArr1[0].length ;
sparseArr[0][2] = row ;
//(3)、遍历二维数组,将非0的值存放到洗漱数组 sparseArr 中
int count = 0 ;
for (int i=0;i<chessArr1.length;i++){
for (int j=0;j<chessArr1[i].length;j++){
if (chessArr1[i][j]!=0){
count++ ;
sparseArr[count][0] = i ;
sparseArr[count][1] = j ;
sparseArr[count][2] = chessArr1[i][j] ;
}
}
}
//测试:打印 稀疏数组
System.out.println("打印稀疏数组:");
for (int[] row1:sparseArr){
for (int data: row1){
System.out.printf("%d\t",data);
}
System.out.println();
}
//3、将稀疏数组 还原成 原先的二维数组
//(1)、创建 二维数组
int[][] chessArr2 = new int[sparseArr[0][0]][sparseArr[0][1]] ;
//(2)、根据稀疏数组中的数据,映射值
for (int i = 1 ;i<sparseArr.length;i++) {
int x = sparseArr[i][0] ;
int y = sparseArr[i][1] ;
int value = sparseArr[i][2] ;
chessArr2[x][y] = value ;
}
//测试:还原 二维数组
System.out.println("通过稀疏数组后,还原的二维数组:");
for (int[] row1:chessArr2){
for (int data:row1){
System.out.printf("%d\t",data);
}
System.out.println();
}
}
}
2、队列(通过数组实现
参考网站:https://www.cnblogs.com/MWCloud/p/11239320.html
队列特点
- 可以使用数组和链表两种方式来实现。
- 遵循先入先出(FIFO)的规则,即先进入的数据先出。
- 属于有序列表。
2.1 线性队列
适用场景
基本思路

代码实现
class ArrayQueue{
private int maxSize ; //表示队列的最大容量(数组)
private int front ; //队列头
private int rear ; //队列尾
private int[] arr ; //该数组用于存放数据,模拟队列
//创建队列的构造器
public ArrayQueue(int maxSize){
this.maxSize = maxSize ;
arr = new int[maxSize] ;
front = -1 ; //指向队列头部,分析出front是指向队列头的前一个位置
rear = -1 ; //指向队列尾部,指向队列尾的数据(即是队列最后的一个数据)
}
//判断队列是否满
public boolean isFull(){
return rear == maxSize-1 ;
}
//判断队列是否为空
public boolean isEmpty(){
return rear == front ;
}
//队列添加数据
public void addQueue(int n){
//判断是否是满的
if (isFull()){
System.out.println("该队列已经满了");
return;
}
rear++ ;//让 rear 后移
arr[rear] = n ;
}
//从队列中获取数据
public int getQueue(){
//判断是否为空
if (isEmpty()){
throw new RuntimeException("队列为空,不能取数据") ;
}
front++ ; // front 向后移
return arr[front];
}
public void showAllData(){
if (isEmpty()){
System.out.println("队列为空,没有数据~~~~");
return;
}
for (int data : arr){
//System.out.printf("%d ---> ",data);
System.out.printf("arr[%d]=%d ",data,data);
}
}
//显示队列头部数据
public int showHearQueue(){
if (isEmpty()){
throw new RuntimeException("队列为空,没有数据~~~") ;
}
return arr[front+1] ;
}
//判断排列是否存在数据
public boolean isNext(){
if (isEmpty()){
return false ;
}else {
return true ;
}
}
}
2.2 环形队列
适用场景
基本思路

(last + 1)%maxSize == first
last+1是为了让指针后移,而且如果不设置为 last+1 那么一开始的时候last为0 , last % maxSize == 0,且first也为0,还没加数据就满了。
- 队列为空的条件:
first == last
- 由于判断是否满的时候: last+1 ,导致实际上可以装的数据比数组长度少 1
class CircleArrayQueue{
private int maxSize ; // 数组长度,即队列最大容量
private int first; // 头指针,控制出队操作
private int last; // 尾指针,控制入队操作
private int[] arr; // 数组类型,可以换其他的。
//构造器初始化信息
//1.队列初始化 :
public CircleArrayQueue(int maxSize){
this.maxSize = maxSize;
this.arr = new int[maxSize];
this.first = 0; //这两个可以不加,不叫也是默认为0
this.last = 0;
}
//2.判断队列是否为空:
public boolean isEmpty(){
//头指针和尾指针一样 则说明为空
return last == first;
}
/*
* 这里的 last+1 主要是为了让指针后移,特别是在队列尾部添加数据的时候,本来用last也可以判断,但
* 是一开始还没加数据的时候,如果直接用last % maxSize == first,结果是true,
* 所以为了解决指针后*移和判断是否满,用来last+1。
* 其次,因为last+1可能会导致数组指针越界,所以用取模来控制它的范
* 围,同时保证他会在一个固定的范围循环变换,也利于环形队列的实现。
*/
public boolean isFull(){
return (last + 1) % maxSize == first;
}
//4.添加数据到队列尾部:入队
public void pushData(int data){
//先判断是否满了
if(isFull()){
System.out.println("队列已经满啦~~");
return;
}
arr[last] = data;
//last+1是为了后移,取模是为了避免指针越界,同时可以让指针循环
last = (last + 1) % maxSize;
}
//5.取出队首数据:出队
public int popData(){
if (isEmpty()) {
//抛异常就可以不用返回数据了
new RuntimeException("队列为空,没有获取到数据~~");
}
//要先把first对应的数组数据保存——>first后移——>返回数据
int value = arr[first];
//first+1的操作和last+1是一样的,取模也是
first = (first+1) % maxSize;
System.out.println(value);
return value;
//如果不保存first指针 那么返回的数据就不对了
//如果直接返回数据,那first指针还没后移 也不对,所以需要使用第三方变量
}
//6.展示队列中所有数据:
public void showAllData(){
if (isEmpty()) {
System.out.println("队列为空,没有数据~~");
return;
}
// 此处i不为0,是因为有可能之前有过popData()操作,使得firs不为0,所以最好使用
// first给i动态赋值
for (int i = first; i < first+size() ; i++) {
System.out.println("arr["+i%maxSize+"]"+arr[i%maxSize]);
}
}
//7.获取队列中数据的总个数:
public int dataNum(){
//韩顺平老师的教程上是这样写,但是我理解不了..........。
return (last+maxSize-first) % maxSize;
}
public void seeFirstData(){
return arr[first];
}
}
3、链表
3.1 单链表
参考网站:https://blog.youkuaiyun.com/weixin_36605200/article/details/88804537
适用场景
基本特点
基本思路
代码实现
class Linked <T>{
//内部类
private class Node{
private T t; //数据类型
private Node next; //下一个节点信息
private Node(T t,Node next){
this.t = t;
this.next = next;
}
private Node(T t){
this(t,null);
}
}
private Node head; //头结点
private int size; //链表元素个数
//构造函数
public Linked(){
this.head = null;
this.size = 0;
}
//获取链表元素的个数
public int getSize(){
return this.size;
}
//判断链表是否为空
public boolean isEmpty(){
return this.size == 0;
}
//链表头部添加元素
public void addFirst(T t){
Node node = new Node(t) ; //新节点对象
node.next = this.head ; //将头节点的信息,赋值给新节点对象
this.size++;
//等价代码:this.head = node;
this.head = new Node(t,node.next); //给新的头节点信息,赋值
}
//向链表尾部插入元素
public void addLast(T t){
this.add(t, this.size);
}
//向链表中间插入元素
public void add(T t,int index){
if (index <0 || index >size){
throw new IllegalArgumentException("index is error");
}
if (index == 0){
this.addFirst(t);
}
Node preNode = this.head;
//找到要插入节点的前一个节点
for(int i = 0; i < index-1; i++){
preNode = preNode.next;
}
Node node = new Node(t);
//要插入的节点的下一个节点指向preNode节点的下一个节点
node.next = preNode.next;
//preNode的下一个节点指向要插入节点node
preNode.next = node;
this.size++;
}
//删除链表元素
public void remove(T t){
if(head == null){
System.out.println("无元素可删除");
return;
}
//要删除的元素与头结点的元素相同
while(head != null && head.t.equals(t)){
head = head.next;
this.size--;
}
/**
* 上面已经对头节点判别是否要进行删除
* 所以要对头结点的下一个结点进行判别
*/
Node cur = this.head;
while(cur.next != null){
if(cur.next.t.equals(t)){
this.size--;
cur.next = cur.next.next;
}
else cur = cur.next;
}
}
//删除链表第一个元素
public T removeFirst(){
if(this.head == null){
System.out.println("无元素可删除");
return null;
}
Node delNode = this.head;
this.head = this.head.next;
delNode.next =null;
this.size--;
return delNode.t;
}
//删除链表的最后一个元素
public T removeLast(){
if(this.head == null){
System.out.println("无元素可删除");
return null;
}
//只有一个元素
if(this.getSize() == 1){
return this.removeFirst();
}
Node cur = this.head; //记录当前结点
Node pre = this.head; //记录要删除结点的前一个结点
while(cur.next != null){
pre = cur;
cur = cur.next;
}
pre.next = null ;
this.size--;
return cur.t;
}
//链表中是否包含某个元素
public boolean contains(T t){
Node cur = this.head;
while(cur != null){
if(cur.t.equals(t)){
return true;
}
else cur = cur.next;
}
return false;
}
@Override
public String toString() {
StringBuilder stringBuffer = new StringBuilder();
Node cur = this.head;
while(cur != null){
stringBuffer.append(cur.t).append("->");
cur = cur.next;
}
stringBuffer.append("NULL");
return stringBuffer.toString();
}
}
总结
学链表是一种痛苦,但是痛苦并快乐着,希望能够坚持下去,把链表的全家桶都学习了,而不是这么简单的增加和删除。上述如有说的不对的地方欢迎指正!
3.2 双向链表
参考网址:https://blog.youkuaiyun.com/WeiJiFeng_/article/details/79799111
适用场景
优点
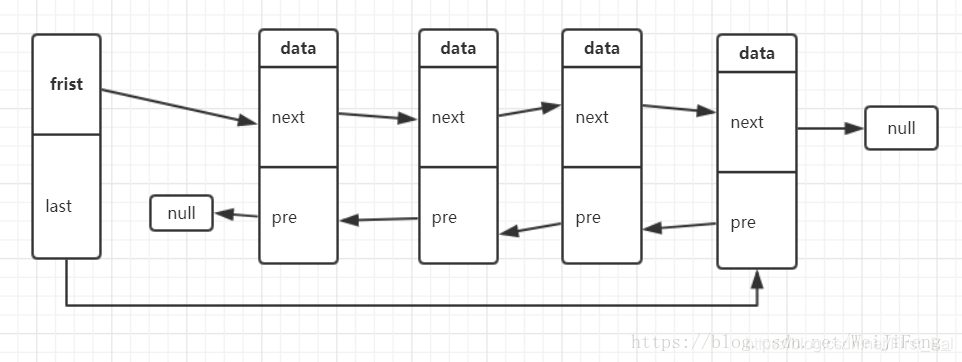
传统的链表沿着链表的反向遍历是困难的,以及操作某个节点的前一个元素,也是十分的困难。
双向链表提供了这些能力,即可以向前遍历,也可以向后遍历。其中实现在于每个链节点有两个
指向其它节点的引用。一个指向前驱节点,一个像传统链表一样指向后继节点。如图:
基本思路
- 双向链表的节点类是这样声明的:
class Link <T>{
public T val;
public Link<T> next;
public Link<T> pre;
public Link(T val) {
this.val = val;
}
}
- 插入数据
插入的新节点的next是未插入之前的frist节点。
如果链表是空的,last需要改变。如果链表非空,frist.pre字段改变。
Link<T> newLink= new Link(value);
if(isEmpty()){ // 如果链表为空
last = newLink; //last -> newLink
}else {
frist.pre = newLink; // frist.pre -> newLink
}
newLink.next = frist; // newLink -> frist
frist = newLink; // frist -> newLink
代码实现
class Link <T>{
public T val ;
public Link<T> next;
public Link<T> pre;
public Link(T val) {
this.val = val;
}
public void displayCurrentNode() {
System.out.print(val + " ");
}
}
class DoublyLinkList<T> {
private Link<T> first; //链表头部节点
private Link<T> last; //链表尾部节点
public DoublyLinkList(){
//初始化首尾指针
first = null;
last = null;
}
//判断队列是否为空
public boolean isEmpty(){
return first == null;
}
//从链表的头部添加数据
public void addFirst(T value){
Link<T> newLink= new Link(value);
if(isEmpty()){ // 如果链表为空
last = newLink; //last -> newLink
}else {
first.pre = newLink; // frist.pre -> newLink
}
newLink.next = first; // newLink -> frist
first = newLink; // frist -> newLink
}
//从链表的尾部添加数据
public void addLast(T value){
Link<T> newLink= new Link(value);
if(isEmpty()){ // 如果链表为空
first = newLink; // 表头指针直接指向新节点
}else {
last.next = newLink; //last指向的节点指向新节点
newLink.pre = last; //新节点的前驱指向last指针
}
last = newLink; // last指向新节点
}
//从某个值的前面添加数据
public boolean addBefore(T key,T value){
Link<T> cur = first;
if(first.next.val == key){
addFirst(value);
return true;
}else {
while (cur.next.val != key) {
cur = cur.next;
if(cur == null){
return false;
}
}
Link<T> newLink= new Link(value);
newLink.next = cur.next;
cur.next.pre = newLink;
newLink.pre = cur;
cur.next = newLink;
return true;
}
}
//从某个值的后添加数据
public void addAfter(T key,T value)throws RuntimeException{
Link<T> cur = first;
while(cur.val!=key){ //经过循环,cur指针指向指定节点
cur = cur.next;
if(cur == null){ // 找不到该节点
throw new RuntimeException("Node is not exists");
}
}
Link<T> newLink = new Link<>(value);
if (cur == last){ // 如果当前结点是尾节点
newLink.next = null; // 新节点指向null
last =newLink; // last指针指向新节点
}else {
newLink.next = cur.next; //新节点next指针,指向当前结点的next
cur.next.pre = newLink; //当前结点的前驱指向新节点
}
newLink.pre = cur;//当前结点的前驱指向当前结点
cur.next = newLink; //当前结点的后继指向新节点
}
//删除链表头节点
public void deleteFrist(){
if(first.next == null){
last = null;
}else {
first.next.pre = null;
}
first = first.next;
}
//删除链表靠近尾部节点的值
public void deleteLast(T key){
if(first.next == null){
first = null;
}else {
last.pre.next = null;
}
last = last.pre;
}
//删除链表中的特定值
public void deleteKey(T key)throws RuntimeException{
Link<T> cur = first;
while(cur.val!= key){
cur = cur.next;
if(cur == null){ //不存在该节点
throw new RuntimeException("Node is not exists");
}
}
if(cur == first){ // 如果frist指向的节点
first = cur.next; //frist指针后移
}else {
cur.pre.next = cur.next;//前面节点的后继指向当前节点的后一个节点
}
if(cur == last){ // 如果当前节点是尾节点
last = cur.pre; // 尾节点的前驱前移
}else {
cur.next.pre = cur.pre; //后面节点的前驱指向当前节点的前一个节点
}
}
//判断并获取 value值之前的 值
public T queryPre(T value)throws RuntimeException{
Link<T> cur = first;
if(first.val == value){
throw new RuntimeException("Not find "+value+"pre");
}
while(cur.next.val!=value){
cur = cur.next;
if(cur.next == null){
throw new RuntimeException(value +": pre is not exeist!");
}
}
return cur.val;
}
//打印所有节点信息(从前往后)
public void displayForward(){
Link<T> cur = first;
while(cur!=null){
cur.displayCurrentNode();
cur = cur.next;
}
System.out.println();
}
//打印所有节点信息(从后往前)
public void displayBackward(){
Link<T> cur = last;
while(cur!=null){
cur.displayCurrentNode();
cur = cur.pre;
}
System.out.println();
}
}
3.3 环形链表(Josephu 约瑟夫环问题)
参考网址:https://www.cnblogs.com/MWCloud/p/11241575.html
适用场景
介绍
环形链表,类似于单链表,也是一种链式存储结构,环形链表由单链表演化过来。单链表的最后一个结点的链域指向NULL,而环形链表的建立,不要专门的头结点,让最后一个结点的链域指向链表结点。 简单点说链表首位相连,组成环状数据结构。如下图结构:
基本思路
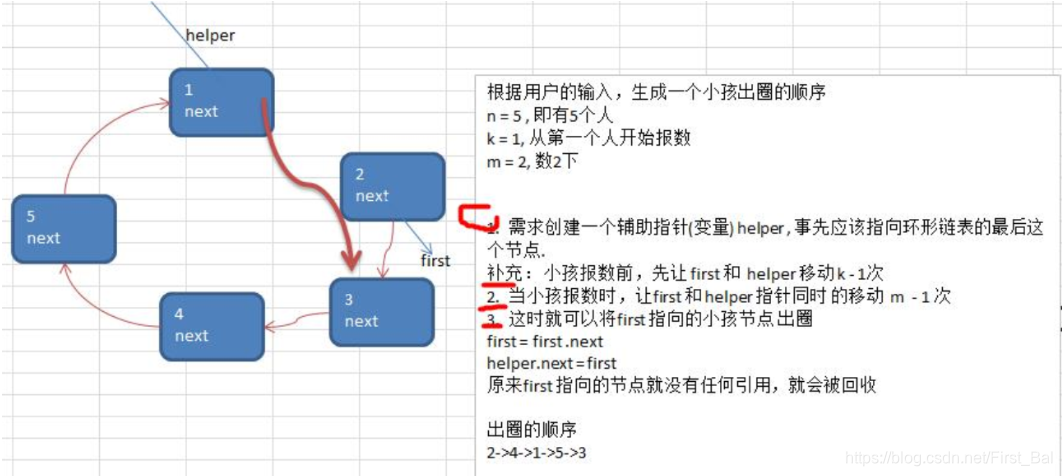
- 构建一个单向的环形链表思路
先创建第一个节点,让first指向该节点,并形成环形
后面当我们每创建一个新的节点,就把该节点加入到已有的环形链表中即可。
- 遍历环形链表
先让一个辅助指针(变量)curBoy,指向first节点
然后通过一个while循环遍历该环形链表即可,curBoy.next == first结束
代码实现
// 创建一个环形的单向链表
class CircleSingleLinkedList {
// 创建一个first节点,当前没有编号
private Boy first = null;
// 添加小孩节点,构建成一个环形的链表
public void addBoy(int nums) {
// nums 做一个数据校验
if (nums < 1) {
System.out.println("nums的值不正确");
return;
}
Boy curBoy = null; // 辅助指针,帮助构建环形链表
// 使用for来创建我们的环形链表
for (int i = 1; i <= nums; i++) {
// 根据编号,创建小孩节点
Boy boy = new Boy(i);
// 如果是第一个小孩
if (i == 1) {
first = boy;
first.setNext(first); // 构成环
curBoy = first; // 让curBoy指向第一个小孩
} else {
curBoy.setNext(boy);//
boy.setNext(first);//
curBoy = boy;
}
}
}
// 遍历当前的环形链表
public void showBoy() {
// 判断链表是否为空
if (first == null) {
System.out.println("没有任何小孩~~");
return;
}
// 因为first不能动,因此我们仍然使用一个辅助指针完成遍历
Boy curBoy = first;
while (true) {
System.out.printf("小孩的编号 %d \n", curBoy.getNo());
if (curBoy.getNext() == first) {// 说明已经遍历完毕
break;
}
curBoy = curBoy.getNext(); // curBoy后移
}
}
// 根据用户的输入,计算出小孩出圈的顺序
/**
*
* @param startNo
* 表示从第几个小孩开始数数
* @param countNum
* 表示数几下
* @param nums
* 表示最初有多少小孩在圈中
*/
public void countBoy(int startNo, int countNum, int nums) {
// 先对数据进行校验
if (first == null || startNo < 1 || startNo > nums) {
System.out.println("参数输入有误, 请重新输入");
return;
}
// 创建要给辅助指针,帮助完成小孩出圈
Boy helper = first;
// 需求创建一个辅助指针(变量) helper , 事先应该指向环形链表的最后这个节点
while (true) {
if (helper.getNext() == first) { // 说明helper指向最后小孩节点
break;
}
helper = helper.getNext();
}
//小孩报数前,先让 first 和 helper 移动 k - 1次
for(int j = 0; j < startNo - 1; j++) {
first = first.getNext();
helper = helper.getNext();
}
//当小孩报数时,让first 和 helper 指针同时 的移动 m - 1 次, 然后出圈
//这里是一个循环操作,知道圈中只有一个节点
while(true) {
if(helper == first) { //说明圈中只有一个节点
break;
}
//让 first 和 helper 指针同时 的移动 countNum - 1
for(int j = 0; j < countNum - 1; j++) {
first = first.getNext();
helper = helper.getNext();
}
//这时first指向的节点,就是要出圈的小孩节点
System.out.printf("小孩%d出圈\n", first.getNo());
//这时将first指向的小孩节点出圈
first = first.getNext();
helper.setNext(first); //
}
System.out.printf("最后留在圈中的小孩编号%d \n", first.getNo());
}
}
// 创建一个Boy类,表示一个节点
class Boy {
private int no;// 编号
private Boy next; // 指向下一个节点,默认null
public Boy(int no) {
this.no = no;
}
public int getNo() {
return no;
}
public void setNo(int no) {
this.no = no;
}
public Boy getNext() {
return next;
}
public void setNext(Boy next) {
this.next = next;
}
}
4、栈(Stack)
参考网址:
应用场景


栈结构是很基本的一种数据结构,所以栈的应用也很常见,根据栈结构“先进后出”的特点,
我们可以在很多场景中使用栈,下面我们就是使用上面我们已经实现的栈进行一些常见的应用:
- 十进制转N进制、行编辑器、校验括号是否匹配、中缀表达式转后缀表达式、表达式求值等。
- 子程序的调用:在跳往子程序前,会将下个指令的地址存到堆栈中,直到子程序执行完后再将地址取出,以回到原来的程序中。
- 处理递归调用:和子程序的调用类似,只是出了存储下一个指令的地址外,也将参数、区域变量等数据存入堆栈中。
- 逆序输出。
- 表达式的转换(中缀表达式转后缀表达式)与求值
- 二叉树的遍历。
- 图的深度优先(depth-first)搜索法。
- 数制转换:通过求余法,每次将余数进栈,最后将所有余数出栈即可。
- 括号匹配校验
- 迷宫求解
- 实现递归-汉诺塔
概念

栈是一种只允许在一端进行插入或删除的线性表。
- 栈的操作端通常被称为栈顶,另一端被称为栈底。
- 栈的插入操作称为进栈(压栈|push);栈删除操作称为出栈(弹栈|pop)。
特点
栈就像一个杯子,我们只能从杯口放和取,所以栈中的元素是“先进后出”的特点。
基本思路
代码实现
/**
* 顺序栈(SqStack)一般用数组来实现,主要有四个元素:2状态2操作。
* 2状态:栈空?;栈满?
* 2操作:压栈push;弹栈pop。
* @param <T> 数据类型
*/
class SqStack<T> {
private T data[];//用数组表示栈元素
private int maxSize;//栈空间大小(常量)
private int top;//栈顶指针(指向栈顶元素)
@SuppressWarnings("unchecked")
public SqStack(int maxSize){
this.maxSize = maxSize;
this.data = (T[]) new Object[maxSize];//泛型数组不能直接new创建,需要使用Object来创建(其实一开始也可以直接使用Object来代替泛型)
this.top = -1;//有的书中使用0,但这样会占用一个内存
}
//判断栈是否为空
public boolean isNull(){
boolean flag = this.top<=-1?true:false;
return flag;
}
//判断是否栈满
public boolean isFull(){
boolean flag = this.top==this.maxSize-1?true:false;
return flag;
}
//压栈
public boolean push(T vaule){
if(isFull()){
//栈满
return false;
}else{
data[++top] = vaule;//栈顶指针加1并赋值
return true;
}
}
//弹栈
public T pop(){
if(isNull()){
//栈为空
return null;
}else{
T value = data[top];//取出栈顶元素
--top;//栈顶指针-1
return value;
}
}
private static void test(){
//初始化栈(char类型)
SqStack<Character> stack = new SqStack<Character>(10);
//2状态
System.out.println("栈是否为空:"+stack.isNull());
System.out.println("栈是否已满:"+stack.isFull());
//2操作
//依次压栈(进栈)
stack.push('a');
stack.push('b');
stack.push('c');
//依次弹栈(出栈)
System.out.println("弹栈顺序:");
System.out.println(stack.pop());
System.out.println(stack.pop());
System.out.println(stack.pop());
System.out.println(stack.pop());
}
}
应用场景代码实现
(1)综合计算器
特点

计算思路
- 使用一个数栈存放数,使用一个符号栈存放操作运算符
- 通过一个index值(索引),来遍历我们的表达式
- 如果我们发现是一个数字,就直接入数栈
- 如果我们发现是一个符号,则分以下情况:
- 如果当前符号栈为空,就直接入栈
- 如果当前符号栈部位空,就进行比较。如果当前操作符的优先级小于或者等于栈中的操作符,就需要从数栈中pop出两个数,从符号栈中pop出一个符号,进行运算,将运算结果入数栈,经当前的操作符入符号栈。如果当前操作符的优先级大于栈中的操作符,就直接入符号栈。
- 当表达式扫描完毕,就顺序的从数栈和符号栈中pop出相应的数和符号,并进行运算。
- 最后在数栈中只有一个数字,就是表达式的结果。
代码实现
public static void main(String[] args) {
// 完成表达式的运算
String exp = "70+20*6-4";
// 创建两个栈,一个数栈一个符号栈
ArrayStack2 numStack = new ArrayStack2(10); //数字栈
ArrayStack2 operStack = new ArrayStack2(10); //符号栈
// 定义需要的相关变量
int index = 0; // 用于扫描
int num1 ;
int num2 ;
int oper ;
int res ;
char ch ; // 将每次扫描得到的char保存到ch
String keepNum = ""; // 用于拼接多位数
// 开始while循环的扫描exp
while(true) {
// 依次得到exp的每一个字符
ch = exp.charAt(index);
// 判断ch是什么,然后做相应的处理
if(operStack.isOper(ch)) { // 如果是运算符
// 判断当前的符号栈是否为空
if(!operStack.isEmpty()) {
// 如果符号栈有操作符就进行比较
// 如果当前的操作符的优先级小于或者等于栈中的操作符,就需要从数栈中pop出两个数
// 再从符号栈中pop出一个符号进行运算,将得到的结果入数栈,然后将当前的操作符入符号栈
if(operStack.priority(ch) <= operStack.priority(operStack.peek())) {
// 计算
num1 = numStack.pop();
num2 = numStack.pop();
oper = operStack.pop();
res = numStack.cal(num1, num2, oper);
// 把运算的结果入数栈
numStack.push(res);
// 把当前的操作符入符号栈
operStack.push(ch);
} else {
// 如果当前的操作符的优先级大于栈中的操作符,直接入符号栈
operStack.push(ch);
}
} else {
// 如果为空直接入符号栈
operStack.push(ch);
}
} else { // 如果是数字,则直接入数栈
// numStack.push(ch - '0');
// 分析思路
// 1. 当处理多位数时,不能发现时一个数就立即入栈,因为它可能是多位数
// 2. 在处理数字时,需要向exp的表达式的index后再看一位,如果是数就继续扫描,如果是符号才入栈
// 3. 因此我们需要定义一个字符串变量用于拼接
// 处理多位数
keepNum += ch;
// 如果ch已经是exp的最后一位就直接入栈
if (index == exp.length() - 1) {
numStack.push(Integer.parseInt(keepNum));
} else {
// 判断下一个字符是不是数字,如果是数字就继续扫描,如果是运算符则入栈
// 注意是看后一位,不是index++
if (operStack.isOper(exp.charAt(index+1))) {
// 如果后一位是运算符则入栈
numStack.push(Integer.parseInt(keepNum));
// keepNum清空
keepNum = "";
}
}
}
// index + 1,并判断是否扫描到最后
index++;
if (index >= exp.length()) {
break;
}
}
// 当表达式扫描完毕时,就顺序的从数栈和符号栈中pop出相应的数和符号并运行
while(true) {
// 如果符号栈为空,则计算到最后的结果,数栈中只有一个数字
if (operStack.isEmpty()) {
break;
} else {
num1 = numStack.pop();
num2 = numStack.pop();
oper = operStack.pop();
res = numStack.cal(num1, num2, oper);
numStack.push(res); // 入栈
}
}
// 将数栈的最后一个数字pop出就是结果
int res2 = numStack.pop();
System.out.printf("表达式 %s = %d", exp, res2);
}
(2)表达式计算
定义
- 中缀表达式:我们平时写的数学表达式一般为中缀表达式,如“5+2*(3*(3-1*2+1))”,直接拿中缀表达式直接让计算机计算表达式的结果并不能做到。
- 后缀表达式:把中缀表达表达式“5+2*(3*(3-12+1))”转化“523312-1+**+”这样的形式,就是后缀表达式。这种记法叫做后缀(postfix)或逆波兰(reverse Polish)记法。计算这个问题最容易的方法就是使用一个栈。
思路
-
遇到数字则直接压到数字栈顶。
-
遇到运算符(±*/)时,若操作符栈为空,则直接放到操作符栈顶。
2.1 若操作符栈顶元素的优先级比当前运算符的优先级小,则直接压入栈顶,否则执行步骤。
2.2 弹出数字栈顶的两个数字并弹出操作符栈顶的运算符进行运算,把运算结果压入数字栈顶,重复***2.1***和***2.2***直到当前运算符被压入操作符栈顶。
-
遇到左括号“(”时则直接压入操作符栈顶。
-
遇到右括号“)”时则依次弹出操作符栈顶的运算符运算数字栈的最顶上两个数字,直到弹出的操作符为左括号。
代码实现
import java.util.HashMap;
import java.util.Map;
import java.util.Stack;
import java.util.StringTokenizer;
import java.util.Vector;
import java.util.regex.Pattern;
public class Test {
public static void main(String args[]) {
String computeExpr = "1 + 5 * 6 + 3 * (2 + 3*2+2-1+3*3) + 10/5 - 6*1";
Test test = new Test();
double result1 = test.computeWithVector(computeExpr);
double result2 = test.computeWithStack(computeExpr);
System.out.println(result1 + "=======" + result2);
}
/**
* 利用java.util.Vector计算四则运算字符串表达式的值,如果抛出异常,则说明表达式有误,这里就没有控制
* @param computeExpr 四则运算字符串表达式
* @return 计算结果
*/
public double computeWithVector(String computeExpr) {
StringTokenizer tokenizer = new StringTokenizer(computeExpr, "+-*/()", true);
Vector<Double> nums = new Vector<Double>();
Vector<Operator> operators = new Vector<Operator>();
Map<String, Operator> computeOper = this.getComputeOper();
Operator curOper;
String currentEle;
while (tokenizer.hasMoreTokens()) {
currentEle = tokenizer.nextToken().trim();
if (!"".equals(currentEle)) {//只处理非空字符
if (this.isNum(currentEle)) { // 数字
nums.add(Double.valueOf(currentEle));
} else { // 非数字,即括号或者操作符
curOper = computeOper.get(currentEle);
if (curOper != null) { // 是运算符
// 运算列表不为空且之前的运算符优先级较高则先计算之前的优先级
while (!operators.isEmpty()
&& operators.lastElement().priority() >= curOper
.priority()) {
compute(nums, operators);
}
// 把当前运算符放在运算符队列的末端
operators.add(curOper);
} else { // 括号
if ("(".equals(currentEle)) { // 左括号时直接放入操作列表中
operators.add(Operator.BRACKETS);
} else {// 当是右括号的时候就把括号里面的内容执行了。
// 循环执行括号里面的内容直到遇到左括号为止。试想这种情况(2+5*2)
while (!operators.lastElement().equals(Operator.BRACKETS)) {
compute(nums, operators);
}
//移除左括号
operators.remove(operators.size()-1);
}
}
}
}
}
// 经过上面代码的遍历后最后的应该是nums里面剩两个数或三个数,operators里面剩一个或两个运算操作符
while (!operators.isEmpty()) {
compute(nums, operators);
}
return nums.firstElement();
}
/**
* 利用java.util.Stack计算四则运算字符串表达式的值,如果抛出异常,则说明表达式有误,这里就没有控制
* java.util.Stack其实也是继承自java.util.Vector的。
* @param computeExpr 四则运算字符串表达式
* @return 计算结果
*/
public double computeWithStack(String computeExpr) {
//把表达式用运算符、括号分割成一段一段的,并且分割后的结果包含分隔符
StringTokenizer tokenizer = new StringTokenizer(computeExpr, "+-*/()", true);
Stack<Double> numStack = new Stack<Double>(); //用来存放数字的栈
Stack<Operator> operStack = new Stack<Operator>(); //存放操作符的栈
Map<String, Operator> computeOper = this.getComputeOper(); //获取运算操作符
String currentEle; //当前元素
while (tokenizer.hasMoreTokens()) {
currentEle = tokenizer.nextToken().trim(); //去掉前后的空格
if (!"".equals(currentEle)) { //只处理非空字符
if (this.isNum(currentEle)) { //为数字时则加入到数字栈中
numStack.push(Double.valueOf(currentEle));
} else { //操作符
Operator currentOper = computeOper.get(currentEle);//获取当前运算操作符
if (currentOper != null) { //不为空时则为运算操作符
while (!operStack.empty() && operStack.peek().priority() >= currentOper.priority()) {
compute(numStack, operStack);
}
//计算完后把当前操作符加入到操作栈中
operStack.push(currentOper);
} else {//括号
if ("(".equals(currentEle)) { //左括号时加入括号操作符到栈顶
operStack.push(Operator.BRACKETS);
} else { //右括号时, 把左括号跟右括号之间剩余的运算符都执行了。
while (!operStack.peek().equals(Operator.BRACKETS)) {
compute(numStack, operStack);
}
operStack.pop();//移除栈顶的左括号
}
}
}
}
}
// 经过上面代码的遍历后最后的应该是nums里面剩两个数或三个数,operators里面剩一个或两个运算操作符
while (!operStack.empty()) {
compute(numStack, operStack);
}
return numStack.pop();
}
/**
* 判断一个字符串是否是数字类型
* @param str
* @return
*/
private boolean isNum(String str) {
String numRegex = "^\\d+(\\.\\d+)?$"; //数字的正则表达式
return Pattern.matches(numRegex, str);
}
/**
* 获取运算操作符
* @return
*/
private Map<String, Operator> getComputeOper() {
return new HashMap<String, Operator>() { // 运算符
private static final long serialVersionUID = 7706718608122369958L;
{
put("+", Operator.PLUS);
put("-", Operator.MINUS);
put("*", Operator.MULTIPLY);
put("/", Operator.DIVIDE);
}
};
}
/**
* 取nums的最后两个数字,operators的最后一个运算符进行运算,然后把运算结果再放到nums列表的末端
* @param nums
* @param operators
*/
private void compute(Vector<Double> nums, Vector<Operator> operators) {
Double num2 = nums.remove(nums.size() - 1); // 第二个数字,当前队列的最后一个数字
Double num1 = nums.remove(nums.size() - 1); // 第一个数字,当前队列的最后一个数字
Double computeResult = operators.remove(operators.size() - 1).compute(
num1, num2); // 取最后一个运算符进行计算
nums.add(computeResult); // 把计算结果重新放到队列的末端
}
/**
* 取numStack的最顶上两个数字,operStack的最顶上一个运算符进行运算,然后把运算结果再放到numStack的最顶端
* @param numStack 数字栈
* @param operStack 操作栈
*/
private void compute(Stack<Double> numStack, Stack<Operator> operStack) {
Double num2 = numStack.pop(); // 弹出数字栈最顶上的数字作为运算的第二个数字
Double num1 = numStack.pop(); // 弹出数字栈最顶上的数字作为运算的第一个数字
Double computeResult = operStack.pop().compute(
num1, num2); // 弹出操作栈最顶上的运算符进行计算
numStack.push(computeResult); // 把计算结果重新放到队列的末端
}
/**
* 运算符
*/
private enum Operator {
/**
* 加
*/
PLUS {
@Override
public int priority() {
return 1;
}
@Override
public double compute(double num1, double num2) {
return num1 + num2;
}
},
/**
* 减
*/
MINUS {
@Override
public int priority() {
return 1;
}
@Override
public double compute(double num1, double num2) {
return num1 - num2;
}
},
/**
* 乘
*/
MULTIPLY {
@Override
public int priority() {
return 2;
}
@Override
public double compute(double num1, double num2) {
return num1 * num2;
}
},
/**
* 除
*/
DIVIDE {
@Override
public int priority() {
return 2;
}
@Override
public double compute(double num1, double num2) {
return num1 / num2;
}
},
/**
* 括号
*/
BRACKETS {
@Override
public int priority() {
return 0;
}
@Override
public double compute(double num1, double num2) {
return 0;
}
};
/**
* 对应的优先级
* @return
*/
public abstract int priority();
/**
* 计算两个数对应的运算结果
* @param num1 第一个运算数
* @param num2 第二个运算数
* @return
*/
public abstract double compute(double num1, double num2);
}
}
5、 递归(Recursive)
概念
简单来说:递归,是方法自己调用自己。即,每次调用时传入不同的变量,递归有助于编程者解决复杂的问题,同时可让代码变得简洁
递归调用机制
应用场景
- 数据问题:迷宫问题(回溯问题)、八皇后问题、汉诺塔、阶乘问题、球和篮子的问题
- 算法中:快排、归并排序、二分查找、分值算法等
- 将用栈解决的问题 - > 递归代码比较简洁
递归需要遵守的重要规则

特点
应用场景代码
1. 迷宫问题(回溯问题)
问题分析

代码实现
public static boolean setWay(int[][] map , int i , int j){
if (map[6][5] == 2){ //判断是否达到了终点
//到达了终点
return true ;
}else {
//还未达到终点
if (map[i][j] == 0){ //判断(i,j)位置是否有墙
//(i,j)位置没有墙
//开始递归回溯
map[i][j] = 2 ;
//策略:下->右->上->左
if (setWay(map,i,j+1)){ //向下找
return true ;
}else if (setWay(map,i+1,j)){ //向右找
return true ;
}else if (setWay(map,i,j-1)){ //向上找
return true ;
}else if (setWay(map,i-1,j)){ //向左找
return true ;
}else {//走不通
map[i][j] = 3 ;
return false ;
}
}else {
//(i,j)位置有墙
return false ;
}
}
}
2. 八皇后问题(回溯算法)
问题介绍



代码实现
class EightQueensRecursive{
//定义一个 max 表示共有多少个皇后
private int max = 8;
//定义数组 array ,保存皇后放置位置的结果
private int[] array ;
//记录解决方案次数
private static int count = 0 ;
public EightQueensRecursive(){
array = new int[max] ;
}
public void test(){
check(0);
System.out.println("解决方案数量:"+count);
}
/**
* 放置第 n 个皇后
* 重点:
* check 是每一次递归是,进入 check 中都有 for (int i=0; i<max ; i++ ) 循环,因此会有回溯
* @param n 表示第 n 个皇后
*/
private void check(int n){
if (n == max){ //判断皇后是否放置完成
count++ ;
print();
return;
}
for (int i=0; i<max ; i++ ){
array[n] = i ;
if (judge(n)){
check(n+1);
}
}
}
/**
* 查看放置第 n 个皇后,就去检测该皇后是否和之前已经摆放的皇后冲突
* @param n 表示第 n 个皇后
* @return
*/
private boolean judge(int n){
for (int i=0 ; i<n ; i++){
//说明:
//1. array[i] == array[n] 表示第 n 个皇后是否和第 i 个皇后在同一列
//2. Math.abs(n-i) == Math.abs(array[n]-array[i]) 判断是否在同一斜线上
if (array[i] == array[n]||Math.abs(n-i) == Math.abs(array[n]-array[i])){
//发生了冲突
return false ;
}
}
return true ;
}
public void print(){
for (int x:array){
System.out.print(x+" ");
}
System.out.println();
}
}






















 856
856

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








