一、有序数组的平方(快慢指针法)
977.有序数组的平方
给你一个按 非递减顺序 排序的整数数组 nums,返回 每个数字的平方 组成的新数组,要求也按 非递减顺序 排序。
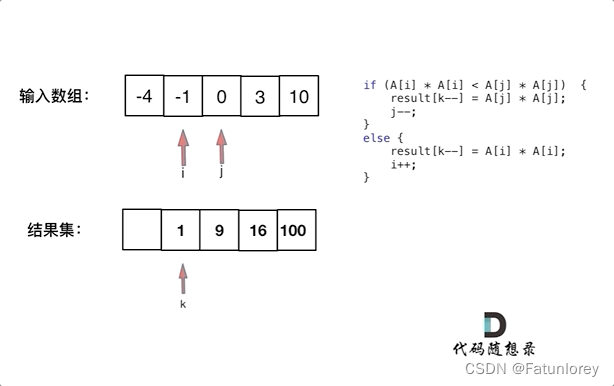
示例 1: 输入:nums = [-4,-1,0,3,10] 输出:[0,1,9,16,100] 解释:平方后,数组变为 [16,1,0,9,100],排序后,数组变为 [0,1,9,16,100]
示例 2: 输入:nums = [-7,-3,2,3,11] 输出:[4,9,9,49,121]
思路 :对于这道题我们可以选择对数组中每一个元素都进行平方,再使用快排进行排序,但是我们会发现此时的时间复杂度就为O(n+n*logn),但这并不满足题目O(n)的要求;
所以我们需要另一种思路,我们通过观察可以发现平方大的数都在数组的两边,因此我们可以使用双指针法,下面附上代码:
/**
* Note: The returned array must be malloced, assume caller calls free().
*/
int* sortedSquares(int* nums, int numsSize, int* returnSize){
*returnSize = numsSize;
int index1=0;
int index2=numsSize-1;
int *ans=(int*)malloc(sizeof(int)*numsSize);
for(int index=numsSize-1;index>=0;index--)
{
if(nums[index1]*nums[index1]>=nums[index2]*nums[index2])
{
ans[index]=nums[index1]*nums[index1];
index1++;
}
else if(nums[index1]*nums[index1]<nums[index2]*nums[index2])
{
ans[index]=nums[index2]*nums[index2];
index2--;
}
}
return ans;
}大体思路是通过定义一个大小相同的数组,不断比较两端数平方的大小以确定填入新数组的数,因为两头都是大数,所以需要新数组从最后开始填入数据。作者本人对c语言的掌握还不算熟练,再此附上自己做题时一些疑惑及解答:
a.由于最后返回的的是一个指针,即数组ans的首地址,因此其长度未知,所以为了在主函数中输出,我们需要对新数组的长度进行保存,所以就有了*returnSize=numSize这句。
main函数大致是这样:
int main(void) { int numSize; scanf("%d",&numSize); int *nums=(*int)malloc(sizeof(numSize)); for(int i=0;i<numSize;i++) scanf("%d",&num[i]); int *returnSize=NULL; int *ans=*sortfedSquares(*num,numSize,*returnSize); for(int i=0;i<(*returnSize);i++) printf("%d",ans[i]); return 0; }
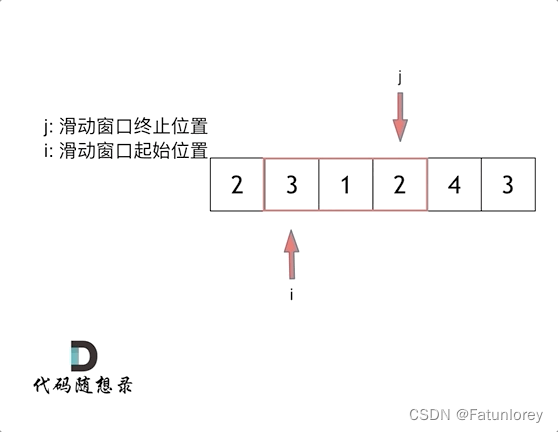
二、长度最小的子数组(滑动窗口)
给定一个含有 n 个正整数的数组和一个正整数 s ,找出该数组中满足其和 ≥ s 的长度最小的 连续 子数组,并返回其长度。如果不存在符合条件的子数组,返回 0。
示例:
输入:s = 7, nums = [2,3,1,2,4,3] 输出:2 解释:子数组 [4,3] 是该条件下的长度最小的子数组。
提示:
- 1 <= target <= 10^9
- 1 <= nums.length <= 10^5
- 1 <= nums[i] <= 10^5
a.暴力解法
思路:我们可以使用两个for循环对数组进行遍历,但这样时间复杂度将是O(n*2),代码如下:
int minSubArrayLen(int target, int* nums, int numsSize){
int sum=0;
int sub;
int min=numsSize+5;
//为了确保可以对答案进行更新,我们将其赋值为一个取不到的数
for(int left=0;left<numsSize;left++)
{
sum=0;
for(int right=left;right<numsSize;right++)
{
sum+=nums[right];
if(sum>=target)
{
sub=right-left+1;
min=min<sub?min:sub;
break;
}
}
}
min=min==numsSize+5?0:min;
return min;
}b.滑动窗口
思路:就是我们不断去移动终止位置,一旦我们找到了可以满足目标条件的终止位置,此时就可以可是缩小范围,那么此时代码的时间复杂度就降到了O(n);
int minSubArrayLen(int target, int* nums, int numsSize){
int min=numsSize+5;
int sub;
int sum=0;
int right=0,left=0;
for(;right<numsSize;right++)
{
sum+=nums[right];
while(sum>=target)
{
sub=right-left+1;
min=min<sub?min:sub;
sum-=nums[left++];
}
}
return min==numsSize+5?0:min;
}



 文章介绍了两种算法问题的解决方案:一是使用快慢指针法解决有序数组的平方问题,保持O(n)的时间复杂度;二是应用滑动窗口优化求解找到和大于等于给定值的最小子数组长度,避免双重循环,降低时间复杂度到O(n)。
文章介绍了两种算法问题的解决方案:一是使用快慢指针法解决有序数组的平方问题,保持O(n)的时间复杂度;二是应用滑动窗口优化求解找到和大于等于给定值的最小子数组长度,避免双重循环,降低时间复杂度到O(n)。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








