算法和算法分析

一、算法

特性：

        1.有穷性；（在有限步内可以结束）

        2.确定性；（相同输入有相同输出）

        3.可行性；

        4.有输入；

        5.输出；    

        考量一个算法优劣可以从时间复杂度和空间复杂度两个方面来衡量，通常情况并不存在时间复杂度和空间复杂度都好的程序。

二、时间复杂度

        时间复杂度是一个函数，它定性描述该算法的运行时间。

       算法中基本操作重复执行的次数是问题规模n的某个函数f(n)，算法的时间量度记叙T（n）=O（f（n）），它表示问题规模n的增大，算法执行时间的增长率和f（n）的增长率相同，称做算法的渐近时间复杂度，简称时间复杂度。

         这里的大O表示的是程序运行时间的上界，而通常情况下我们考虑的时间复杂度都是一般情况的时间复杂度，而非最坏情况。

 

 

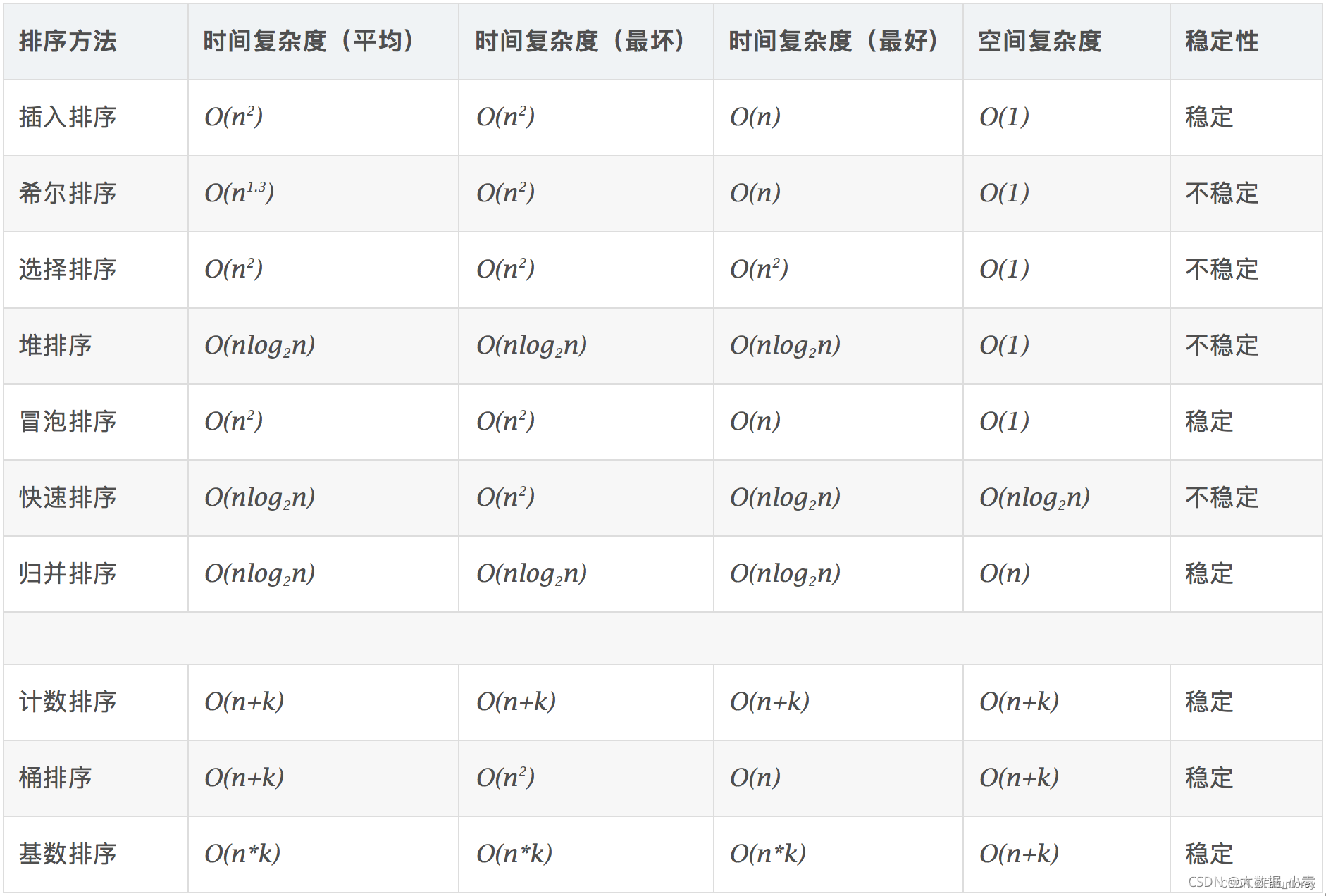
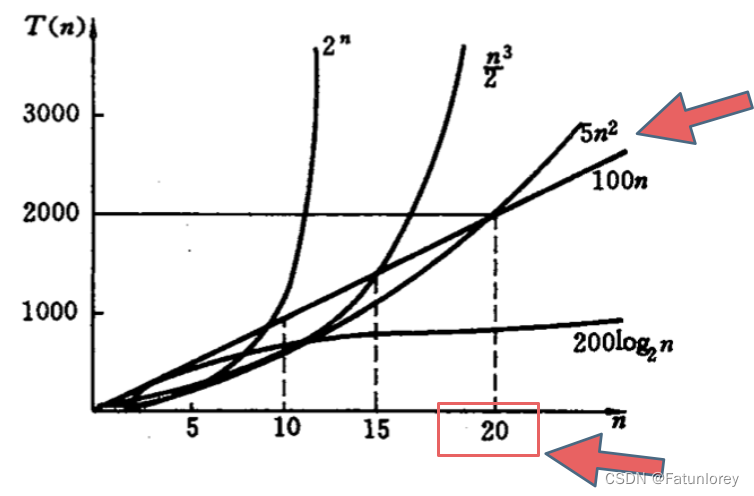
         并且在不同的规模下不同算法的所用时间也会相对变化，而时间复杂度则是在数据规模很大的情况，算法所需时间进行的数学函数模拟。时间复杂度前的系数或是次要项或是常数项，在此时由于数据规模的增大，也可以进行省略（了解极限概念的同学理解起来应该十分容易）。logn的底数对其时间复杂度，并没有影响。（代码随想录）

O(1)常数阶 < O(logn)对数阶 < O(n)线性阶 < O(n^2)平方阶 < O(n^3)立方阶 < O(2^n)指数阶

        在指数时间复杂度内可以处理则认为可以处理。关于时间复杂度的计算，即寻找重复的步骤循环（最深层的步骤）的次数即为时间复杂对大小。

递归算法的时间复杂度本质上是要看: 递归的次数 * 每次递归的时间复杂度。

三、空间复杂度

        空间复杂度是考虑程序运行时占用内存的大小，而不是可执行文件的大小。是对一个算法在运行过程中占用内存空间大小的量度，记做S(n)=O(f(n)。

  递归算法的空间复杂度 = 每次递归的空间复杂度 * 递归深度

         以递归算法为例，我们分析一下时间和空间复杂度

int fabonacci(int first,int second,int n)
{
    if(n<=0)
    return 0;
    if(n<3)
    return 1;
    if(n==3)
    return first + second;
    else
    return fabonacci(second,first+second,n-1);
}

 

 

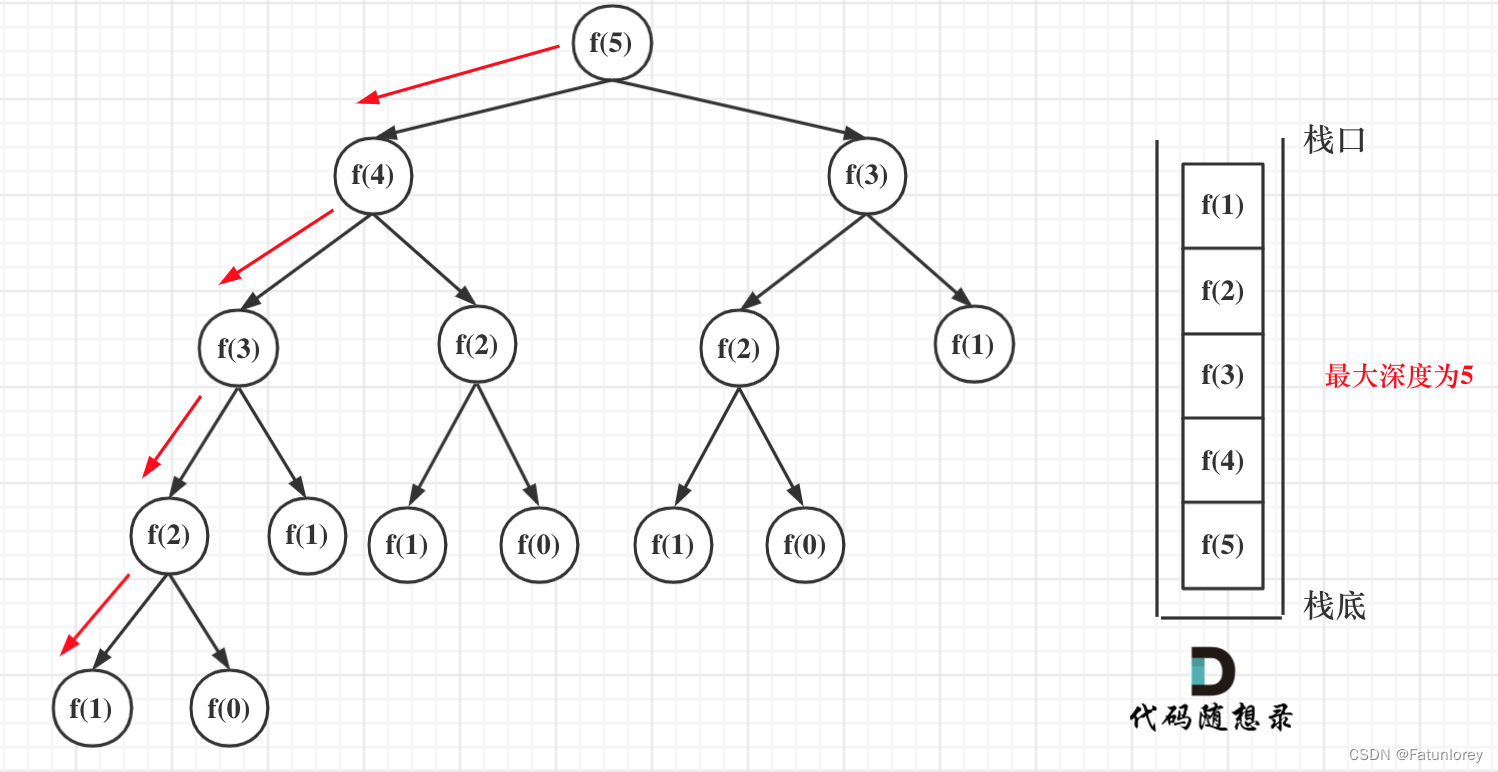
递归第n个斐波那契数的话，递归调用栈的深度就是n。那么每次递归的空间复杂度是O(1)， 调用栈深度为n，所以这段递归代码的空间复杂度就是O(n)。并且一共只递归了n次，所以时间复杂度也为O（n）。