文章目录
正交向量与子空间
向量正交:xTy=0
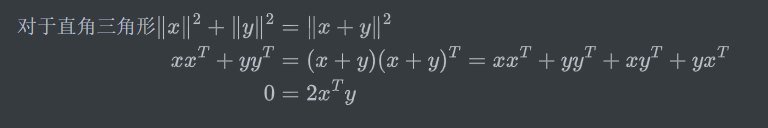
空间正交:S中每个向量与T中每个向量正交
行空间正交于零空间,同理列空间正交于左零空间

在实际应用中,数据可能会有干扰项,此时会导致Ax=b无解,使用ATAx=ATb得到最优解,去除干扰
ATA不一定可逆,如果要可逆则A的列线性无关
子空间投影
在二维空间中,p是b在a上最接近a的向量(投影):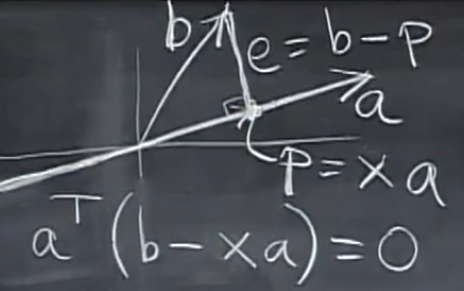
化简得
a T b = x a T a x = a T b a T a 代入得 p = a a T b a T a \begin{aligned} a^Tb &= xa^Ta\\ x &= \frac{a^Tb}{a^Ta}\\ 代入得 &p=a\frac{a^Tb}{a^Ta} \end{aligned} aTbx代入得=xaTa=aTaaTbp=aaTaaTb
b翻倍p也翻倍,a翻倍p不变
投影是由矩阵完成的(投影矩阵):
p = P b 根据 p = a a T b a T a 得: P = a a T a T a p=Pb\\ 根据p=a\frac{a^Tb}{a^Ta}得:P=\frac{aa^T}{a^Ta} p=Pb根据p=aaTaaTb得:P=aTaaaT
aTa是数字,aaT是列向量乘行向量
这个矩阵的列空间C§=a所在的直线,因为这个矩阵乘b变成了b在a直线的投影
rank§=1,因为P由列乘行产生,这一个列是列空间的基
P是对称矩阵,转置是它自己
P2=P,再投影一次不变
为什么做投影:因为Ax=b可能无解,此时只能求解最接近的那个可解问题Ax=p,p即是b在列空间的投影
在三维空间中: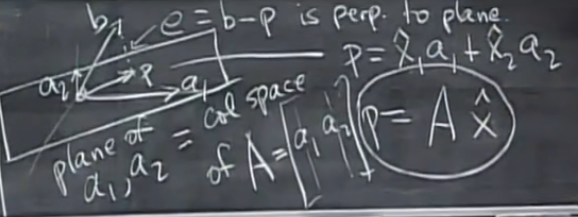
空间中平面由a1,a2两基向量产生,A=[a1 a2],b在平面上的投影为p,需要求出x使得Ax=p
e=b-Ax,e垂直于平面(也就垂直于a1和a2)
a 1 T ( b − A x ) = 0 a 2 T ( b − A x ) = 0 整理成矩阵: A T e = [ a 1 T a 2 T ] ( b − A x ) = [ 0 0 ] a_1^T(b-Ax)=0 \\ a_2^T(b-Ax)=0 \\ 整理成矩阵: A^Te= \begin{bmatrix} a_1^T\\ a_2^T \end{bmatrix} (b-Ax)= \begin{bmatrix} 0\\ 0 \end{bmatrix} a1T(b−Ax)=0a2T(b−Ax)=0整理成矩阵:ATe=[a1Ta2T](b−Ax)=[00]
e位于A的转置的零空间,因为左零空间正交于列空间,所以e垂直于A的列空间
A T A x = A T b x = ( A T A ) − 1 A T b 代入得 p = A x = A ( A T A ) − 1 A T b \begin{aligned} A^TAx &= A^Tb\\ x &= (A^TA)^{-1}A^Tb\\ 代入得p &= Ax=A(A^TA)^{-1}A^Tb \end{aligned} ATAxx代入得p=ATb=(ATA)−1ATb=Ax=A(ATA)−1ATb
这里的A(ATA)-1AT相当于投影到一维空间时的aaT/aTa,就是投影矩阵P
当 A 为可逆方阵时, P = A ( A T A ) − 1 A T = A A − 1 ( A T ) − 1 A T = I 因为 A 为 n × n 可逆方阵时,列空间为整个 n 维空间,把 n 维空间中的 b 投影到整个 n 维空间,投影矩阵为单位矩阵 当A为可逆方阵时,P=A(A^TA)^{-1}A^T=AA^{-1}(A^T)^{-1}A^T=I\\ 因为A为n\times n可逆方阵时,列空间为整个n维空间,把n维空间中的b投影到整个n维空间,投影矩阵为单位矩阵 当A为可逆方阵时,P=A(ATA)−1AT=AA−1(AT)−1AT=I因为A为n×n可逆方阵时,列空间为整个n维空间,把n维空间中的b投影到整个n维空间,投影矩阵为单位矩阵
投影矩阵的特性:
- PT=P
- P2=P:P2=A(ATA)-1**(ATA)(ATA)-1**AT=A(ATA)-1AT=P
应用:通过最小二乘法拟合一条直线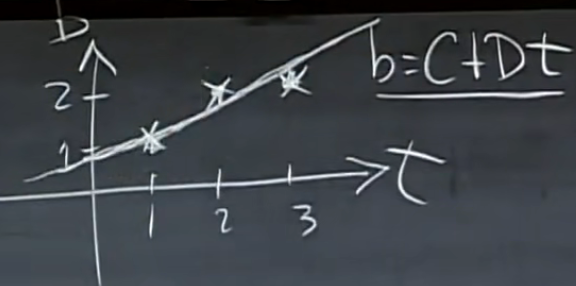
At=b无解,但是ATAt=ATb有解
投影矩阵和最小二乘
b一般会和平面有夹角,此时有垂直于平面和平行于平面的两个分量,平行的分量就是投影,投影矩阵就是把垂直的分量去除
若b在A的列空间里,Pb=b,即b在平面上
若b正交于A的列空间,Pb=0,即b垂直于平面

e也是一个投影,投影矩阵是(I-P),投影到了与P投影的空间相互正交的空间(这里是左零空间)
最小二乘:找拥有最小的各个误差的平方和的解
∥ e ∥ 2 = ∥ A x − b ∥ 2 最小二乘:使 e 1 2 + e 2 2 + e 3 2 最小的解 \|e\|^2=\|Ax-b\|^2\\ 最小二乘:使e^2_1+e^2_2+e^2_3最小的解 ∥e∥2=∥Ax−b∥2最小二乘:使e12+e22+e32最小的解
x = ( A T A ) − 1 A T b x=(A^TA)^{-1}A^Tb x=(ATA)−1ATb
线性回归分析:用误差的平方和作为测量总误差的标准
最小二乘法容易受到离群值的影响
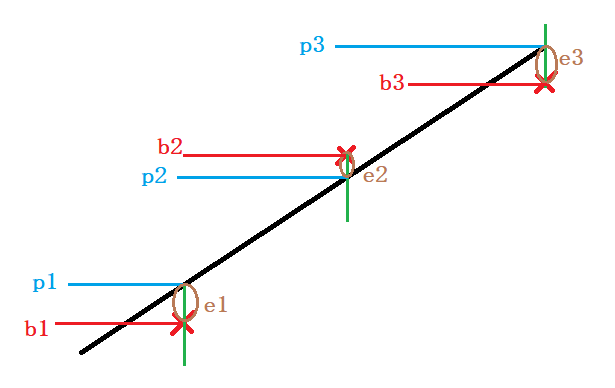
p+e=b
若矩阵A各列线性无关,则ATA可逆
证明:

互相垂直的各列一定线性无关(除零向量),这些互相垂直的列向量组成的向量组是标准正交的(标准正交向量组)
正交矩阵和Gram-Schmidt正交化
标准正交向量组中,向量相互正交,即转置相乘为0(内积),但与自身不正交,所以转置相乘为1:
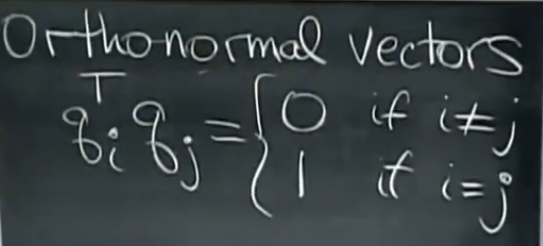
标准正交向量组组成的矩阵(标准正交矩阵):QTQ=I
当标准正交矩阵是方阵的时候(有逆矩阵)称为正交矩阵
Q T Q = I Q T = Q − 1 Q^TQ=I\\ Q^T=Q^{-1} QTQ=IQT=Q−1
当有一个方阵时,列互相正交、列向量的长度为1,那么就是正交矩阵:阿德玛矩阵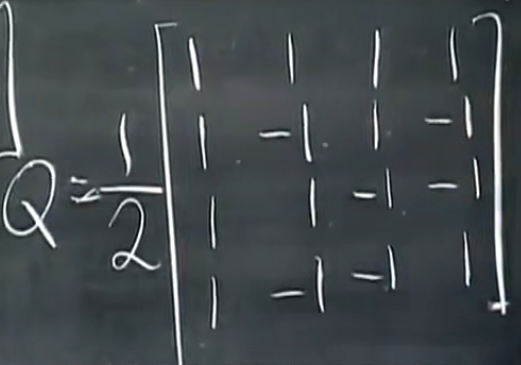
当投影到Q的列空间中:
P = Q ( Q T Q ) − 1 Q T = Q Q T 当 Q 是方阵时, P = Q Q T = I P=Q(Q^TQ)^{-1}Q^T=QQ^T\\ 当Q是方阵时,P=QQ^T=I P=Q(QTQ)−1QT=QQT当Q是方阵时,P=QQT=I
而对于拟合过程:
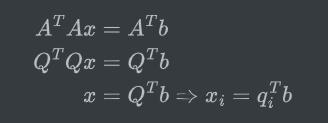
即已知标准正交基,则在第i个基方向上的投影就等于qiTb
格拉姆-施密特正交化:
从两个线性无关向量开始,取一个向量相对另一向量的垂直分量(e部分),获得一对相互正交的向量A和B,然后向量除长度从而标准化
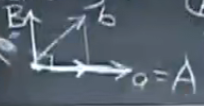
B = b − p = b − A T b A T A A 投影 p = a a T b a T a B=b-p=b-\frac{A^Tb}{A^TA}A\\ 投影p=a\frac{a^Tb}{a^Ta} B=b−p=b−ATAATbA投影p=aaTaaTb
证明:A⊥B
A T B = A T ( b − A T b A T A A ) = 0 A^TB=A^T(b-\frac{A^Tb}{A^TA}A)=0 ATB=AT(b−ATAATbA)=0
如果再有c要正交化:
C = c − p c 在 A 上的投影 − p c 在 B 上的投影 = c − A T c A T A A − B T c B T B B C=c-p_{c在A上的投影}-p_{c在B上的投影}=c-\frac{A^Tc}{A^TA}A-\frac{B^Tc}{B^TB}B C=c−pc在A上的投影−pc在B上的投影=c−ATAATcA−BTBBTcB
正交化后得到的向量组成的空间一样和原来线性无关的向量组成的列空间一样,但是正交化标准化后的Q=[q1 q2]比原来的[a b]要好
消元法矩阵表达式:A=LU
格拉姆-施密特法的矩阵表达式:
A = Q R [ a b ] = [ q 1 q 2 ] [ a T q 1 b T q 1 a T q 2 b T q 2 ] ( a T q 2 = 0 ) \begin{aligned} A&=QR\\ \begin{bmatrix} a & b \end{bmatrix} &= \begin{bmatrix} q_1 & q_2 \end{bmatrix} \begin{bmatrix} a^Tq_1 & b^Tq_1\\ a^Tq_2 & b^Tq_2 \end{bmatrix}\\ &(a^Tq_2=0) \end{aligned} A[a





 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 469
469

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








