knapsack problem 1049. Last Stone Weight II 494. Target Sum 474. Ones and Zeroes

1049. Last Stone Weight II

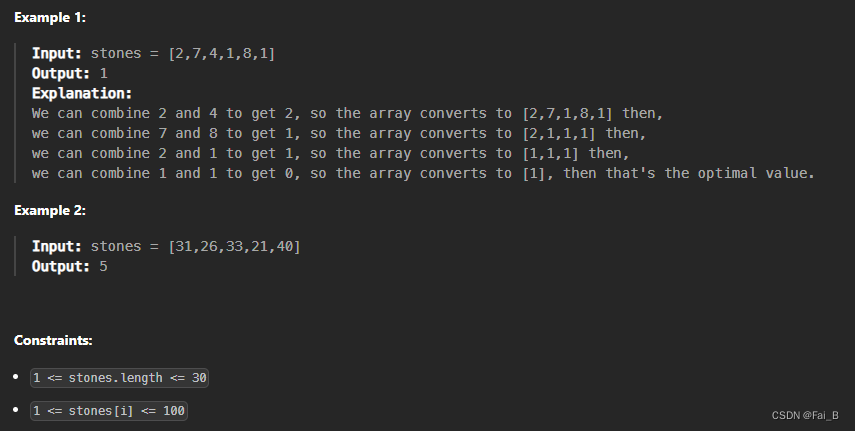
You are given an array of integers stones where stones[i] is the weight of the ith stone.

We are playing a game with the stones. On each turn, we choose any two stones and smash them together. Suppose the stones have weights x and y with x <= y. The result of this smash is:

• If x == y, both stones are destroyed, and
• If x != y, the stone of weight x is destroyed, and the stone of weight y has new weight y - x.

At the end of the game, there is at most one stone left.

Return the smallest possible weight of the left stone. If there are no stones left, return 0.

 

1. find a backpack ,it has a upper limit of half the total weight of all stones

2. Find the maximum weight that can load in this backpack

3.Because it's rounding up to 0, this backpack can only hold less than or equal to half of the total weight

4.so after smashes,  we can get the last remain weight by : half maximum weight - maximum backpack weight - maximum backpack weight

1-dimensional DP：

Time complexity: O(m × n) ：  m is the total weight of the stone (half of the total weight), n is the number of stones
Space complexity: O(m)

class Solution:
    def lastStoneWeightII(self, stones):
        total_sum = sum(stones)
        target = total_sum // 2
        dp = [0] * (target + 1)
        for stone in stones:
            for j in range(target, stone - 1, -1):
                dp[j] = max(dp[j], dp[j - stone] + stone)
        return total_sum - 2* dp[-1]

2-dimensional DP：

class Solution:
    def lastStoneWeightII(self, stones: List[int]) -> int:
        total_sum = sum(stones)
        target = total_sum // 2
        
        # 创建二维dp数组，行数为石头的数量加1，列数为target加1
        # dp[i][j]表示前i个石头能否组成总重量为j
        dp = [[False] * (target + 1) for _ in range(len(stones) + 1)]
        
        # 初始化第一列，表示总重量为0时，前i个石头都能组成
        for i in range(len(stones) + 1):
            dp[i][0] = True
        
        for i in range(1, len(stones) + 1):
            for j in range(1, target + 1):
                # 如果当前石头重量大于当前目标重量j，则无法选择该石头
                if stones[i - 1] > j:
                    dp[i][j] = dp[i - 1][j]
                else:
                    # 可选择该石头或不选择该石头
                    dp[i][j] = dp[i - 1][j] or dp[i - 1][j - stones[i - 1]]
        
        # 找到最大的重量i，使得dp[len(stones)][i]为True
        # 返回总重量减去两倍的最接近总重量一半的重量
        for i in range(target, -1, -1):
            if dp[len(stones)][i]:
                return total_sum - 2 * i
        
        return 0

 

494. Target Sum

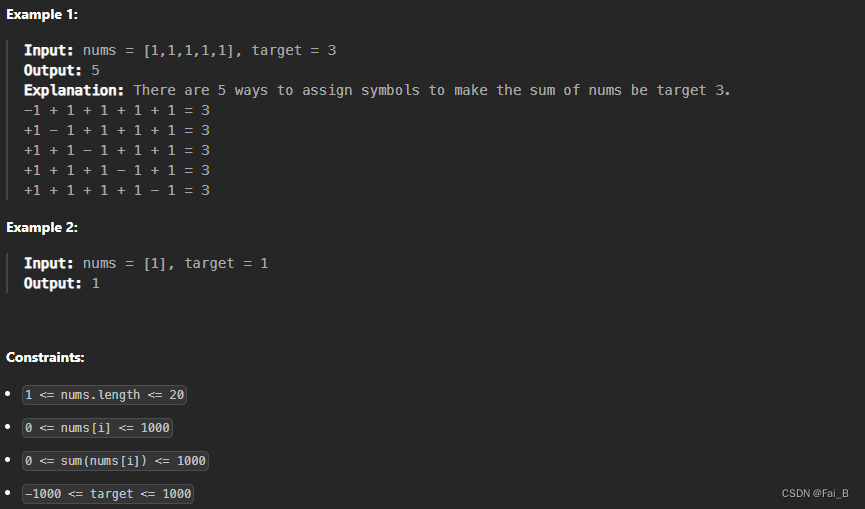
You are given an integer array nums and an integer target.

You want to build an expression out of nums by adding one of the symbols '+' and '-' before each integer in nums and then concatenate all the integers.

• For example, if nums = [2, 1], you can add a '+' before 2 and a '-' before 1 and concatenate them to build the expression "+2-1".

Return the number of different expressions that you can build, which evaluates to target.

 

1. Since it is a target, there must be a left combination - right combination = target.

2. left + right = sum, and sum is fixed. right = sum - left

3. Here's the formula: left - (sum - left) = target Derived from left = (target + sum)/2 .

4. target is fixed, sum is fixed, left can be found.

5. At this point, the problem is to find the combination/subsets of left_sum in the set of nums.

so the problem become: How many ways are there to fill a knapsack with a capacity of (target + sum) / 2?

(6. If target+sum is odd, there is no expression that can make this work)

1-dimensional DP:

Time complexity: O(n × m), n is the number of positive numbers, m is the knapsack capacity
Space complexity: O(m), m is the knapsack capacity

class Solution:
    def findTargetSumWays(self, nums: List[int], target: int) -> int:
        total_sum = sum(nums)  # 计算nums的总和
        if abs(target) > total_sum:
            return 0  # 此时没有方案
        if (target + total_sum) % 2 == 1:
            return 0  # 此时没有方案
        target_sum = (target + total_sum) // 2  # 目标和
        dp = [0] * (target_sum + 1)  # 创建动态规划数组，初始化为0
        dp[0] = 1  # 当目标和为0时，只有一种方案，即什么都不选
        for num in nums:
            for j in range(target_sum, num - 1, -1):
                dp[j] += dp[j - num]  # 状态转移方程，累加不同选择方式的数量
        return dp[target_sum]  # 返回达到目标和的方案数

2-dimensional DP:

class Solution:
    def findTargetSumWays(self, nums: List[int], target: int) -> int:
        total_sum = sum(nums)  # 计算nums的总和
        if abs(target) > total_sum:
            return 0  # 此时没有方案
        if (target + total_sum) % 2 == 1:
            return 0  # 此时没有方案
        target_sum = (target + total_sum) // 2  # 目标和

        # 创建二维动态规划数组，行表示选取的元素数量，列表示累加和
        dp = [[0] * (target_sum + 1) for _ in range(len(nums) + 1)]

        # 初始化状态
        dp[0][0] = 1

        # 动态规划过程
        for i in range(1, len(nums) + 1):
            for j in range(target_sum + 1):
                dp[i][j] = dp[i - 1][j]  # 不选取当前元素
                if j >= nums[i - 1]:
                    dp[i][j] += dp[i - 1][j - nums[i - 1]]  # 选取当前元素

        return dp[len(nums)][target_sum]  # 返回达到目标和的方案数

 backtracking:

class Solution:


    def backtracking(self, candidates, target, total, startIndex, path, result):
        if total == target:
            result.append(path[:])  # 将当前路径的副本添加到结果中
        # 如果 sum + candidates[i] > target，则停止遍历
        for i in range(startIndex, len(candidates)):
            if total + candidates[i] > target:
                break
            total += candidates[i]
            path.append(candidates[i])
            self.backtracking(candidates, target, total, i + 1, path, result)
            total -= candidates[i]
            path.pop()

    def findTargetSumWays(self, nums: List[int], target: int) -> int:
        total = sum(nums)
        if target > total:
            return 0  # 此时没有方案
        if (target + total) % 2 != 0:
            return 0  # 此时没有方案，两个整数相加时要注意数值溢出的问题
        bagSize = (target + total) // 2  # 转化为组合总和问题，bagSize就是目标和

        # 以下是回溯法代码
        result = []
        nums.sort()  # 需要对nums进行排序
        self.backtracking(nums, bagSize, 0, 0, [], result)
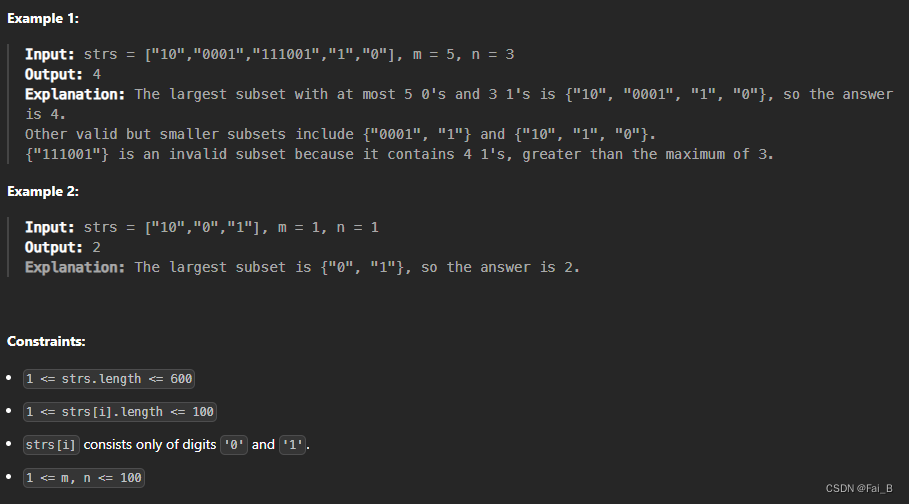
        return len(result)

474. Ones and Zeroes

You are given an array of binary strings strs and two integers m and n.

Return the size of the largest subset of strs such that there are at most m 0's and n 1's in the subset.

A set x is a subset of a set y if all elements of x are also elements of y.

 

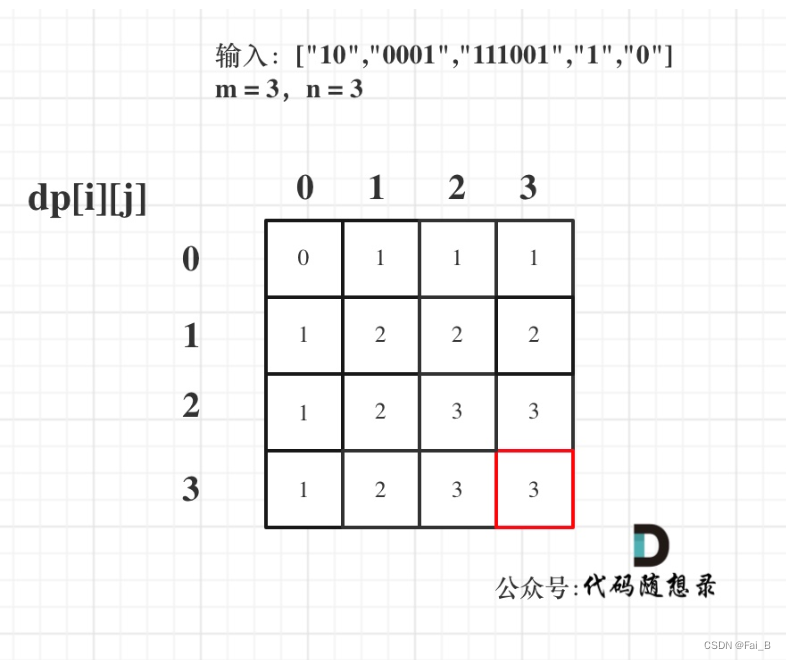
1.dp[i][j]: the size of the largest subset of strs with at most i zeros and j ones is dp[i][j]. m and n are the two dimensions of the knapsack

2.Recurrence formula: dp[i][j] = max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1)

 

Time complexity: O(kmn),   k is the length of strs
Space complexity: O(mn)

class Solution:
    def findMaxForm(self, strs: List[str], m: int, n: int) -> int:
        dp = [[0] * (n + 1) for _ in range(m + 1)]  # 创建二维动态规划数组，初始化为0
        for s in strs:  # 遍历物品
            zeroNum = s.count('0')  # 统计0的个数
            oneNum = len(s) - zeroNum  # 统计1的个数
            #if zeroNum > m or oneNum > n:
            #    continue
            for i in range(m, zeroNum - 1, -1):  # 遍历背包容量且从后向前遍历
                for j in range(n, oneNum - 1, -1):
                    dp[i][j] = max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1)  # 状态转移方程
        return dp[m][n]

m,n 是这个背包的两个维度，不是两个物品所以还是 01背包问题