518. Coin Change II 377. Combination Sum IV

最新推荐文章于 2024-03-28 22:02:50 发布

原创最新推荐文章于 2024-03-28 22:02:50 发布 · 544 阅读

8 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #leetcode #职场和发展

本文介绍了如何用动态规划解决CoinChangeII的硬币组合问题及CombinationSumIV的整数组合计数，涉及无限数量物品和组合顺序的考虑。

518. Coin Change II

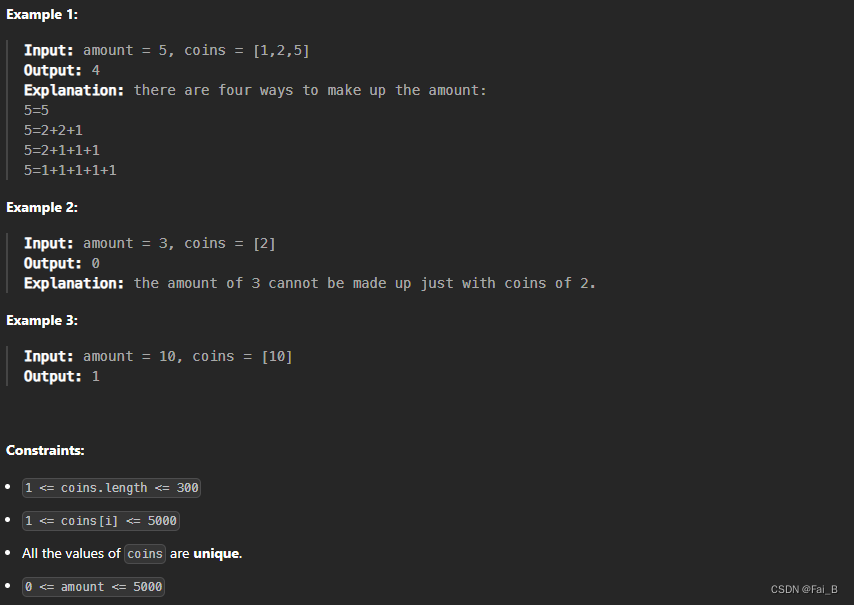
You are given an integer array coins representing coins of different denominations and an integer amount representing a total amount of money.

Return the number of combinations that make up that amount. If that amount of money cannot be made up by any combination of the coins, return 0.

You may assume that you have an infinite number of each kind of coin.

The answer is guaranteed to fit into a signed 32-bit integer.

Like the knapsack problem, but there are unlimited number of each item!

so Change the traversal order can be done!

AC:

Time complexity: O(m x n) m is the size of knapsack, n is the size of soins

Space complexity: O(m)

class Solution:
    def change(self, amount: int, coins: List[int]) -> int:

        dp = [0] * (amount + 1)
        dp[0] = 1

        for coin in coins:
            for j in range(coin, amount + 1):
                dp[j] += dp[j - coin]
        
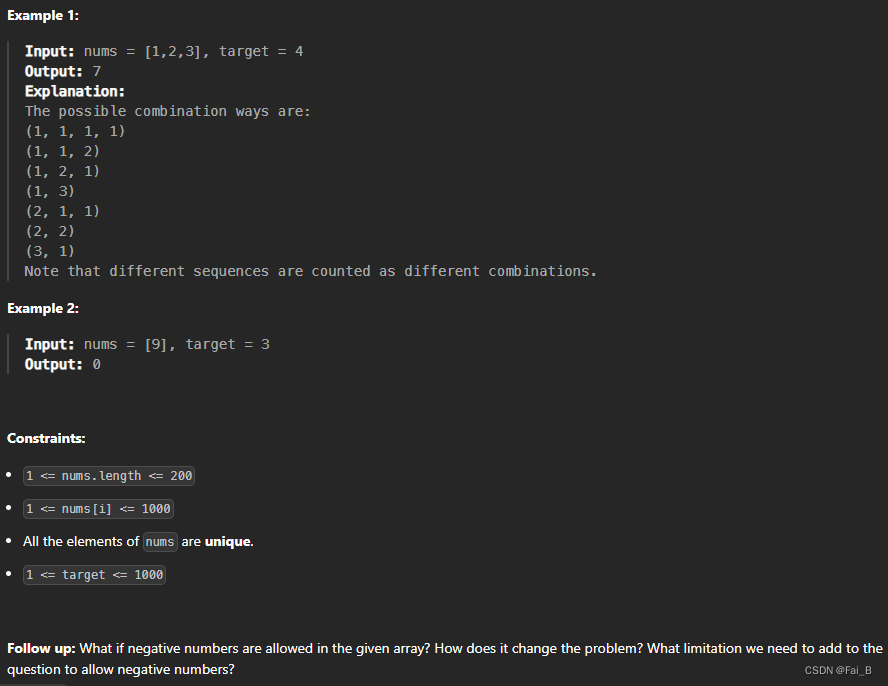
        return dp[-1]

377. Combination Sum IV

Given an array of distinct integers nums and a target integer target, return the number of possible combinations that add up to target.

The test cases are generated so that the answer can fit in a 32-bit integer.

Combinations in a different order also count!!!!! : Different ways to load a backpack

Traverse the knapsack first, then the items. ( if i > num : continue traverse)

class Solution:
    def combinationSum4(self, nums: List[int], target: int) -> int:
        dp = [0] * (target + 1)  # 创建动态规划数组，用于存储组合总数
        dp[0] = 1  # 初始化背包容量为0时的组合总数为1

        for i in range(1, target + 1):  # 遍历背包容量
            for j in nums:  # 遍历物品列表
                if i >= j:  # 当背包容量大于等于当前物品重量时
                    dp[i] += dp[i - j]  # 更新组合总数

        return dp[-1]  # 返回背包容量为target时的组合总数