💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文内容如下:🎁🎁🎁
⛳️赠与读者
👨💻做科研,涉及到一个深在的思想系统,需要科研者逻辑缜密,踏实认真,但是不能只是努力,很多时候借力比努力更重要,然后还要有仰望星空的创新点和启发点。建议读者按目录次序逐一浏览,免得骤然跌入幽暗的迷宫找不到来时的路,它不足为你揭示全部问题的答案,但若能解答你胸中升起的一朵朵疑云,也未尝不会酿成晚霞斑斓的别一番景致,万一它给你带来了一场精神世界的苦雨,那就借机洗刷一下原来存放在那儿的“躺平”上的尘埃吧。
或许,雨过云收,神驰的天地更清朗.......🔎🔎🔎
💥1 概述
复现文献:

随着高比例可再生能源接入电网,电力系统灵活性不足的问题日益凸显。可再生能源与可控分布式资源可通过虚拟电厂进行聚合管理,在一定程度上缓解对灵活性的需求。尽管新建储能系统可弥补灵活性缺口,但其初始投资成本高昂。为此,本文提出一种基于碳配额与价格联动的燃煤机组租赁机制,向虚拟电厂出让燃煤机组使用权。随后,利用不同需求响应策略调控多类用户的可控负荷,为虚拟电厂提供可控资源。此外,为保证虚拟电厂运营商实现最优决策,采用能够精确刻画储能系统容量衰减状态的成本模型。进而实施虚拟电厂多时间尺度调度策略,充分利用不同时间尺度的可控资源,有效应对多重不确定性导致的功率失衡。结果表明,利用燃煤机组租赁机制并采用多用户需求响应策略,可为虚拟电厂提供灵活性;运营商所用容量衰减模型的精度对调度方案的最优性具有显著影响。
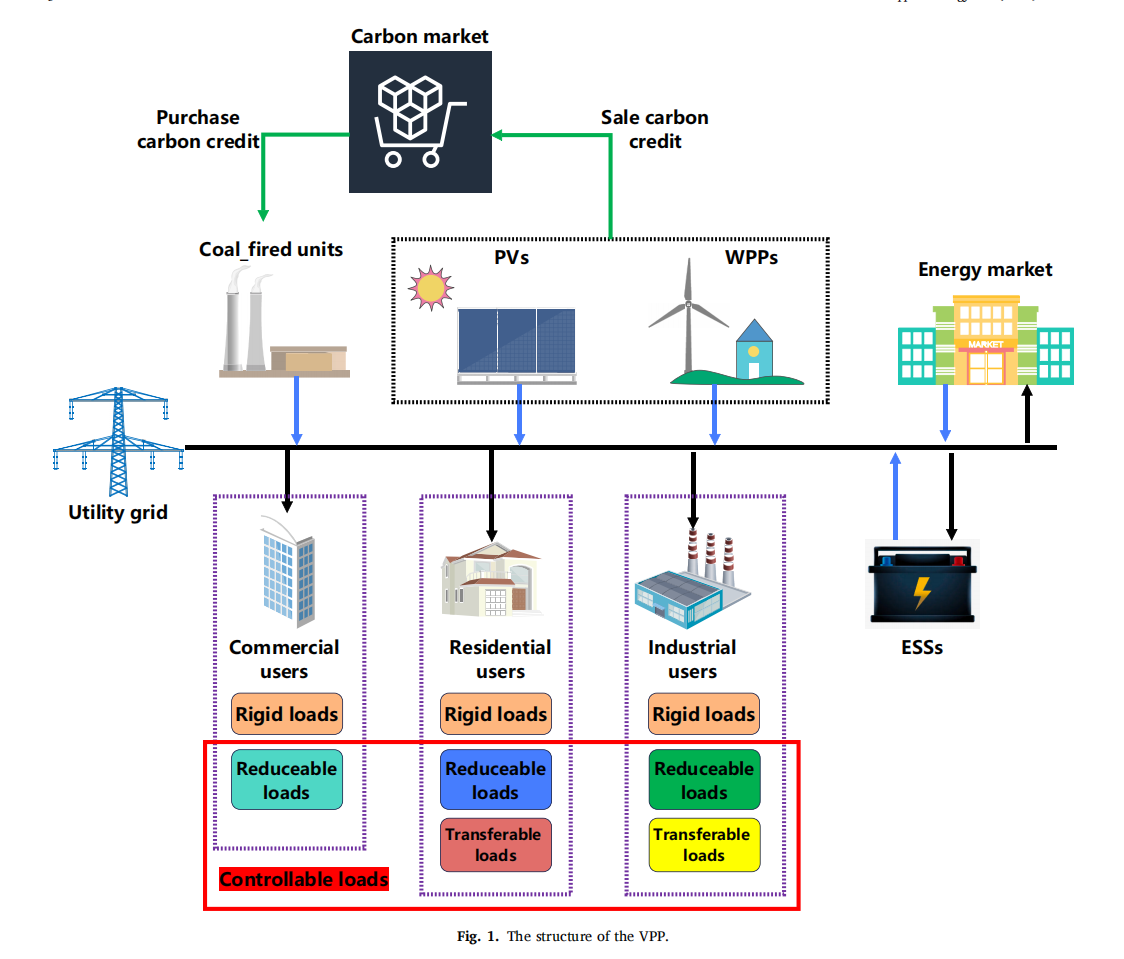
能源短缺、污染与气候变化已成全球“紧箍咒”。要同时满足高效、低碳、安全、可靠四大目标,传统“烧化石”模式必须退场,风光等可再生能源被寄予厚望。但风光“看天吃饭”,大规模并网后,电网随时面临“过山车”式波动;新建储能可平抑波动,却贵得惊人,再加上电价、负荷双重不确定,系统运行犹如“蒙眼走钢丝”。虚拟电厂(VPP)应运而生——它把分散在角落的光伏、储能、可控负荷、电动车“串珠成链”,以“云电厂”身份参与市场。然而,要让这条“链”坚韧耐摔,还得解开三道紧箍:随机性怎么量化?储能老化如何精准画像?用户弹性怎样按需激活?
学界已把VPP调度“翻过来研究”,但三大痛点仍像“暗礁”:
-
不确定处理:场景法一多就“算不动”,一少就“失真”;鲁棒优化太“保守”,钱包先喊疼;概率期望看似优雅,真实分布却常“打脸”;AI预测短时准、长时飘,计划永远“慢半拍”。
-
需求响应:工业、商业、居民用电习性“天壤之别”,过去“一刀切”的电价或补贴,往往“大棒打棉花”,弹性白白流失。
-
储能老化:循环一次老一次,DOD、SOC 把寿命“往死里卷”。若调度漠视老化,计划与实物“两张皮”,投运三年就“力不从心”。
本文把“暗礁”一一敲掉,给出四维“工具包”:
工具一:煤电租赁+碳信用——“借锅做饭”
不再重资产新建储能,而是短期租赁煤电机组调节能力,租金用“碳信用”结算:多排多付、少排少付。煤电获得“第二春”,VPP 手握“灵活外挂”,零土建、零长贷,就能给可再生能源“加缓冲垫”。
工具二:ISBDR 精准响应——“一户一策”
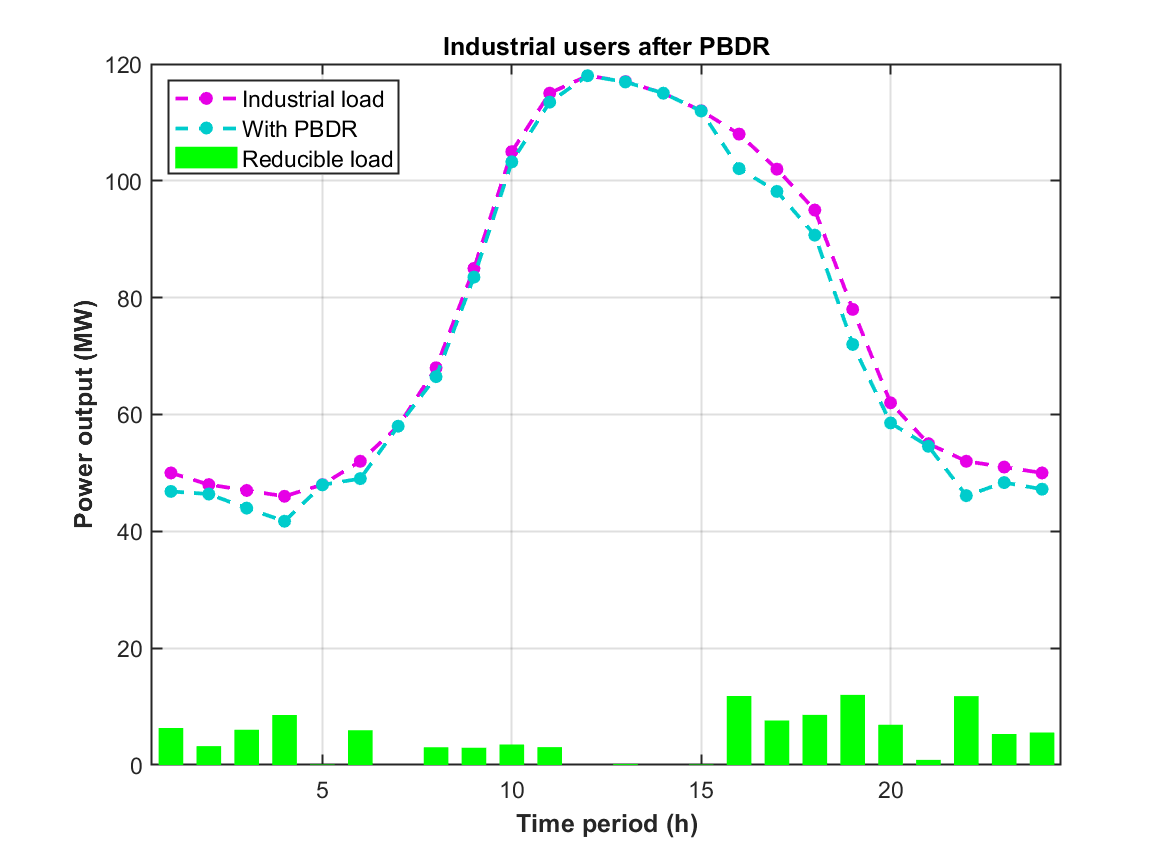
把用户切成工业、商业、居民三条“弹性曲线”:工业连续生产,给“中断高价”;商业时段集中,推“错峰折扣”;居民弹性最大,玩“游戏化补贴”。让每一度可削减负荷都“长在”用户舒适区,DR 参与率与资源利用率双升。
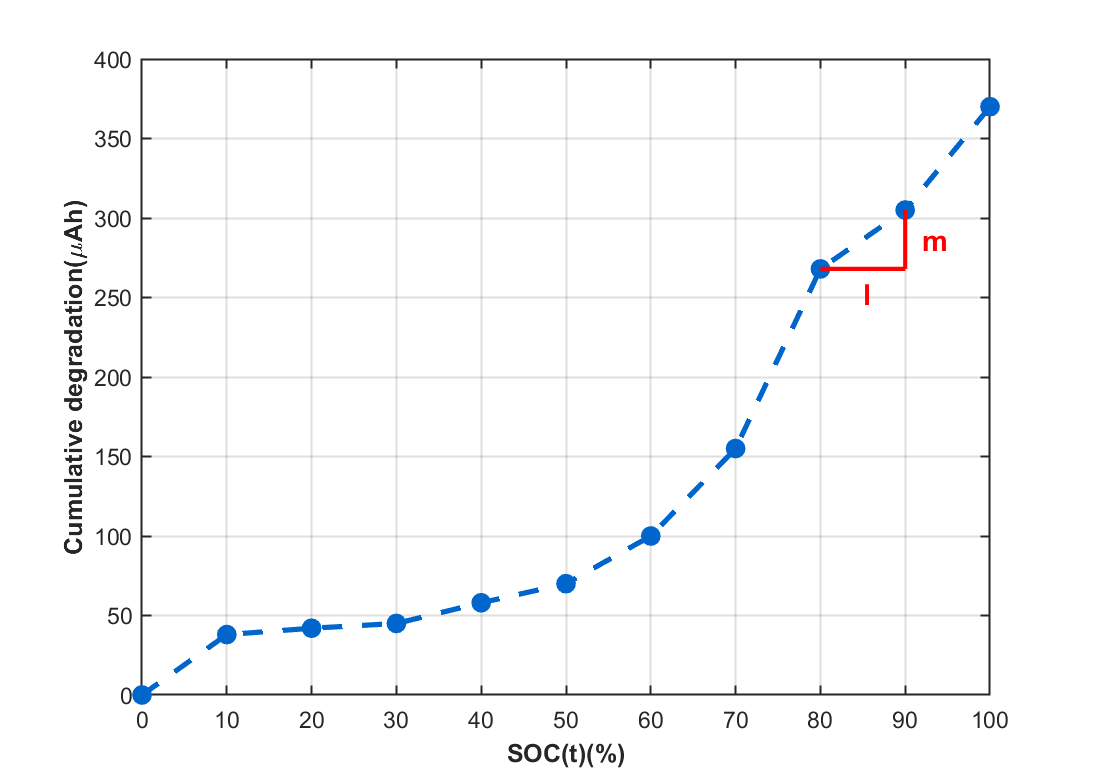
工具三:DOD-SOC 老化模型——“寿命仪表盘”
把循环深度、荷电状态嵌进调度目标函数,实时反馈“剩余循环次数”。调度员一眼看出“多充一次=少活三天”,计划从“盲开”变“精驾”,储能寿命延长,全生命周期成本直降。
工具四:多时间尺度滚动——“导航实时纠偏”
日前计划画“大路线”,小时内预测当“高德实时路况”,滚动修正。既防“长预测跑偏”,又避“短预测碎尸”,四重不确定(风光、负荷、电价)被层层稀释,调度鲁棒性肉眼可见地提升。
算例结果显示:组合拳打下去,VPP 运行成本下降、储能利用率提高、市场收益增加,煤电也在碳价倒逼下“越灵活越赚钱”。这套“租赁-响应-老化-滚动”四维方案,把“高比例可再生能源”最头疼的灵活性缺口,拆成四段可落地路径,对运营商、科研人员、政策制定者都是“拿来即用”的工具箱。能源转型进入深水区,VPP 要真正挑大梁,这篇论文值得学习收藏。
结论与展望
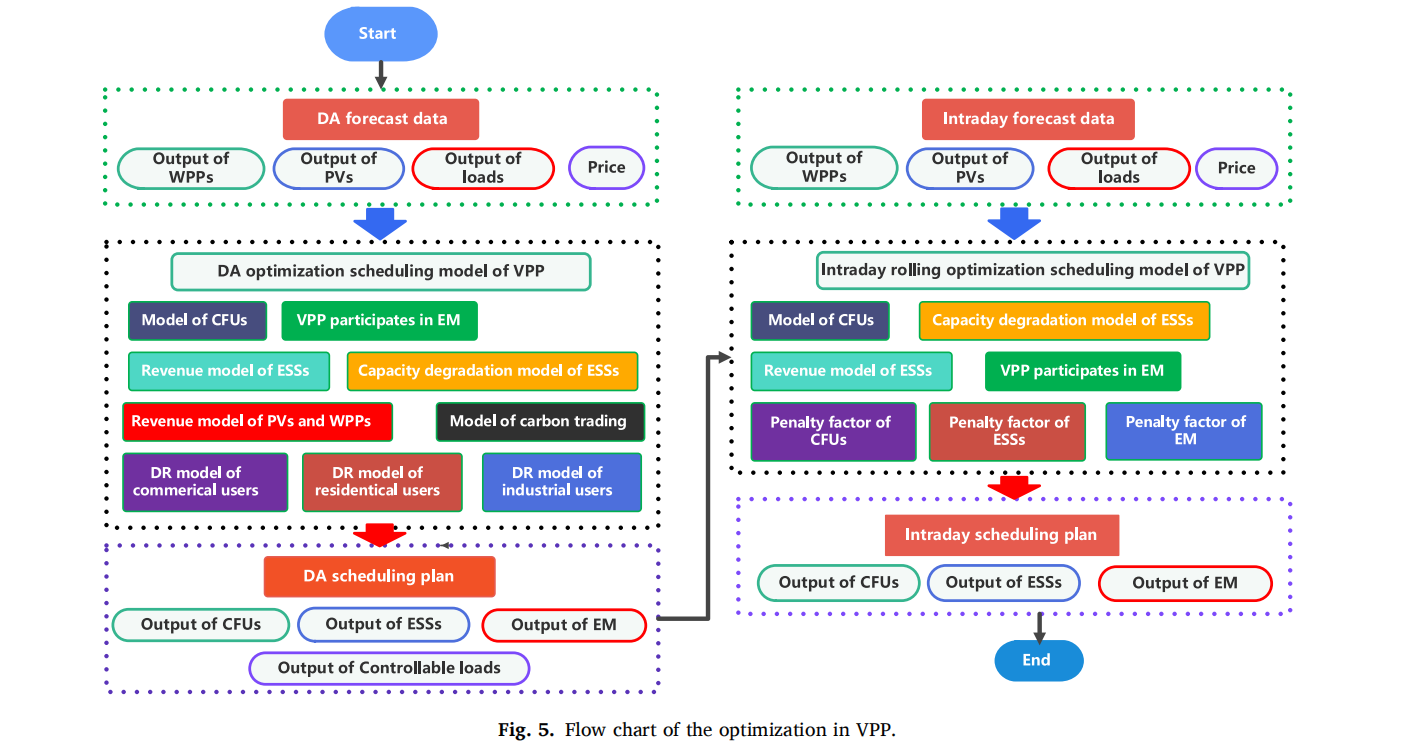
本研究提出了一种基于燃煤机组(CFU)使用权租赁机制与多用户需求响应(DR)策略的虚拟电厂(VPP)多时间尺度经济调度策略。为保护储能系统(ESS)利益并确保VPP运营商制定最优调度方案,本文采用同时考虑放电深度(DOD)与荷电状态(SOC)的ESS容量衰减模型。策略分为日前(DA)与日内两个时间尺度。数值分析得出以下主要结论:
1. 基于电价与碳配额联动的CFU使用权租赁机制,可为电力系统提供一定灵活性,并延缓CFU退役,避免资源浪费;该机制适用于短期内可控资源不足的场景。
2. 与经典衰减模型相比,新容量衰减模型使各ESS利用率分别下降30.58%、26.69%与8.19%;若运营商改用两种典型旧模型,VPP运行成本将分别上升7.09%与1.87%。可见,衰减模型能否准确描述ESS退化状态,不仅关乎VPP调度决策的最优性,也影响内部成员后续收益分配。
3. VPP运营商对商业与居民用户采用阶梯型激励DR(SIBDR)策略,对工业用户采用激励型DR(IBDR)与价格型DR(PBDR)策略,不仅使VPP在电力市场(EM)中的互动成本降低27.2%,还令其总成本下降3.8%。此外,依据不同用户负荷特性定制DR策略,可提升各方参与积极性。
4. VPP多时间尺度协调调度策略能充分利用不同时段的可控资源,有效应对风电、光伏、负荷及电价四类不确定性导致的功率失衡。
然而,本文仍存在不足:ESS模型需借助更多实验数据进一步细化;用户DR的可调度潜力尚需基于用能特征与数据加以量化。这些问题将在未来工作中继续深入研究。
📚2 运行结果
2.1 数据及基础求解结果

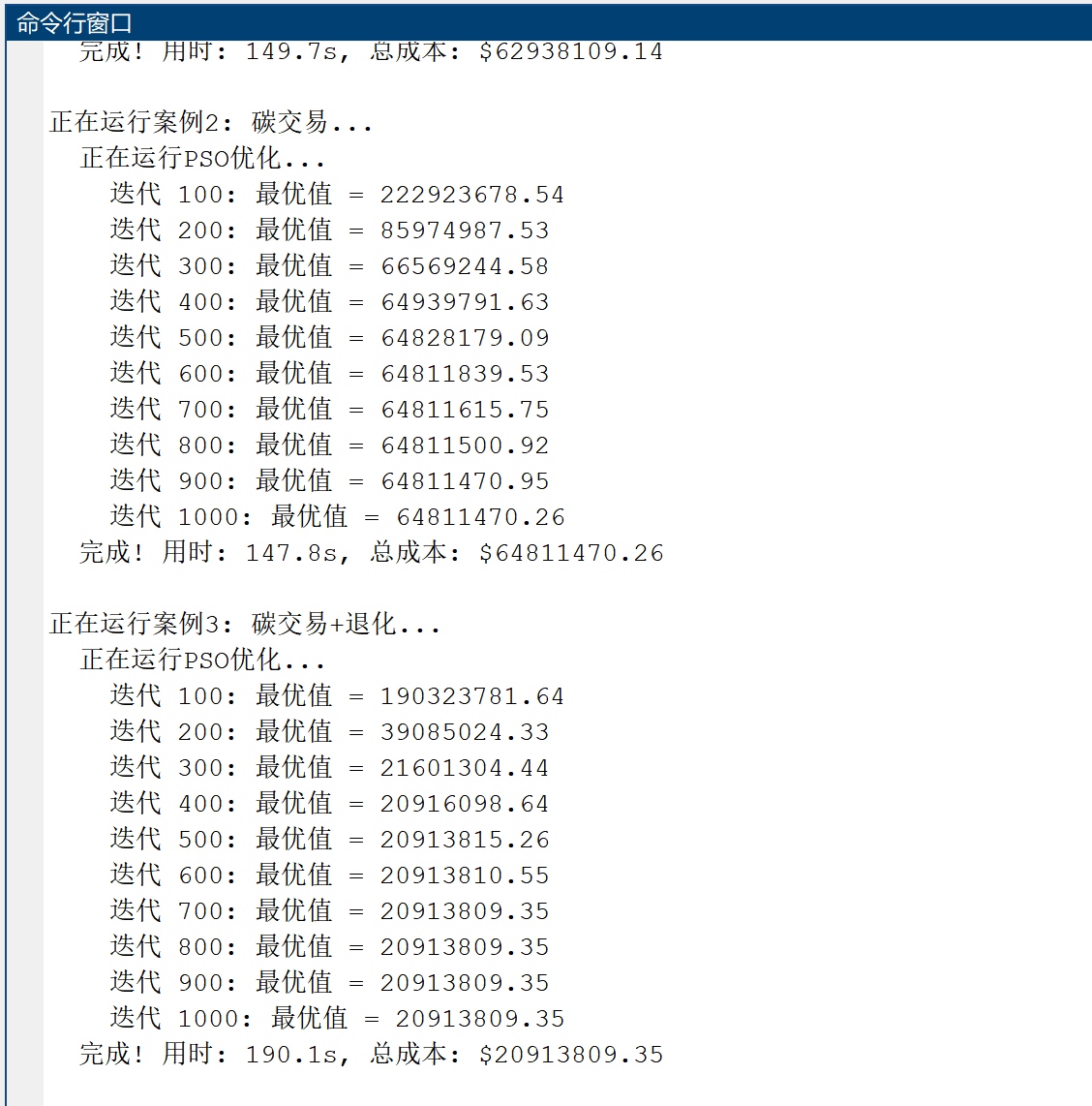
2.2 碳交易、碳交易+退化求解结果
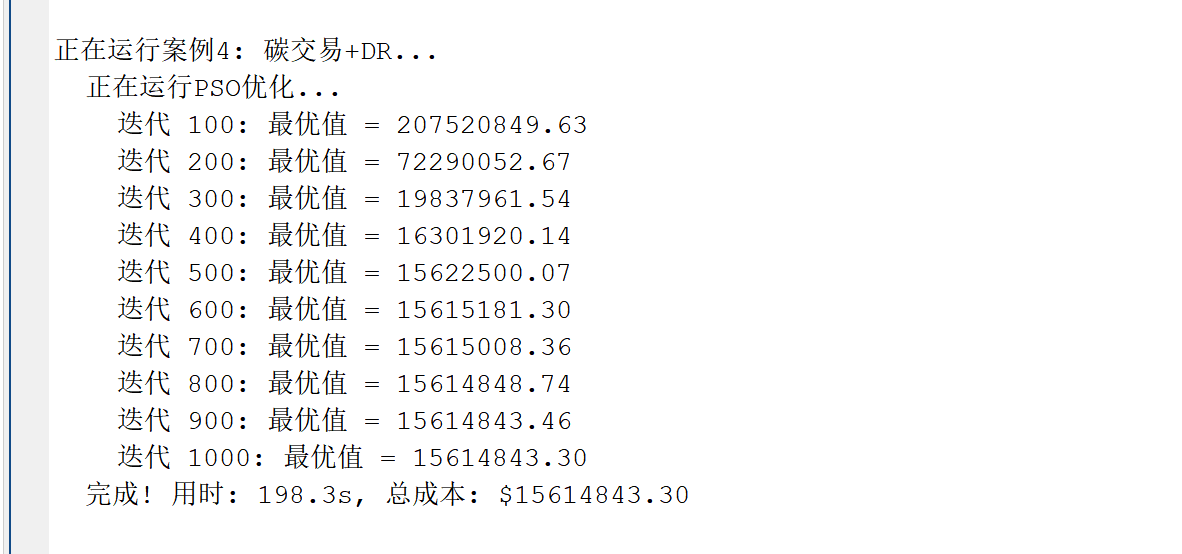
2.3 碳交易+DR求解结果
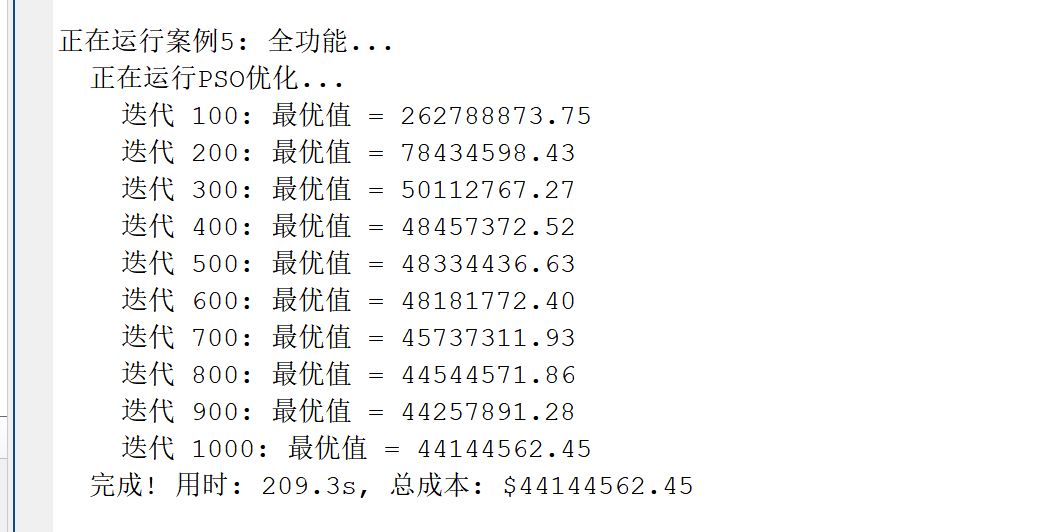
2.4 全功能求解
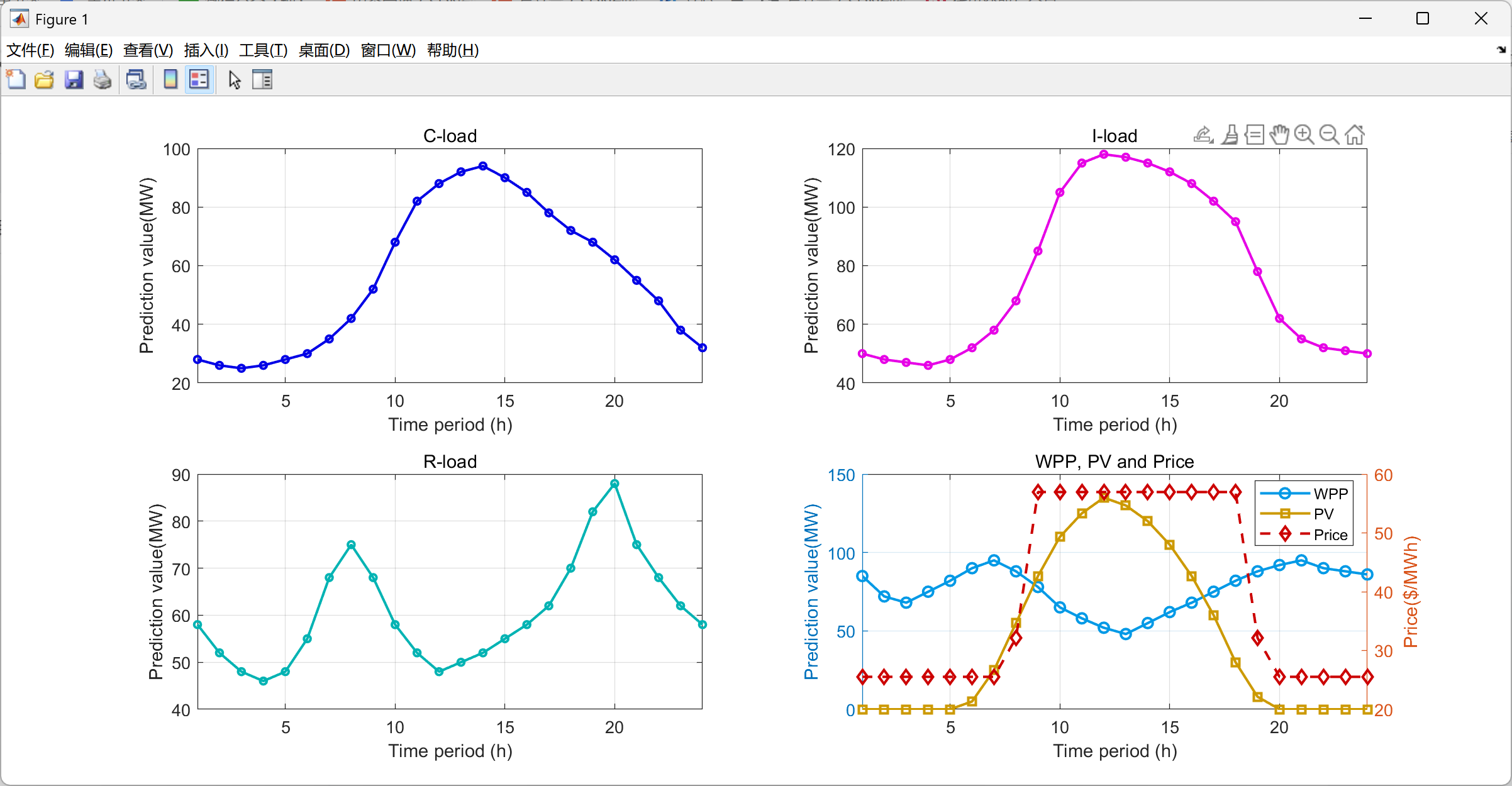
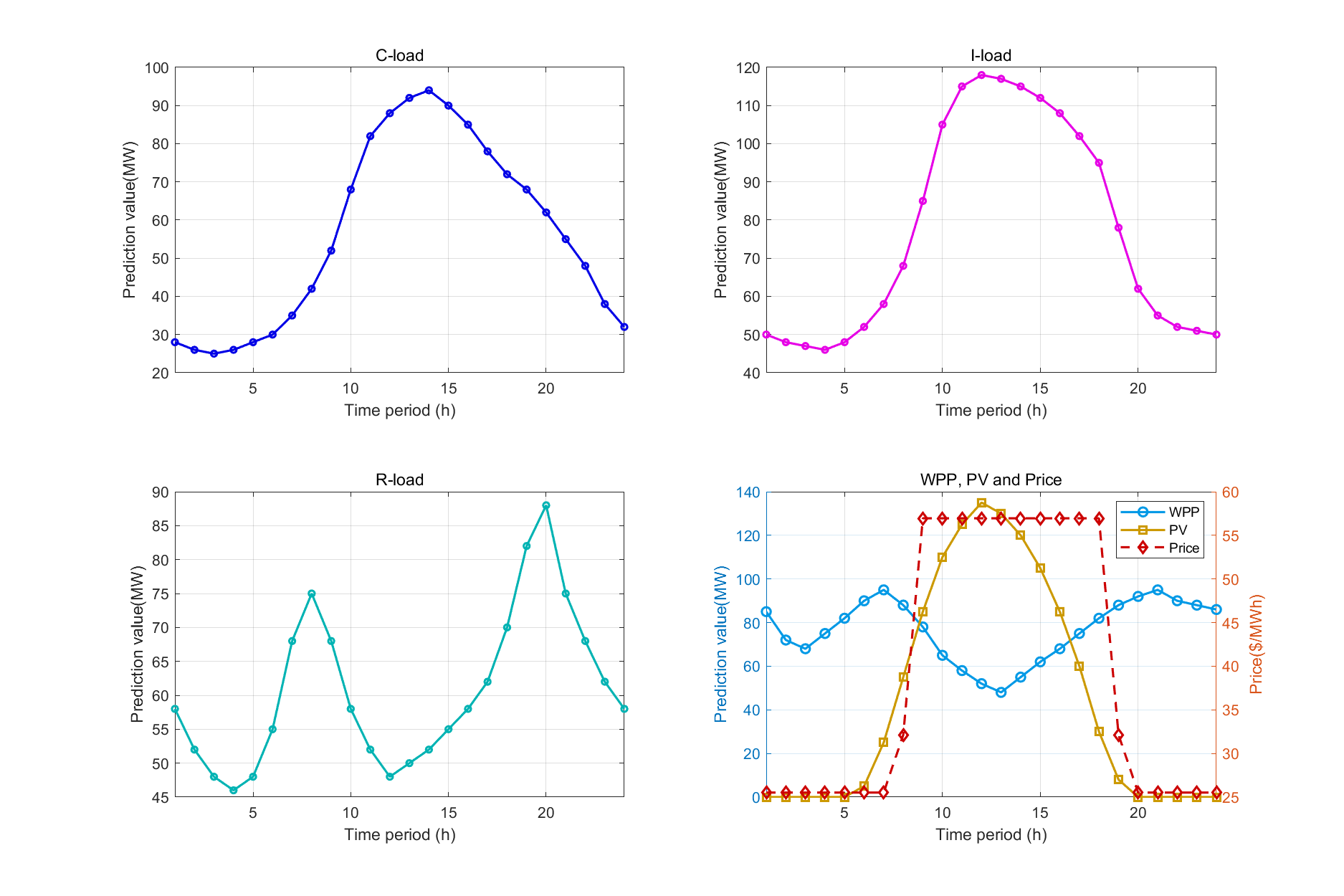
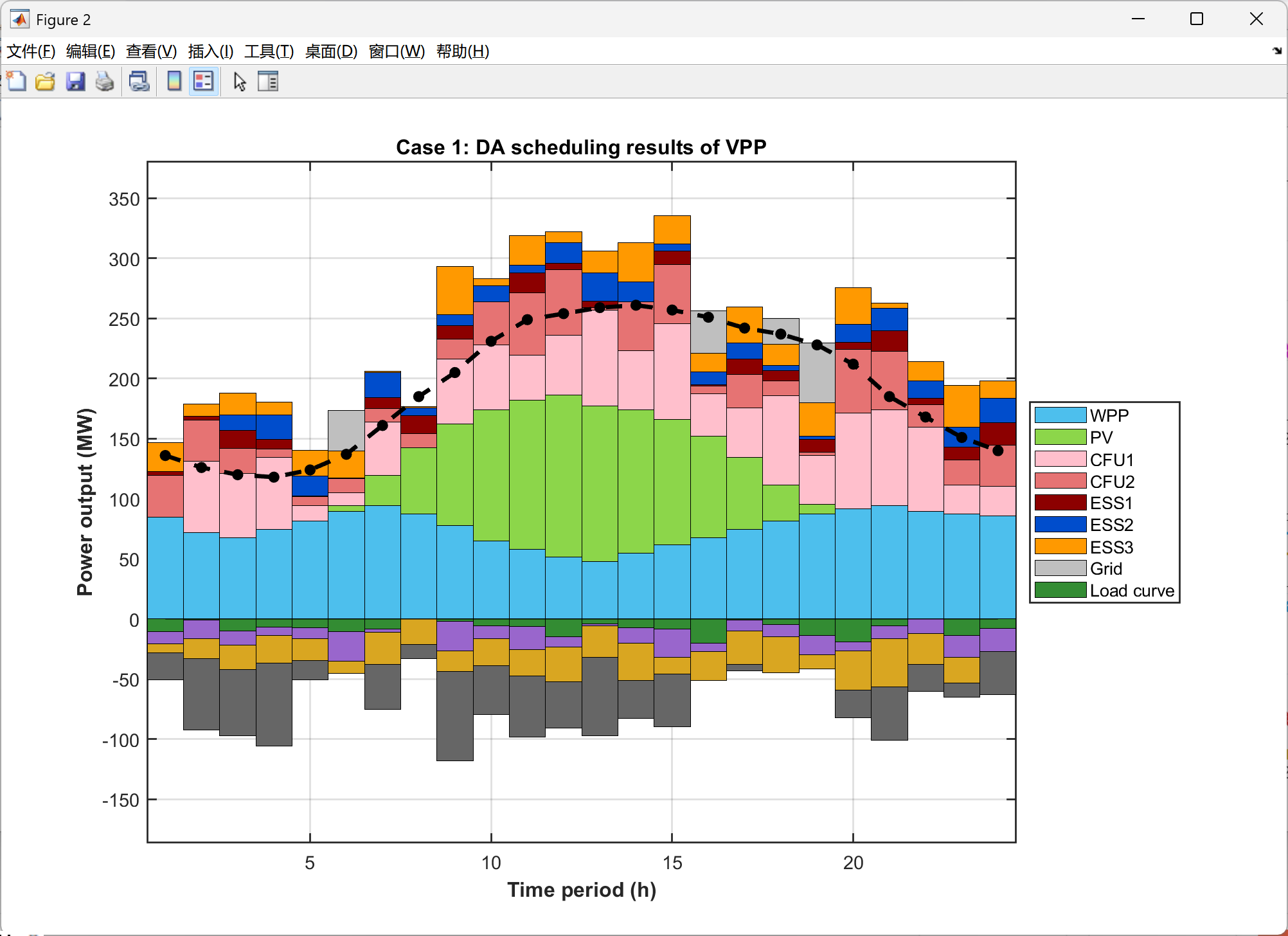
2.5 可视化结果展示

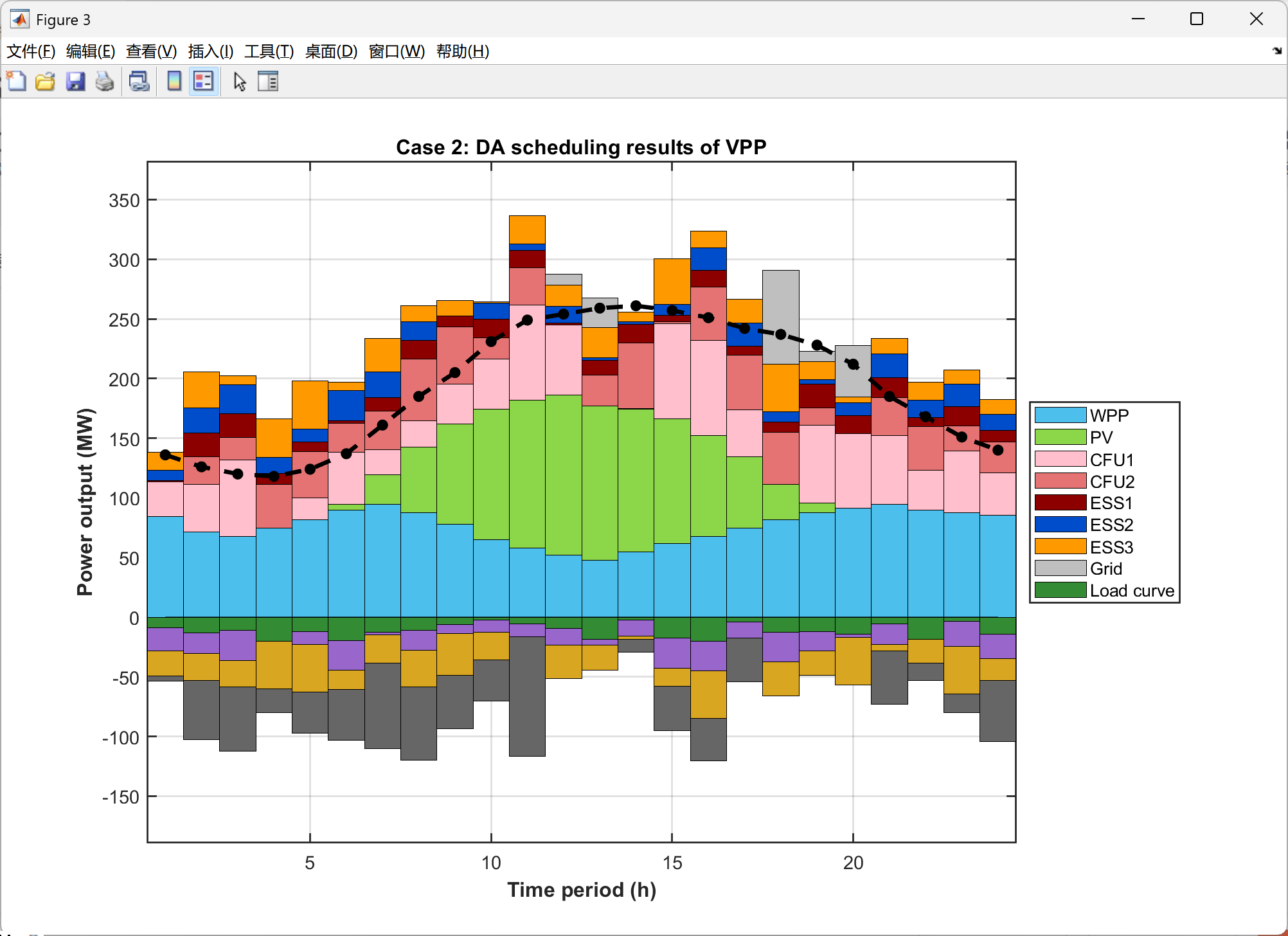
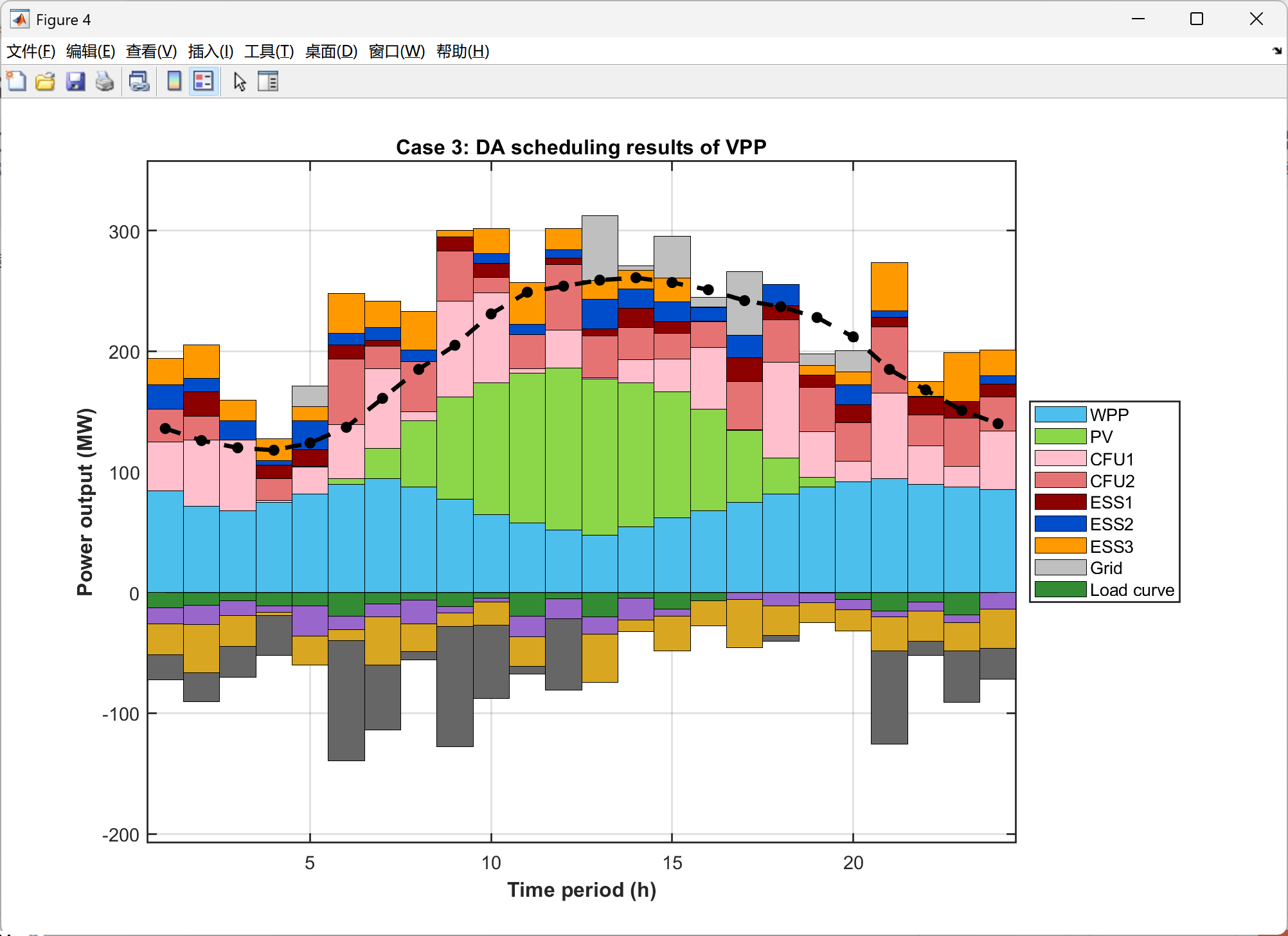
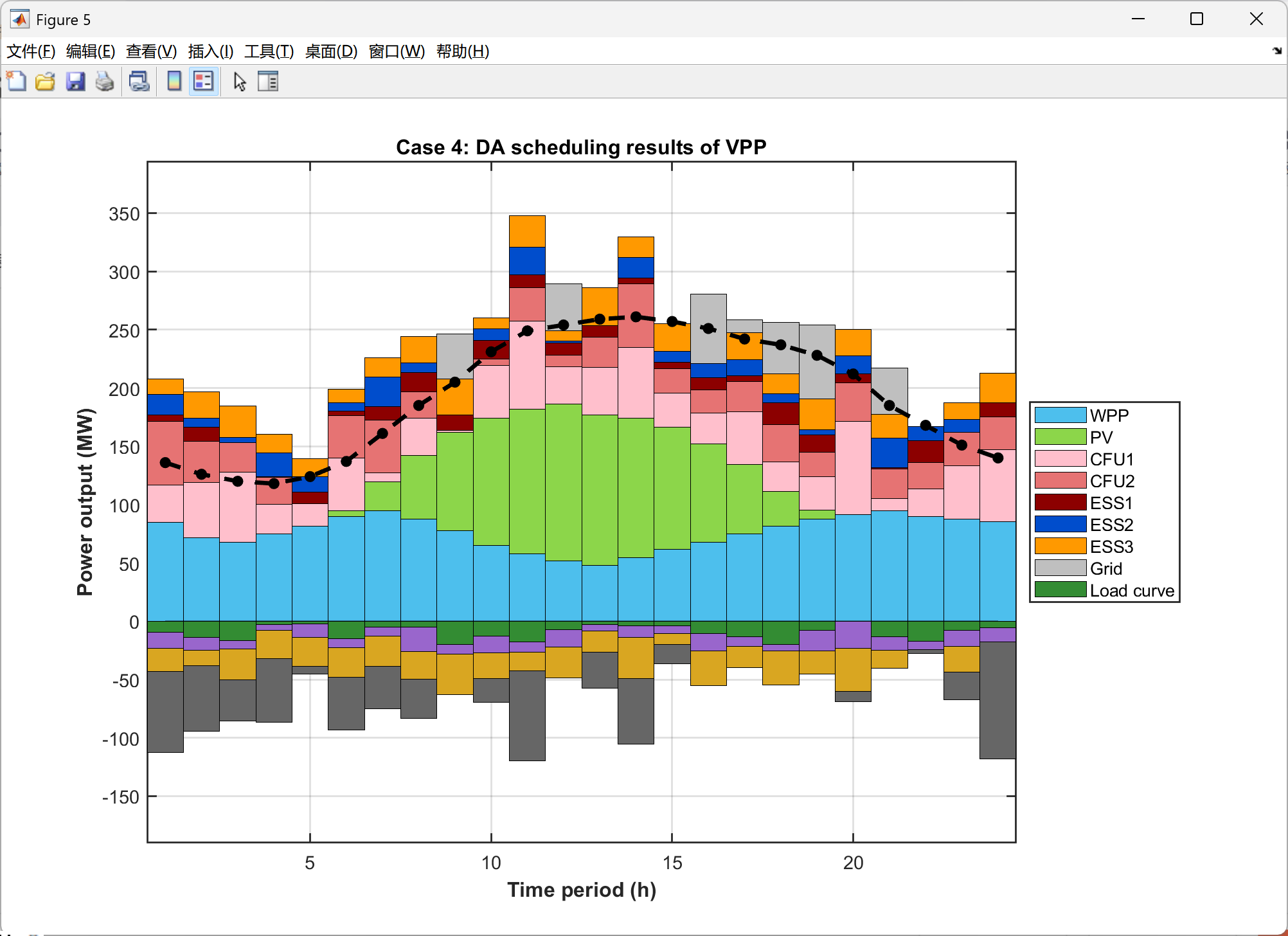
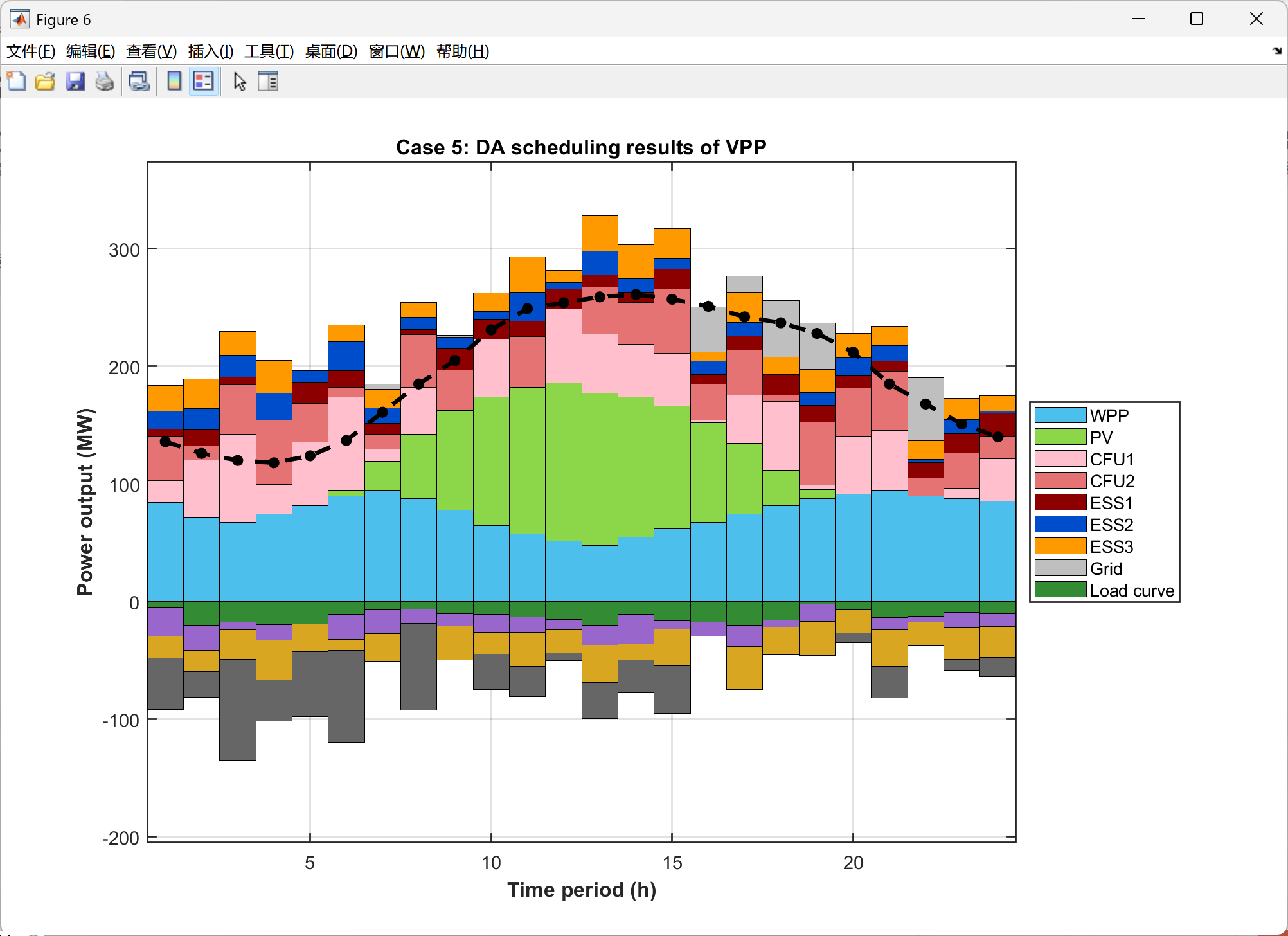
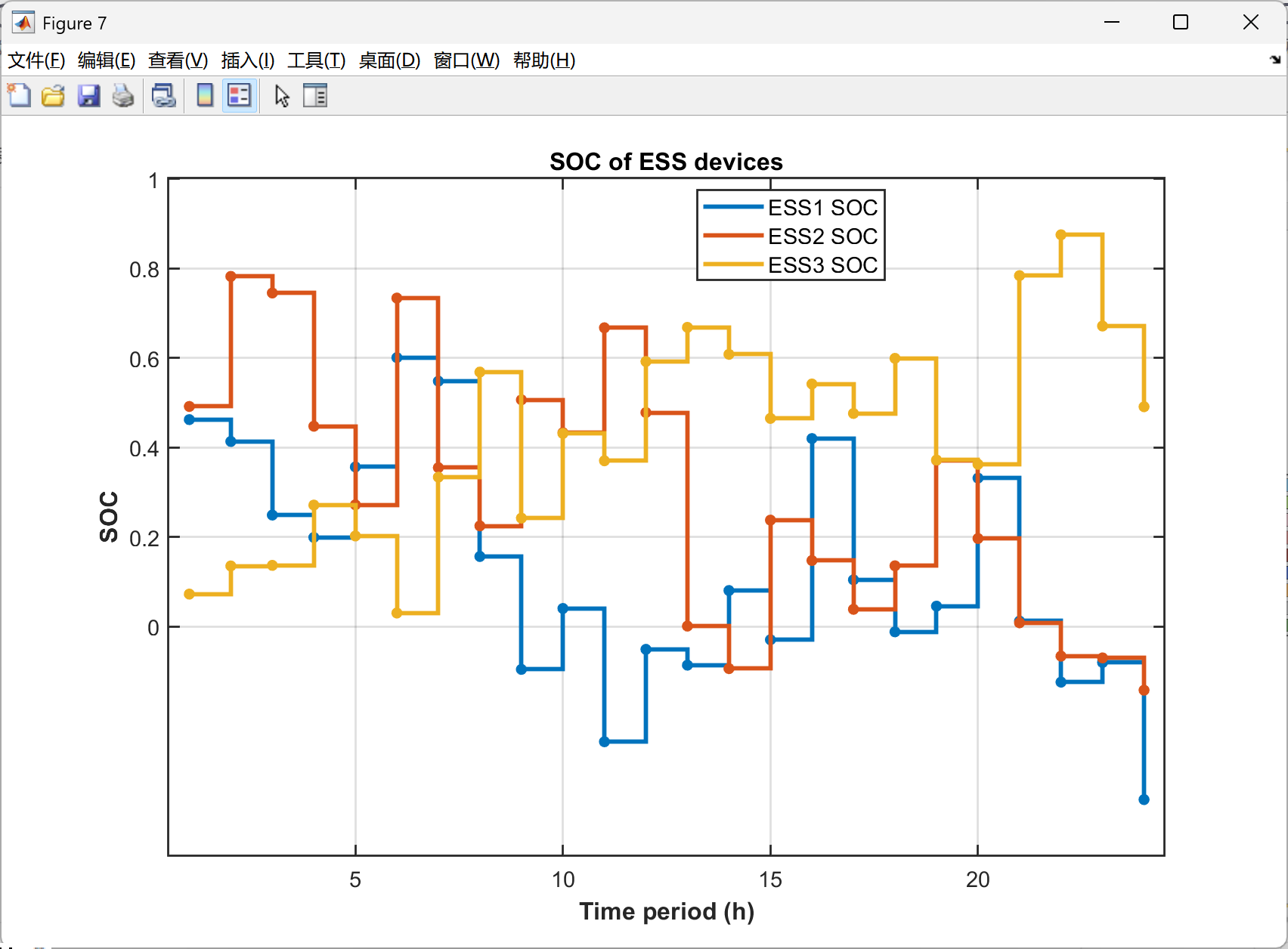
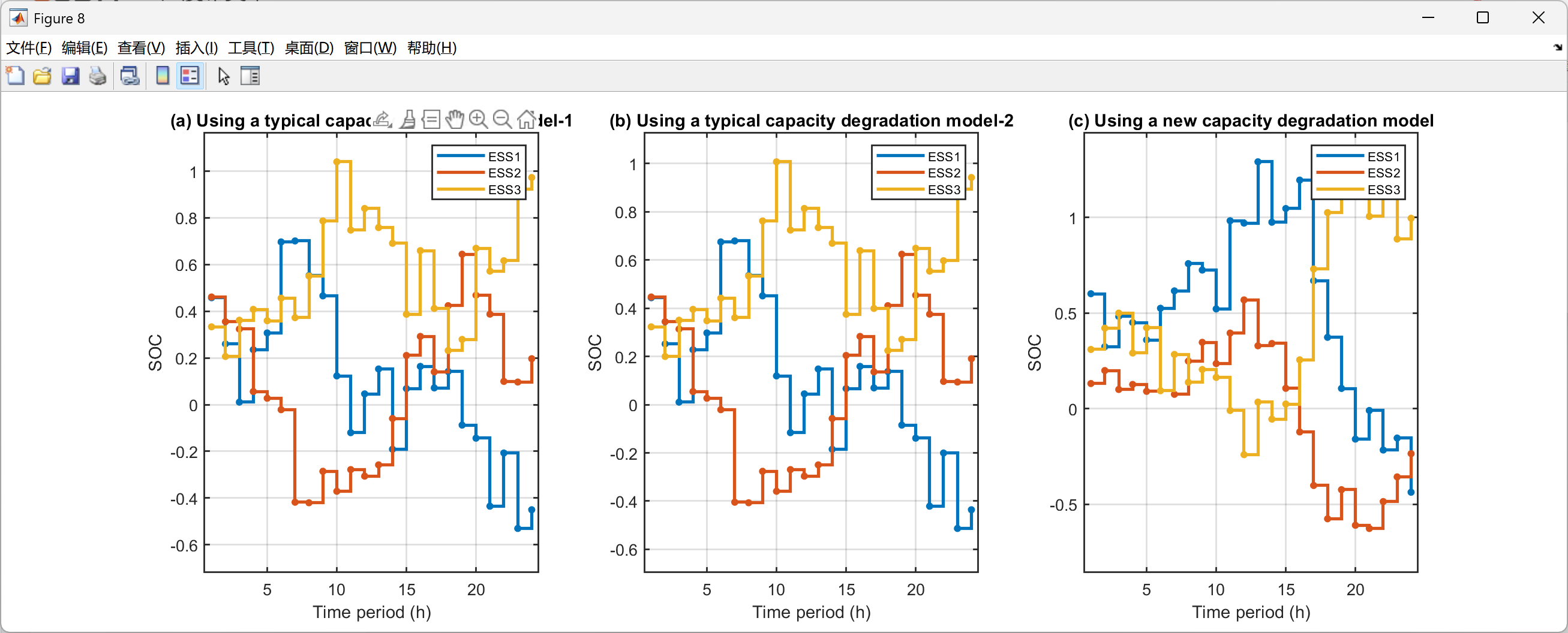
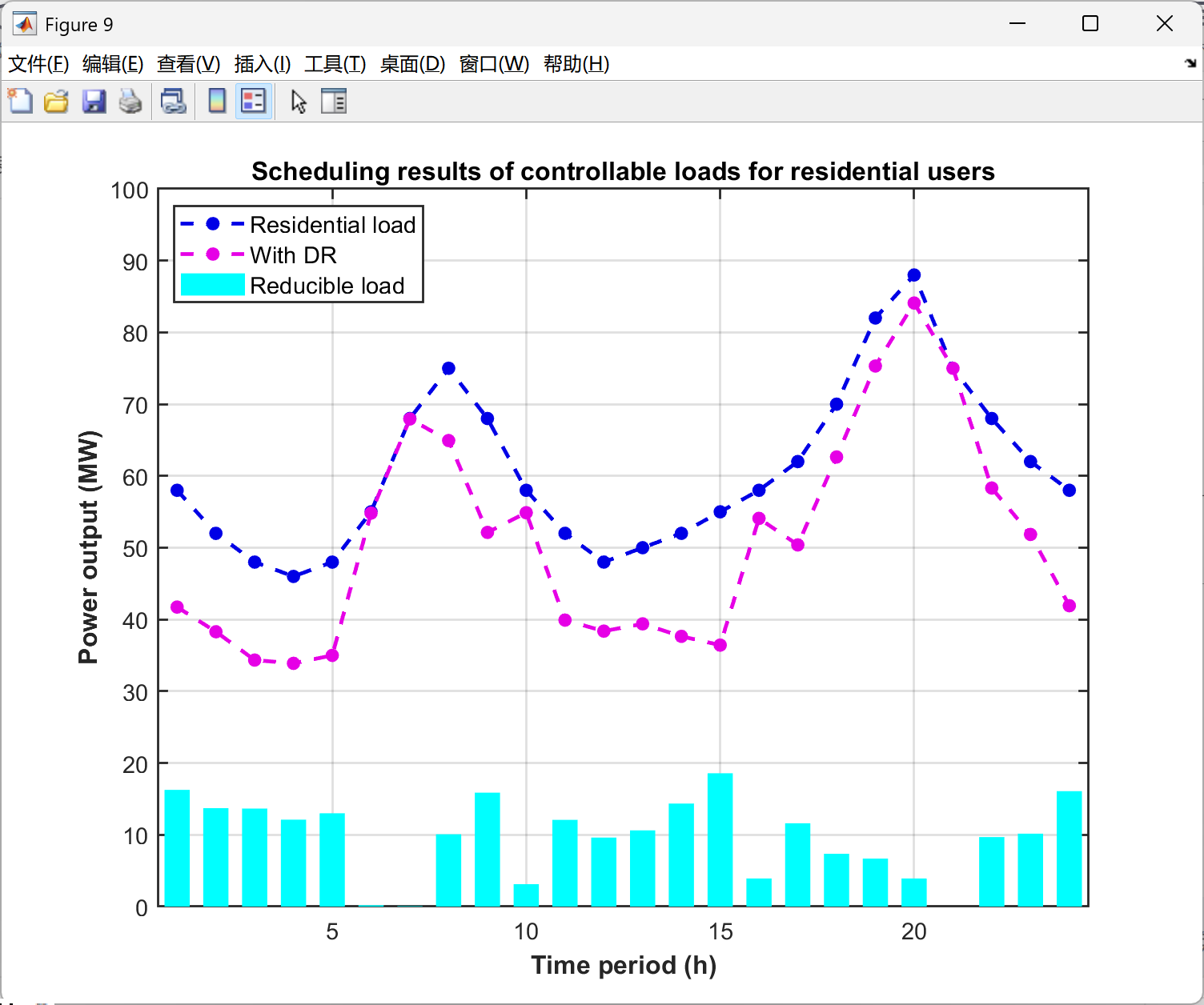
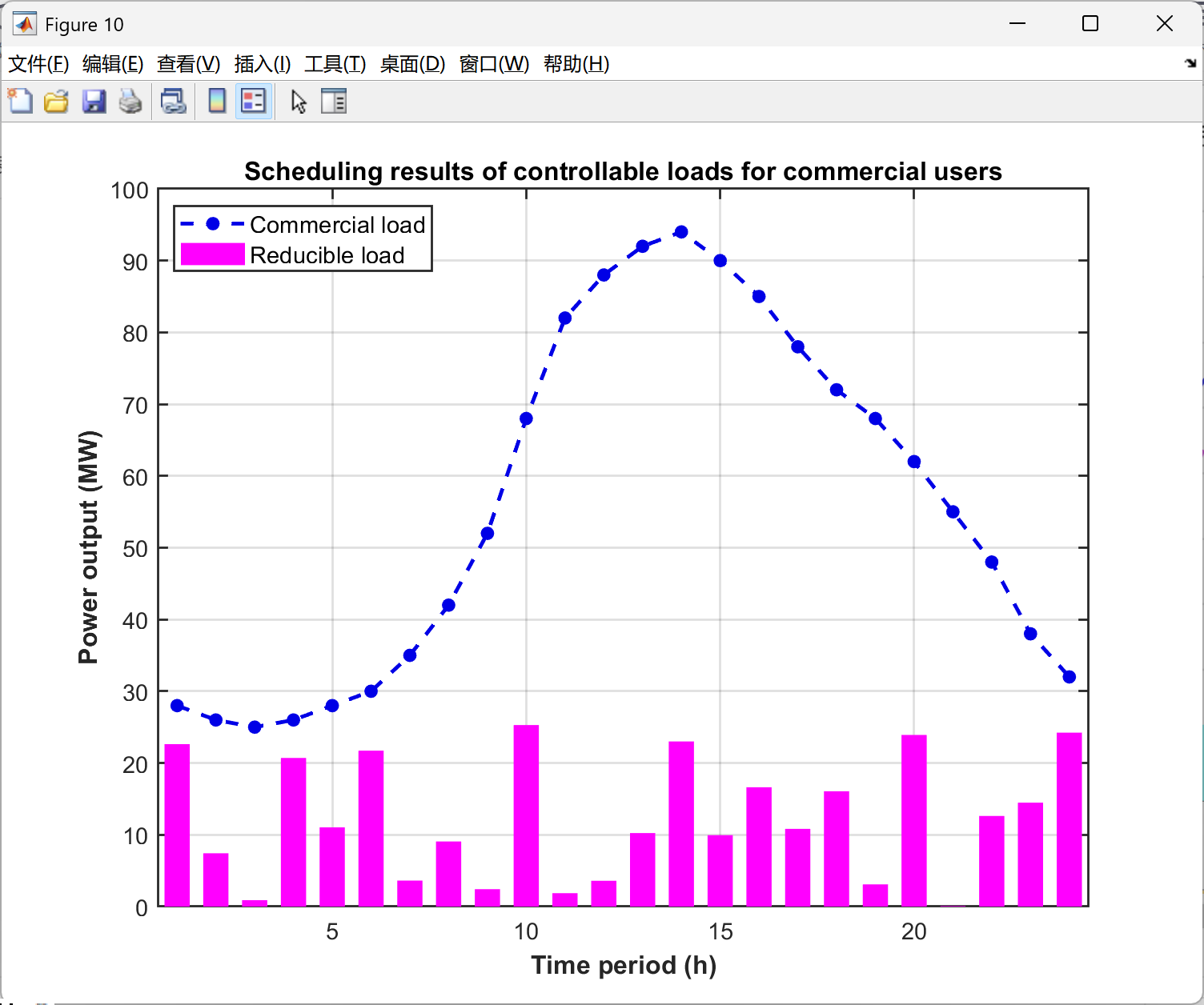
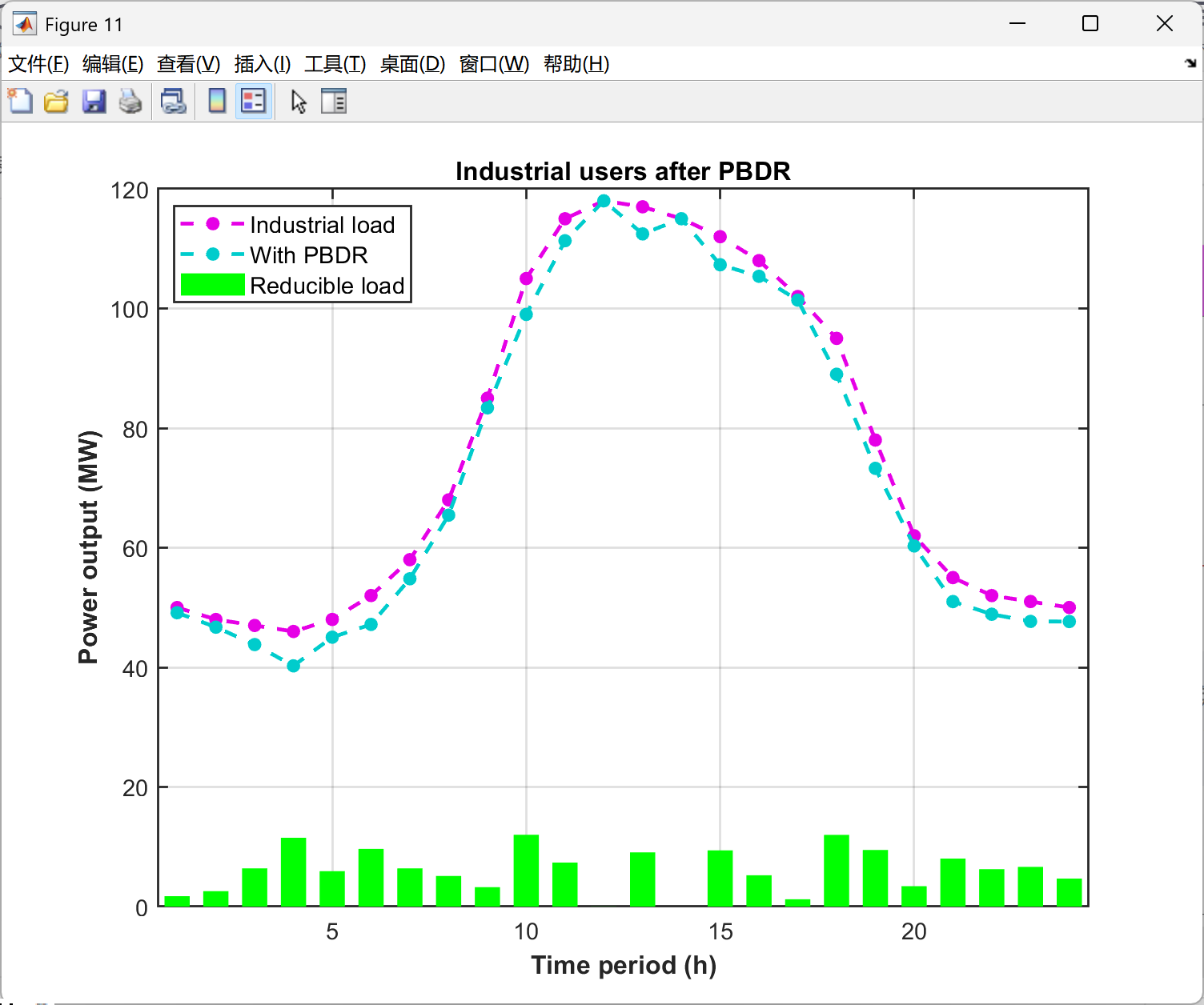
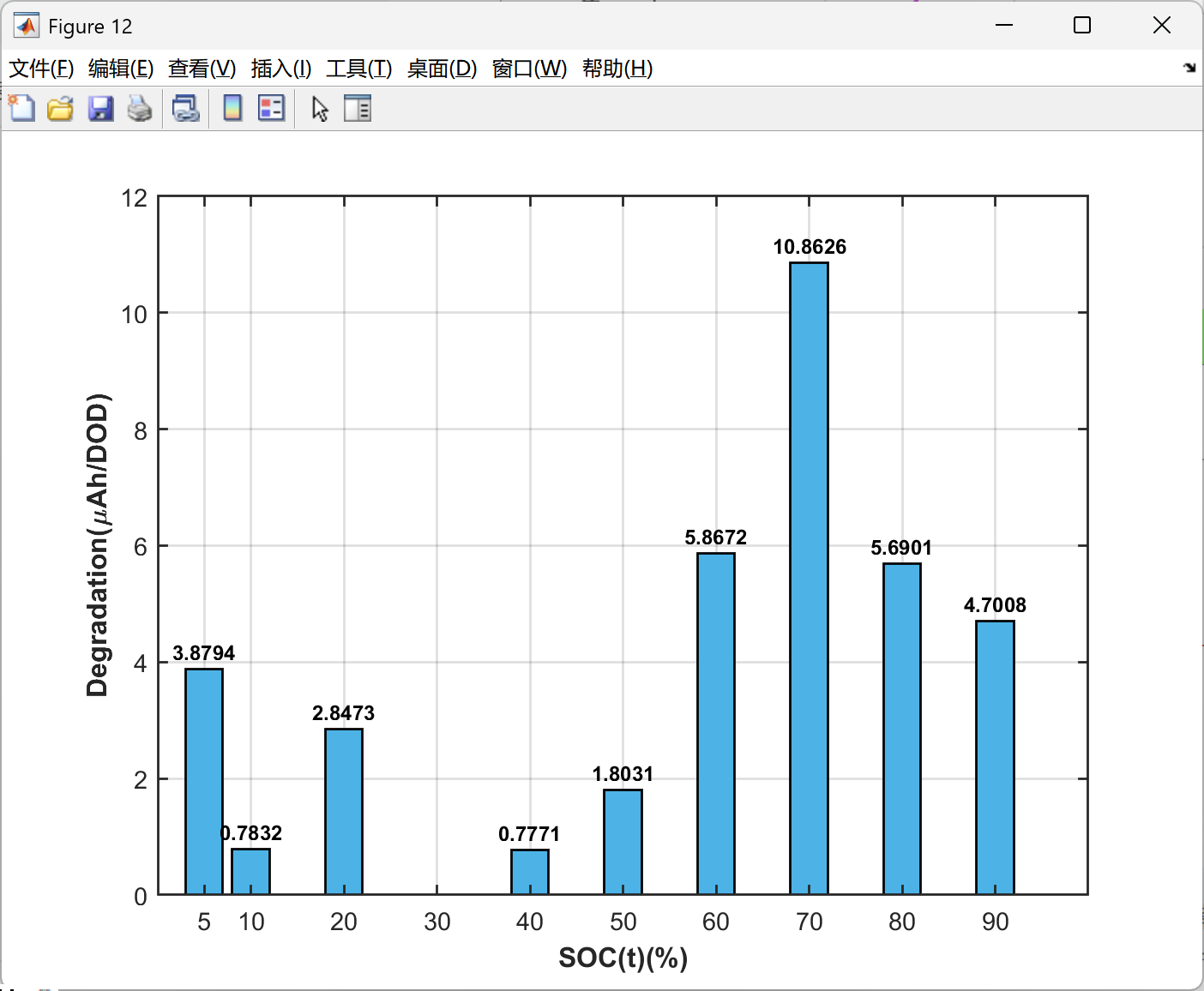
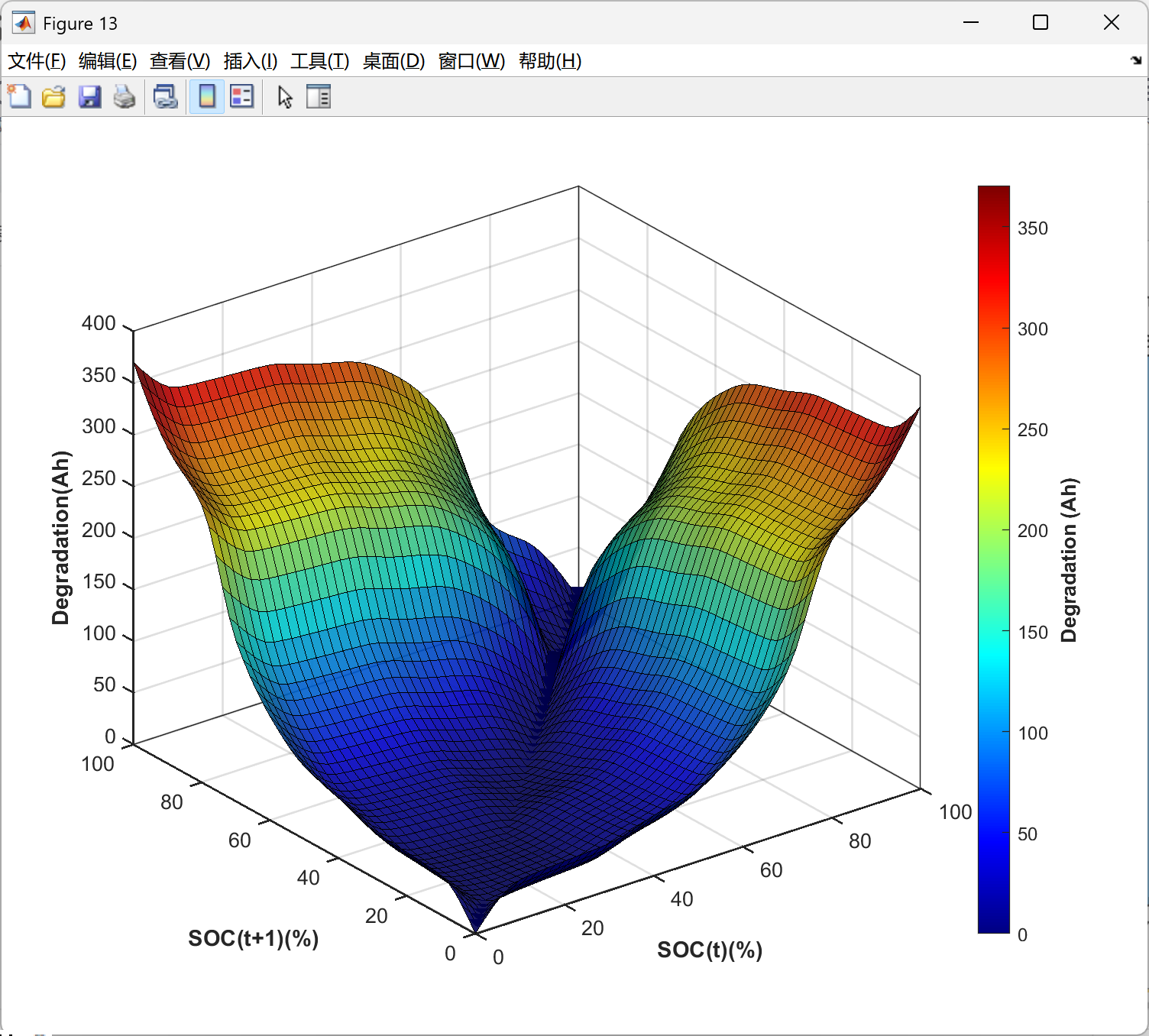
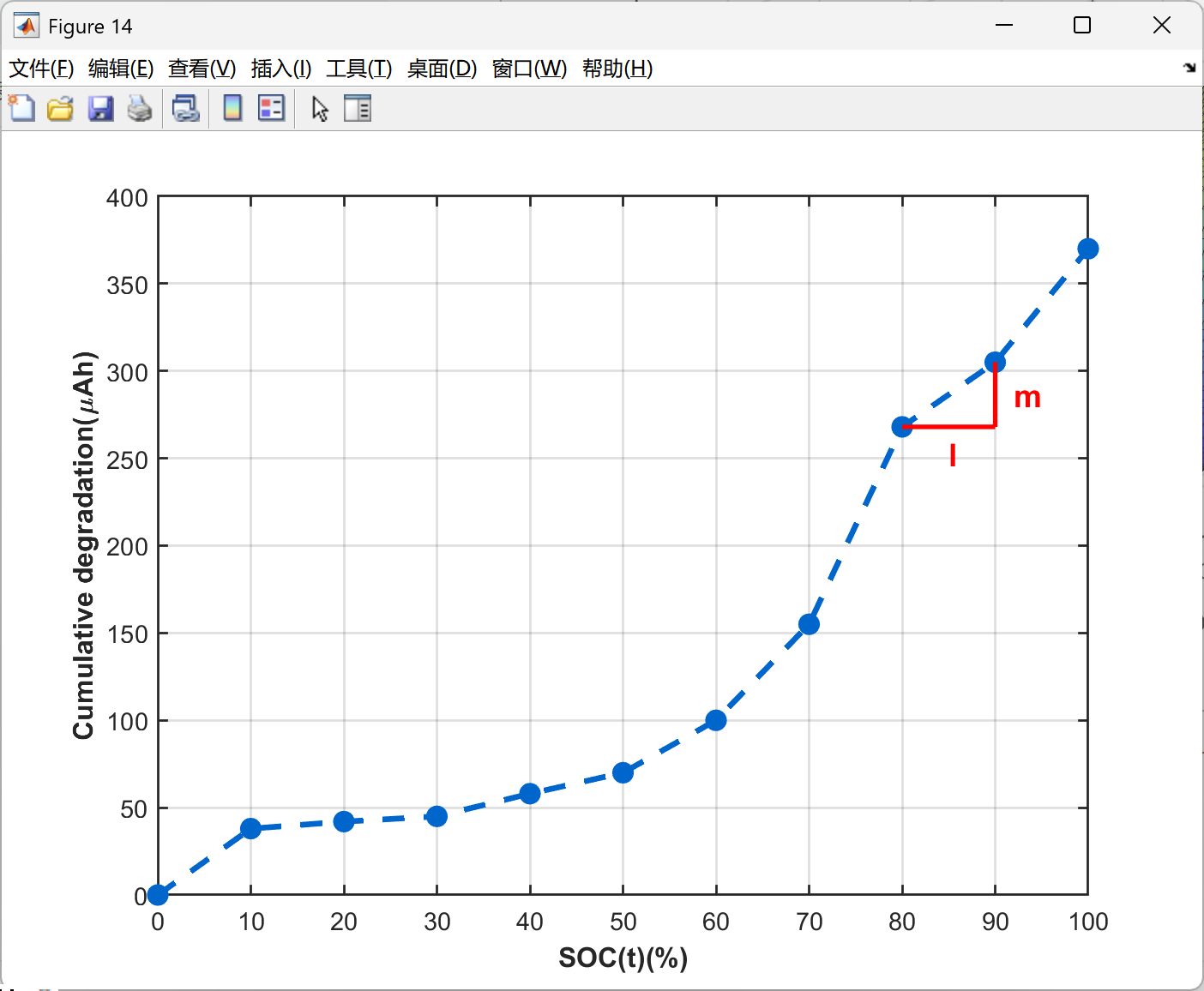
以上求解为局部最优,下面的求解结果是继续优化的代码,获得了全局最优解,误差很小很小,点赞!复现了很久,辛苦是值得的。
为了美观,后面的运行结果图去掉Matlab图框
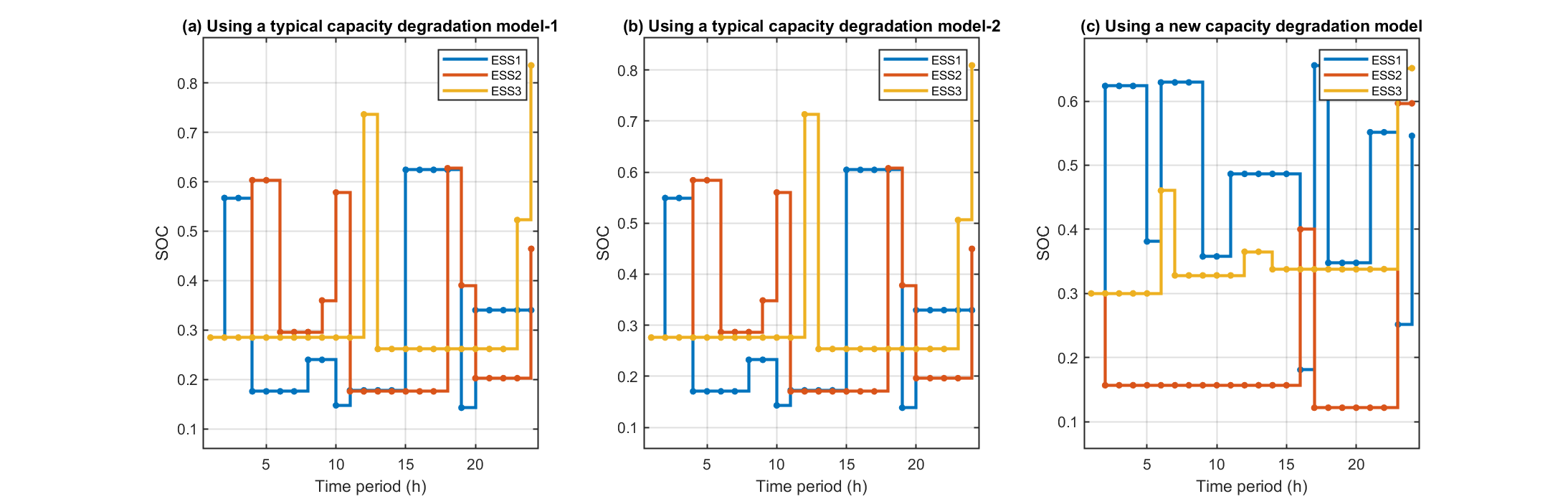
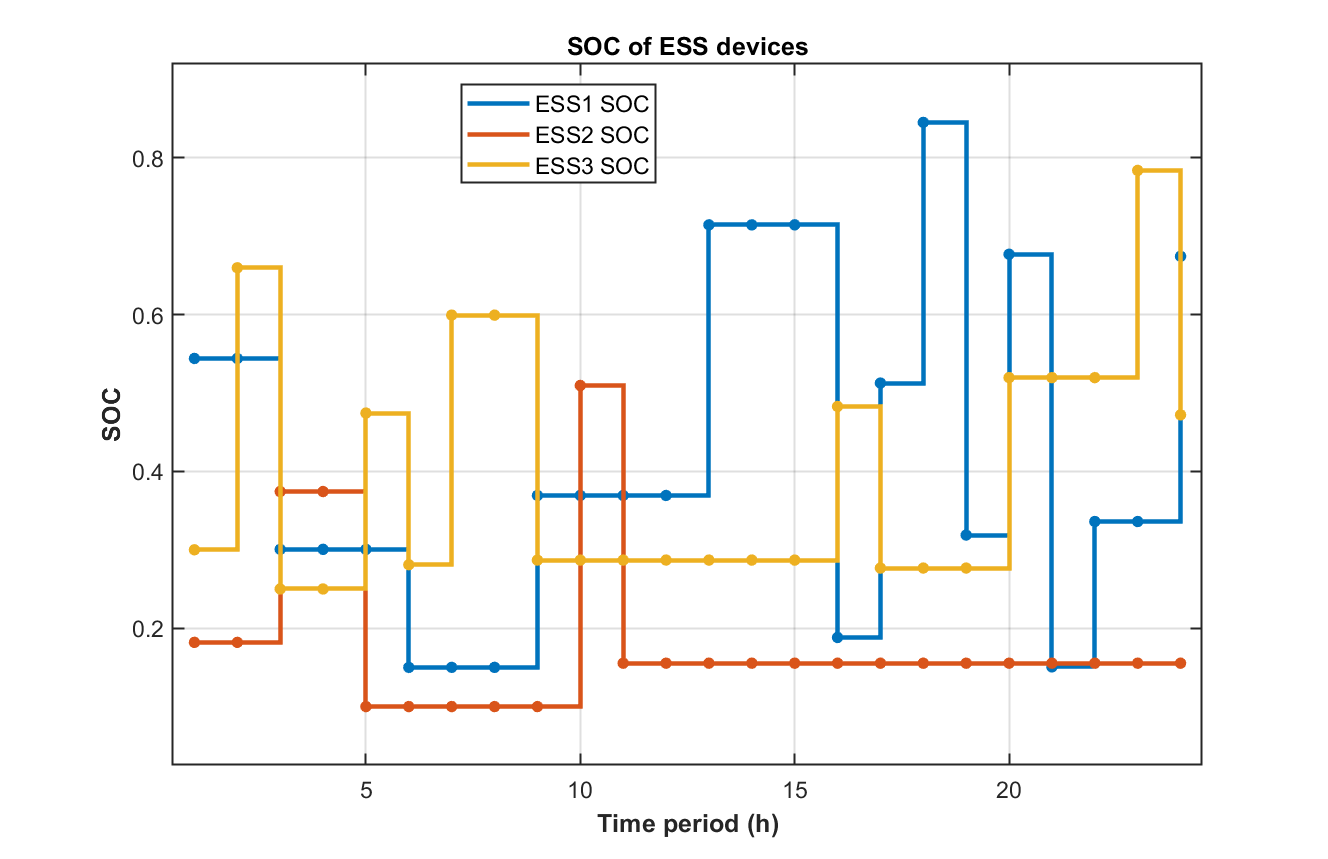
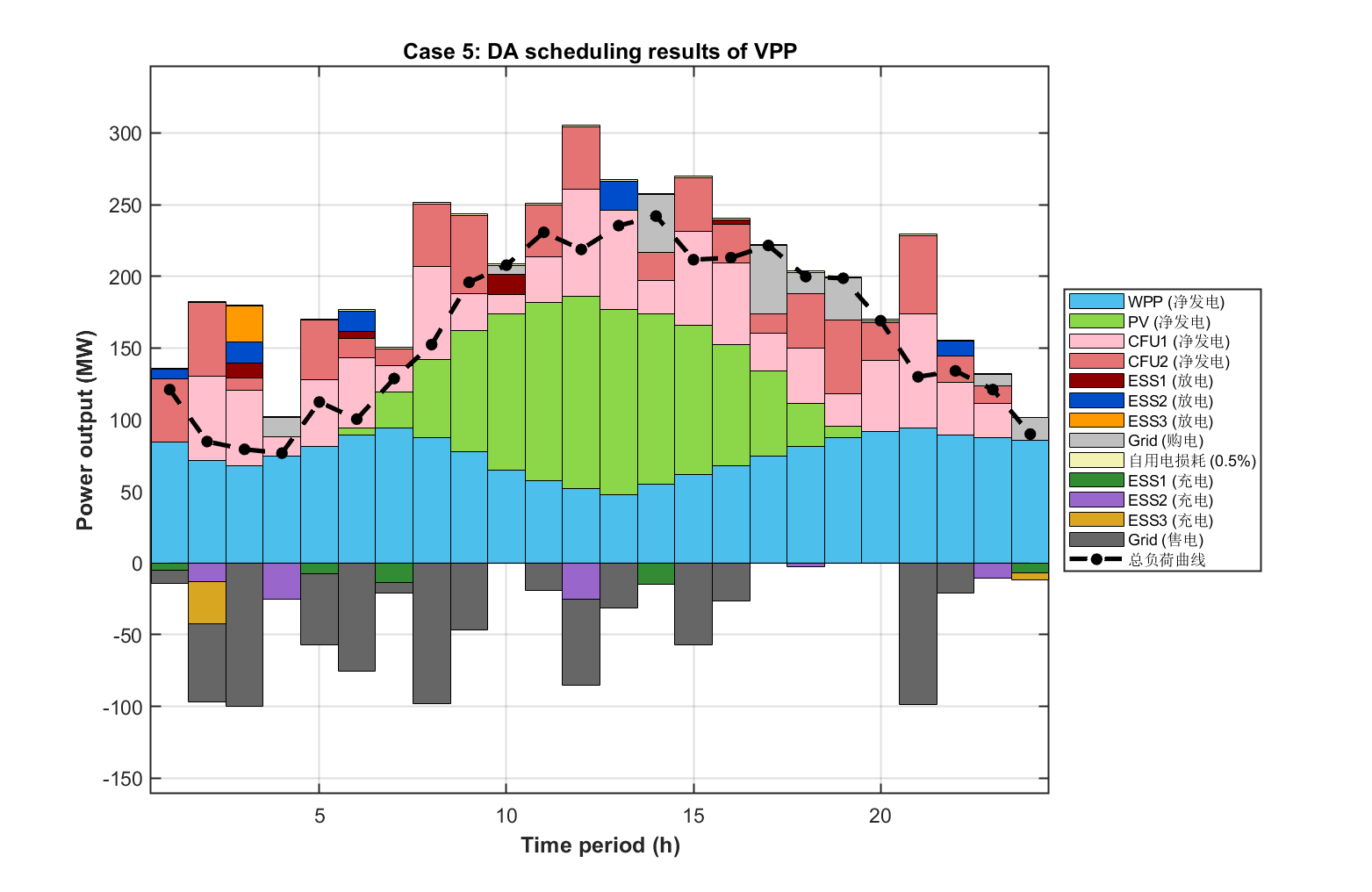
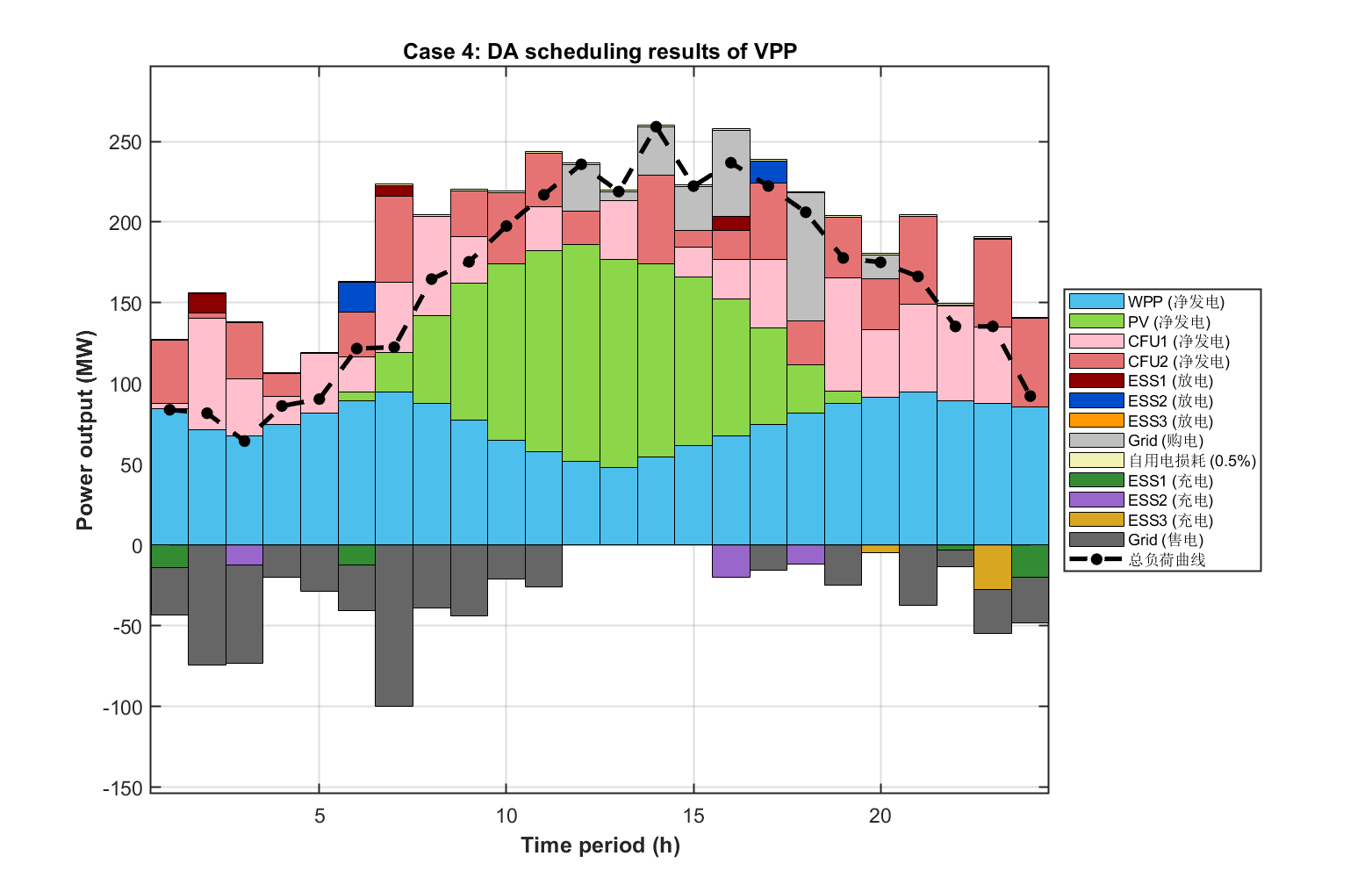
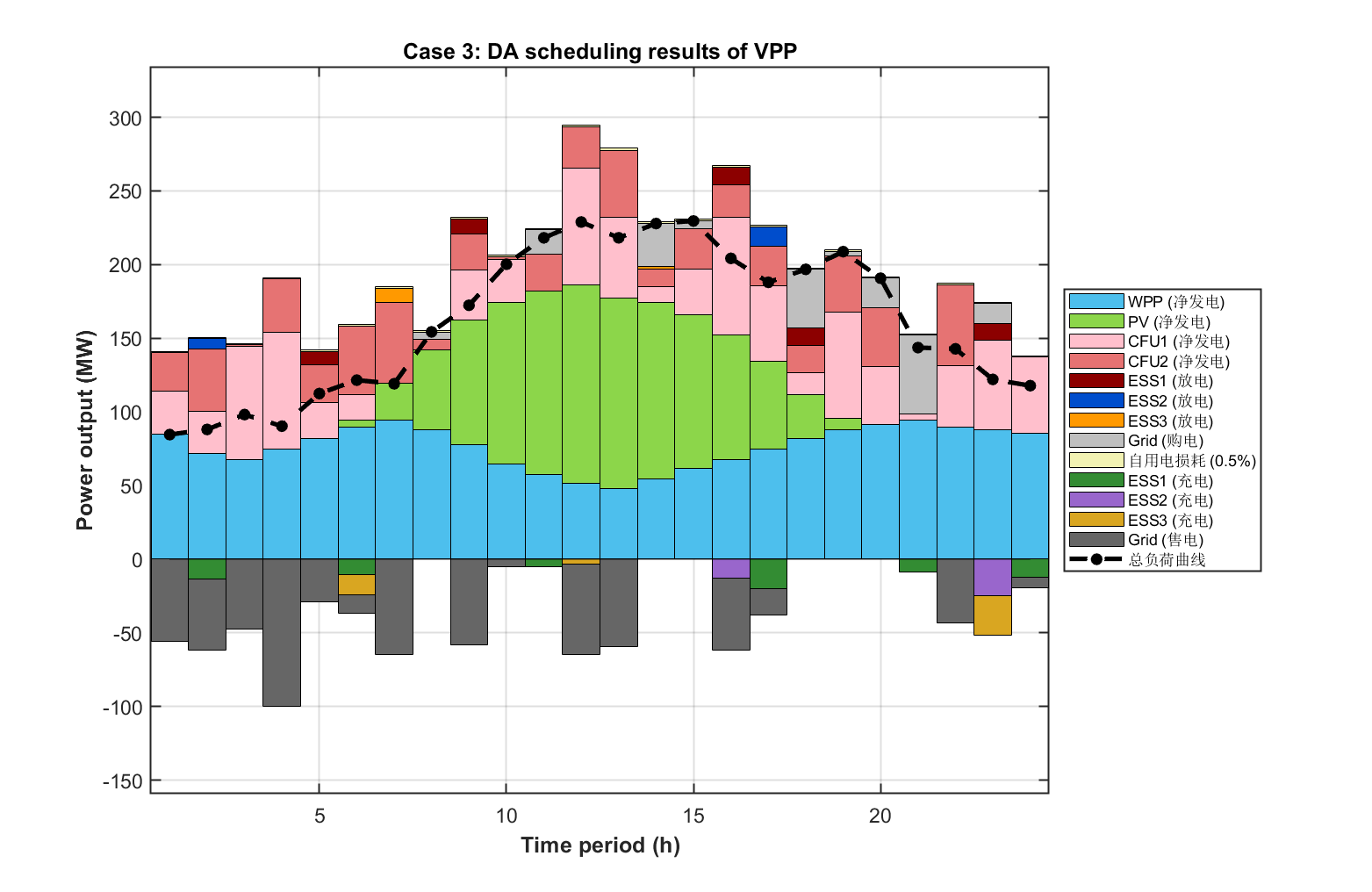
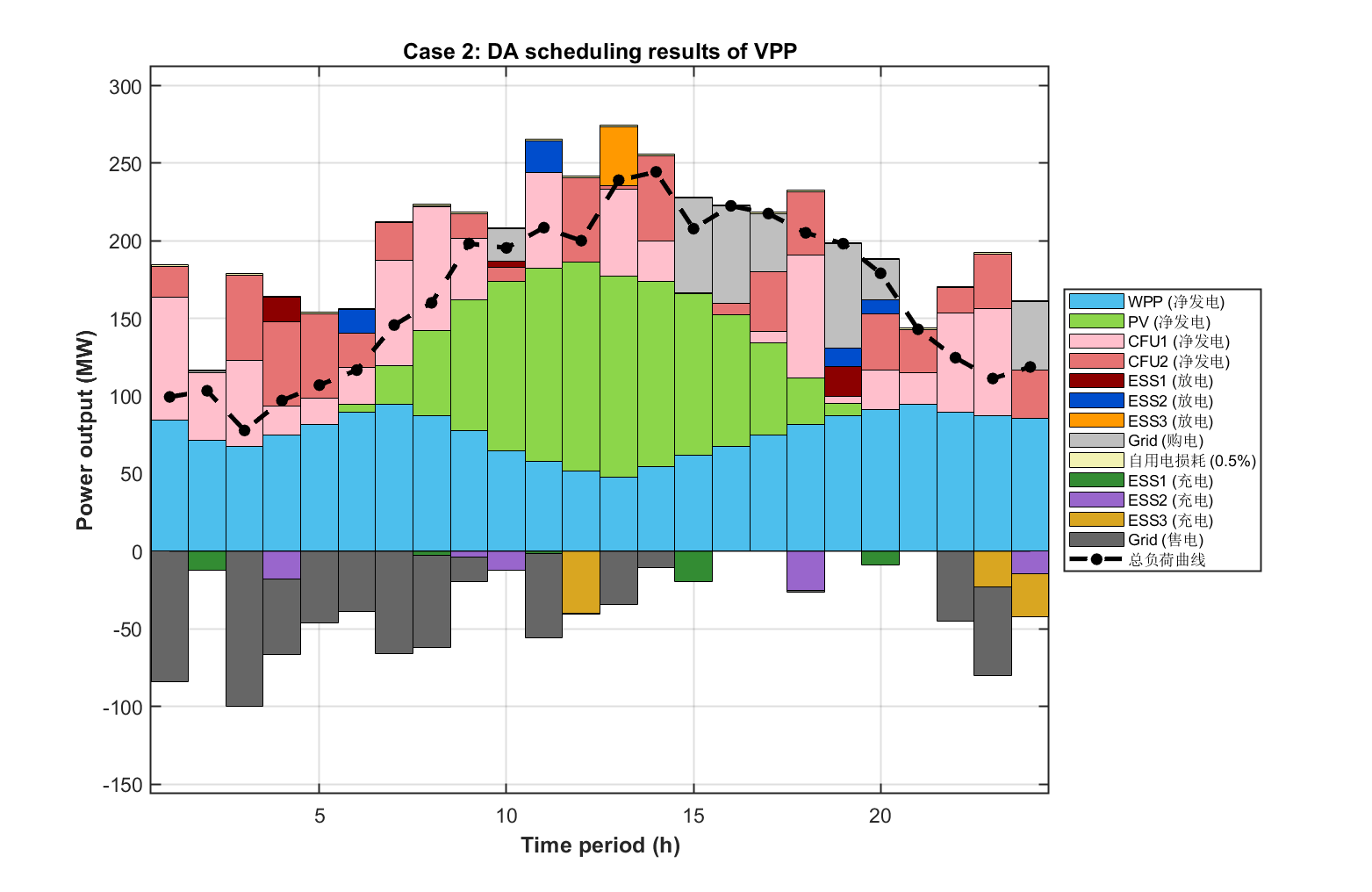
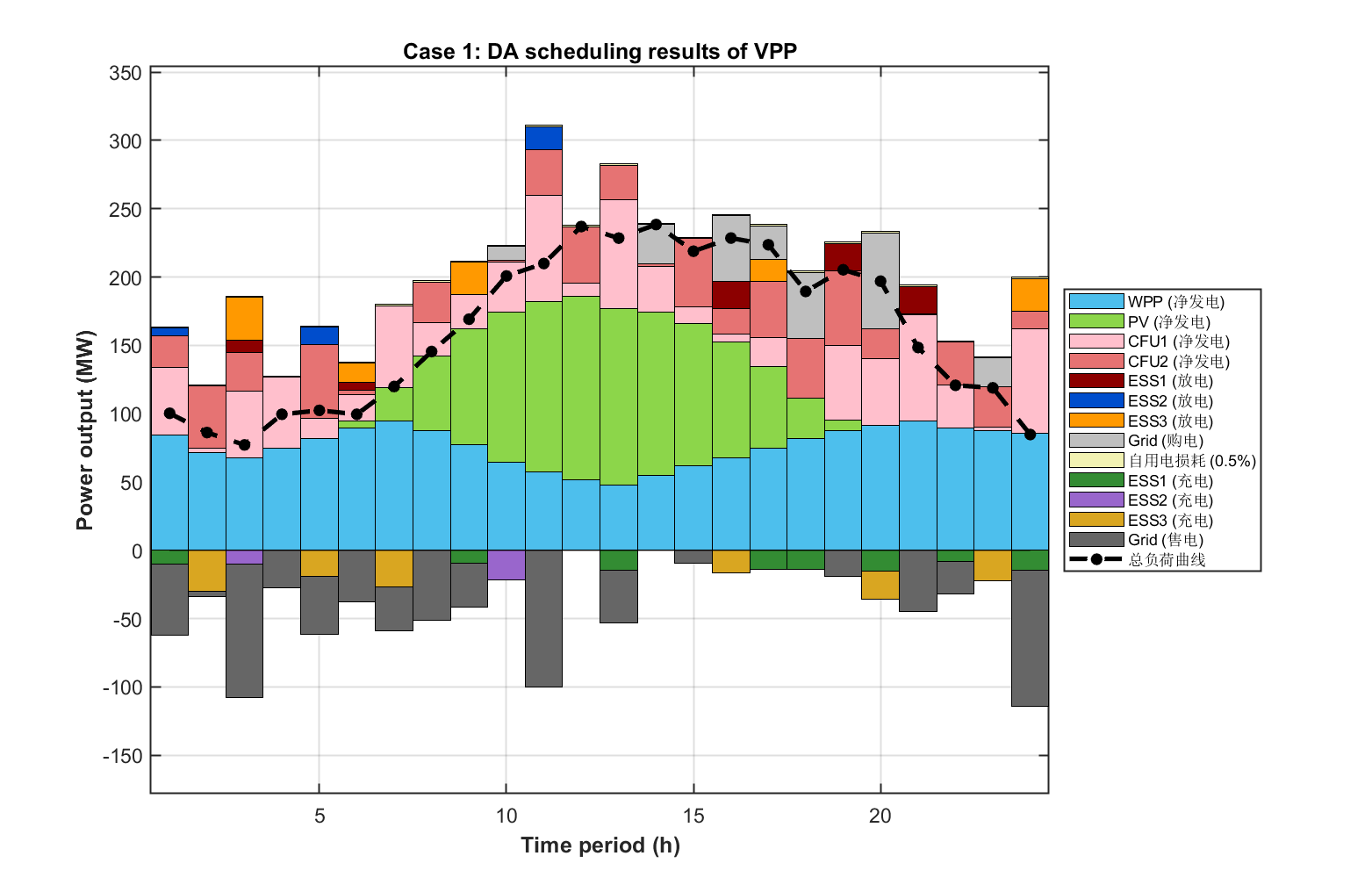

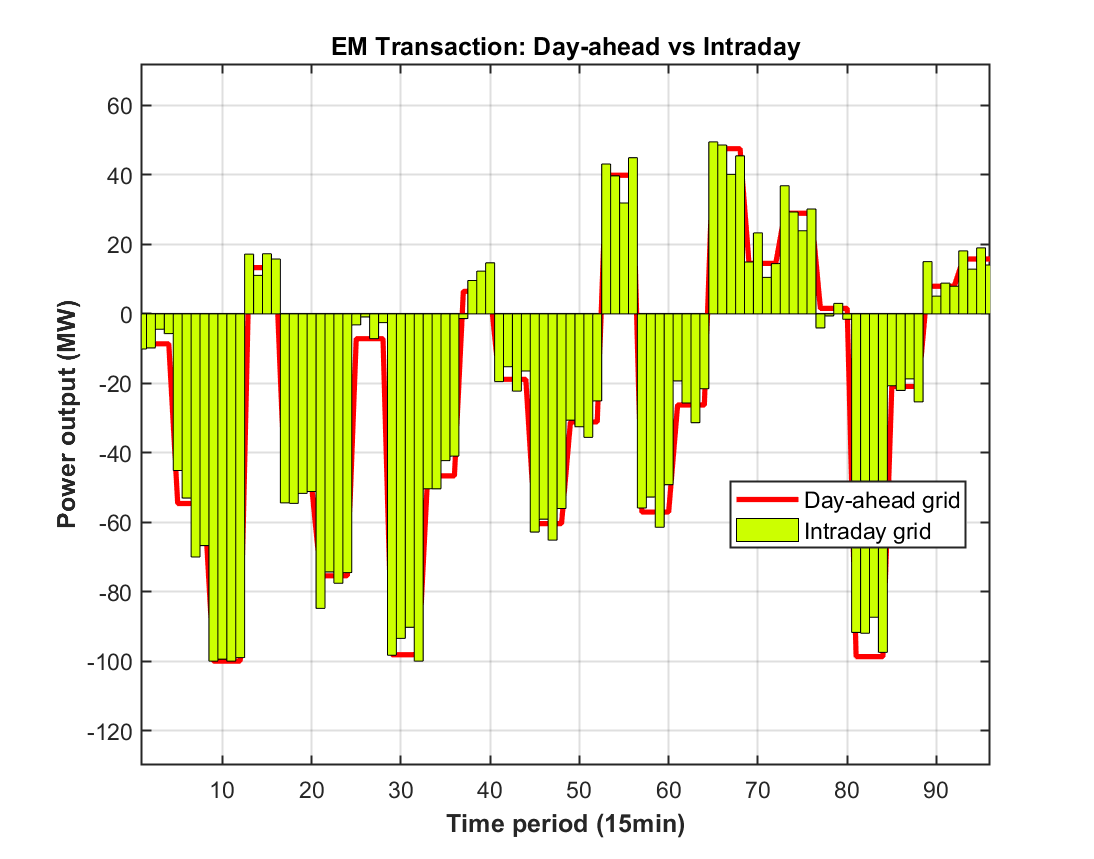



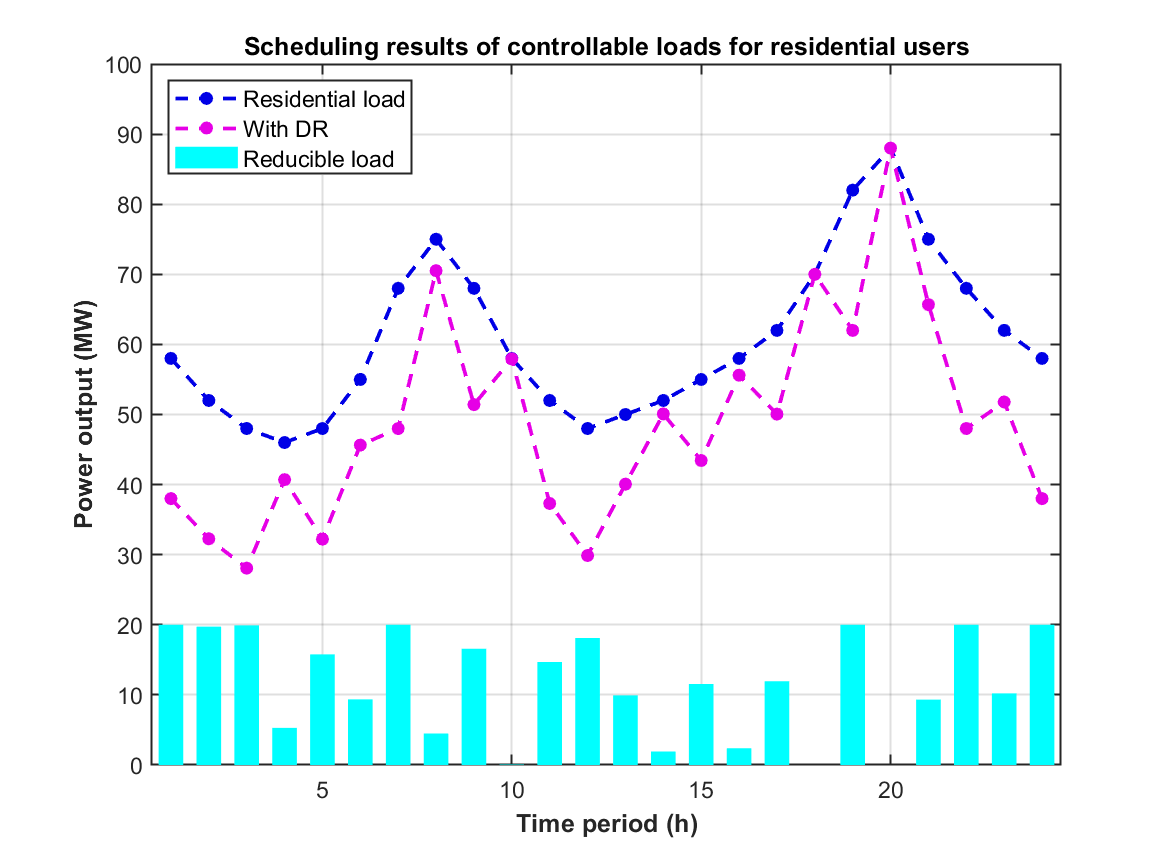
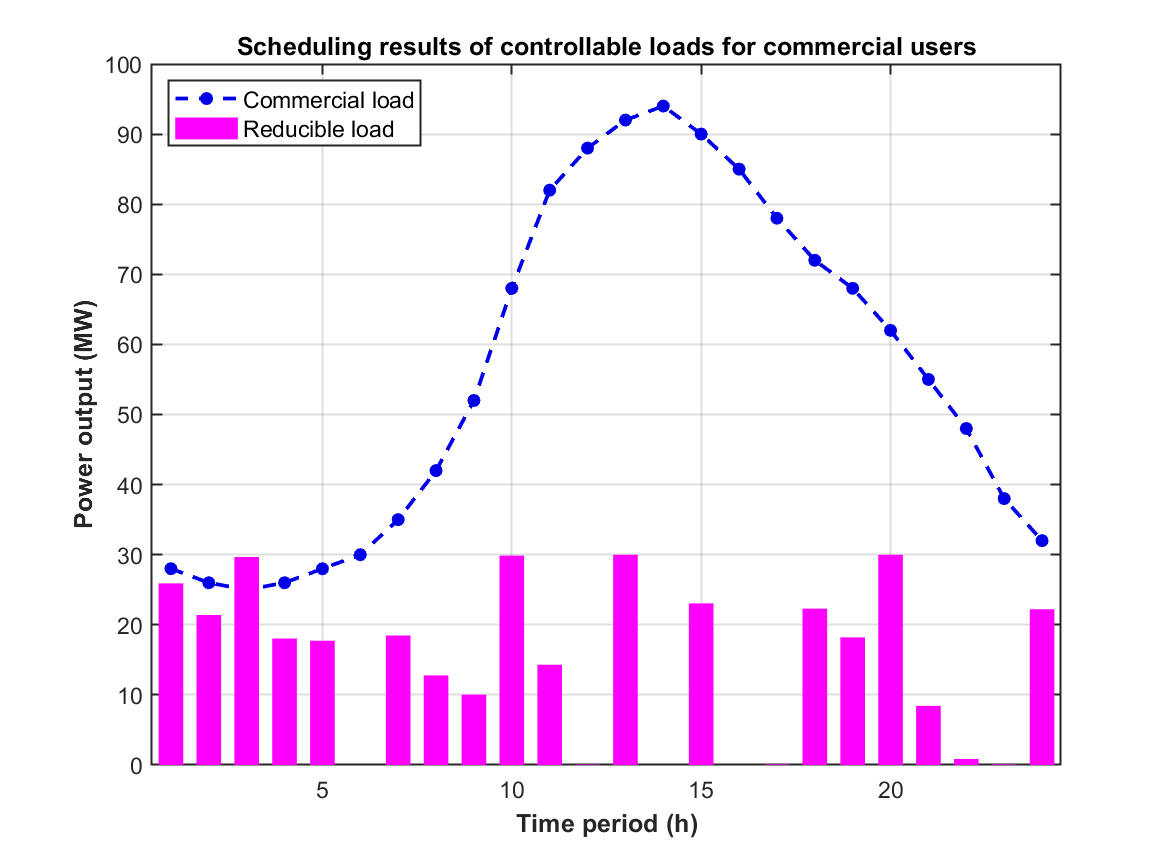
部分代码:
function PlotIntradayFigures(Data, Result_DA)
% 生成日内调度图表
% 输入: Data-系统参数, Result_DA-日前调度结果
fprintf(' 正在生成日内调度图表...\n');
PlotFig16_IntradayForecast(Data); % 日内预测曲线
PlotFig17_CFU_Comparison(Data, Result_DA); % CFU日前日内对比
PlotFig18_ESS_Comparison(Data, Result_DA); % ESS日前日内对比
PlotFig19_EM_Comparison(Data, Result_DA); % EM交易日前日内对比
fprintf(' 日内调度图表生成完成!\n');
end
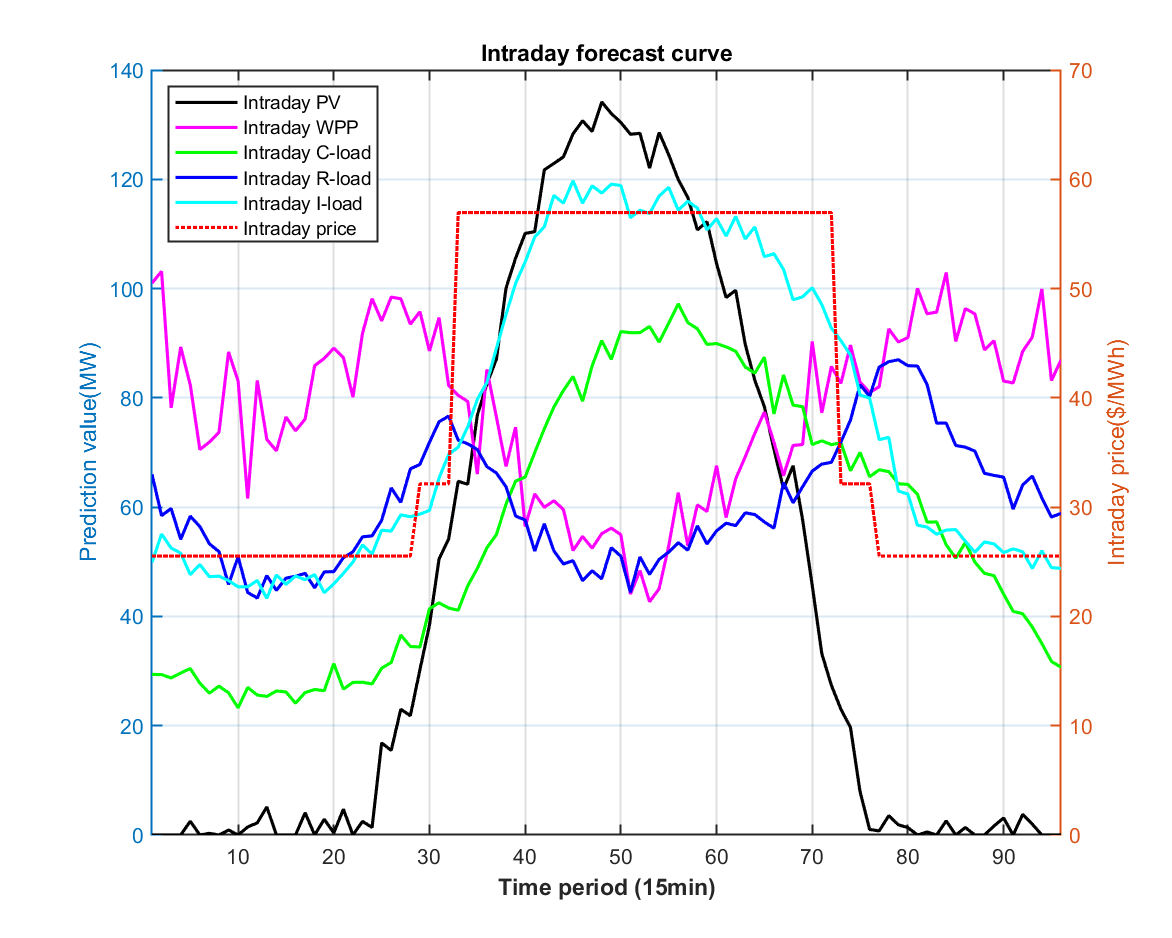
%% 图16: 日内预测曲线
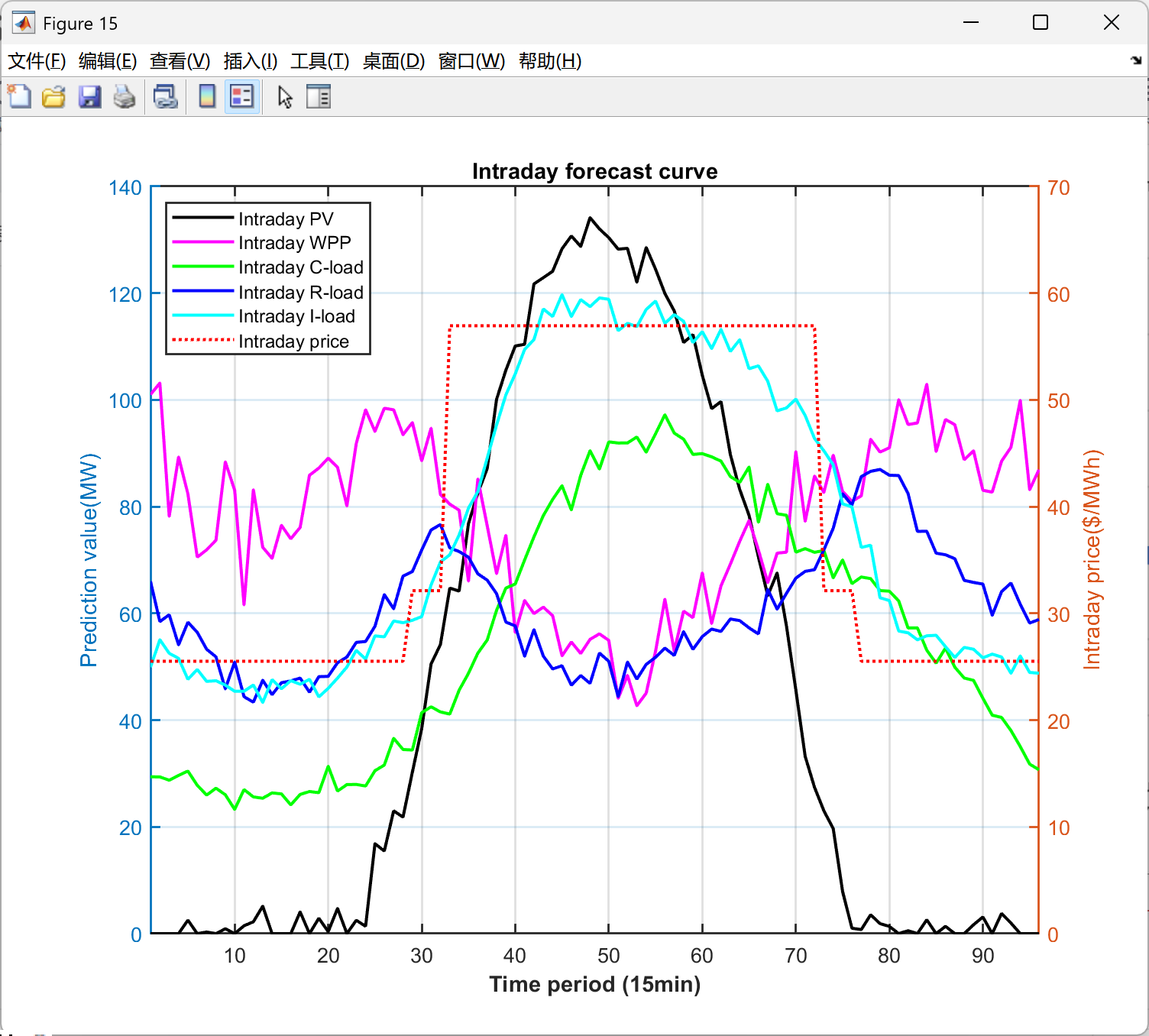
function PlotFig16_IntradayForecast(Data)
fig = figure('Position', [100, 100, 750, 600]);
set(fig, 'Color', 'w');
t_ID = 1:96; % 96个15分钟时段
% 左Y轴: 功率预测
yyaxis left
plot(t_ID, Data.P_PV_ID, '-', 'Color', [0 0 0], 'LineWidth', 1.5); hold on; % 光伏
plot(t_ID, Data.P_WPP_ID, '-', 'Color', [1 0 1], 'LineWidth', 1.5); % 风电
plot(t_ID, Data.P_load_C_ID, '-', 'Color', [0 1 0], 'LineWidth', 1.5); % 商业负荷
plot(t_ID, Data.P_load_R_ID, '-', 'Color', [0 0 1], 'LineWidth', 1.5); % 居民负荷
plot(t_ID, Data.P_load_I_ID, '-', 'Color', [0 1 1], 'LineWidth', 1.5); % 工业负荷
ylabel('Prediction value(MW)', 'FontSize', 11);
ylim([0 140]);
% 右Y轴: 电价
yyaxis right
plot(t_ID, Data.lambda_pur_ID, ':', 'Color', [1 0 0], 'LineWidth', 1.5);
ylabel('Intraday price($/MWh)', 'FontSize', 11);
ylim([0 70]);
xlabel('Time period (15min)', 'FontSize', 12, 'FontWeight', 'bold');
title('Intraday forecast curve', 'FontSize', 13, 'FontWeight', 'bold');
legend({'Intraday PV', 'Intraday WPP', 'Intraday C-load', 'Intraday R-load', 'Intraday I-load', 'Intraday price'}, ...
'Location', 'northwest', 'FontSize', 9);
grid on; box on;
xlim([1, 96]);
set(gca, 'FontSize', 10, 'LineWidth', 1);
saveas(fig, 'Figures/Fig16_Intraday_Forecast.png');
end
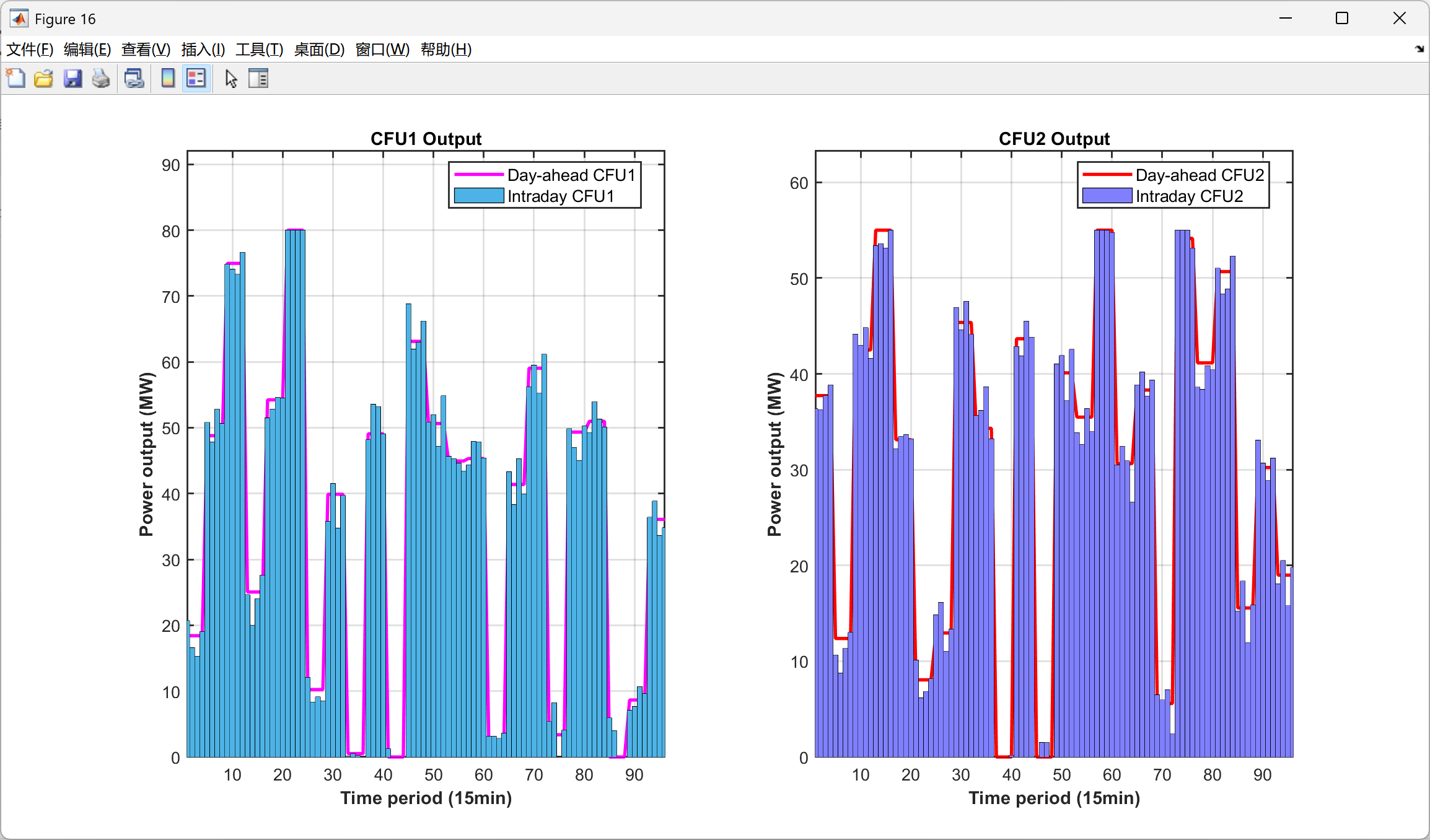
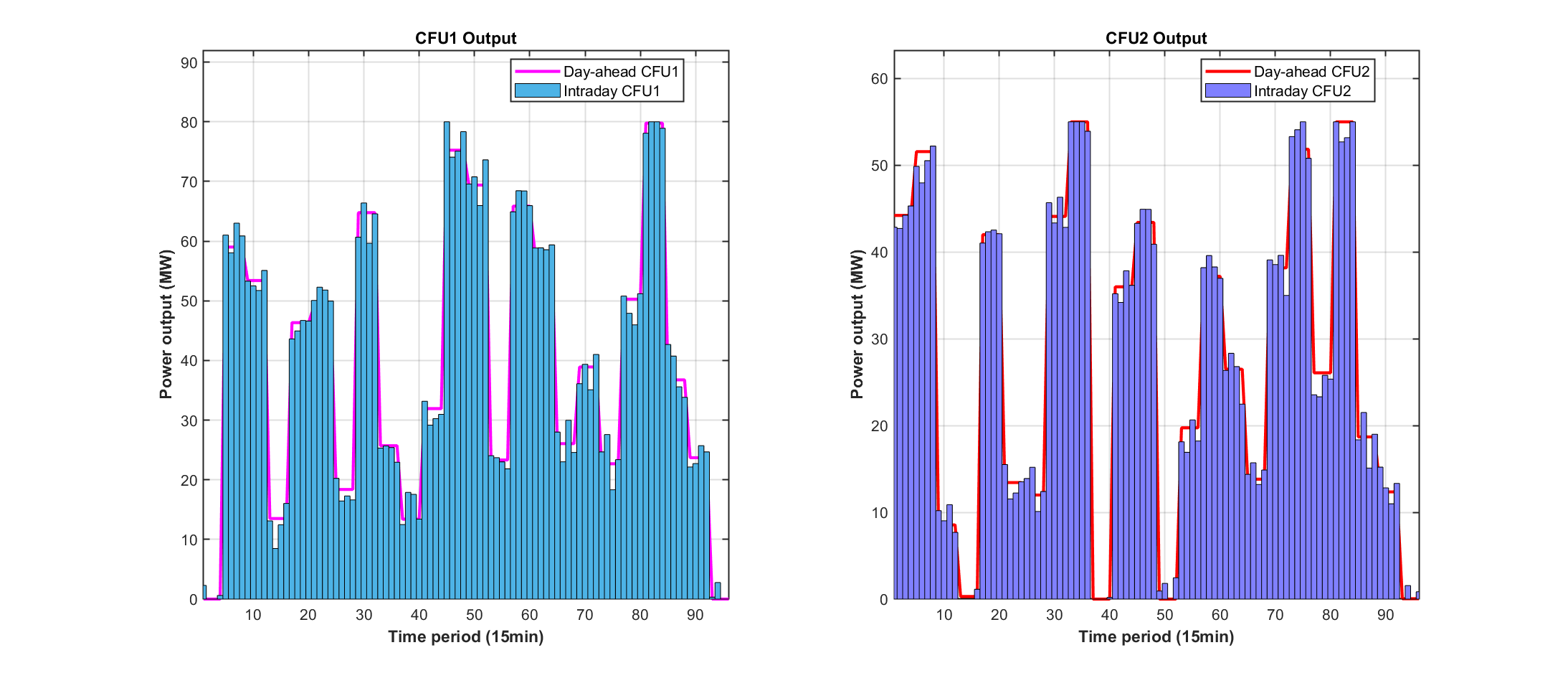
%% 图17: CFU日前日内对比
function PlotFig17_CFU_Comparison(Data, R)
% 模拟日内调度结果(在日前基础上增加随机波动)
rng(123);
P_CFU1_ID = repelem(R.P_DG(1,:), 4) + randn(1, 96) * 3; % 将24时段扩展到96时段并加波动
P_CFU2_ID = repelem(R.P_DG(2,:), 4) + randn(1, 96) * 2;
P_CFU1_ID = max(0, min(P_CFU1_ID, Data.DG(1).P_max)); % 限制在可行范围
P_CFU2_ID = max(0, min(P_CFU2_ID, Data.DG(2).P_max));
fig = figure('Position', [100, 100, 1400, 600]);
set(fig, 'Color', 'w');
t_ID = 1:96;
subplot(1, 2, 1);
hold on; box on; grid on;
plot(t_ID, repelem(R.P_DG(1,:), 4), '-', 'Color', [1 0 1], 'LineWidth', 2); % 日前计划
bar(t_ID, P_CFU1_ID, 'FaceColor', [0.3 0.7 0.9], 'EdgeColor', 'k', 'LineWidth', 0.5, 'BarWidth', 1); % 日内实际
xlabel('Time period (15min)', 'FontSize', 11, 'FontWeight', 'bold');
ylabel('Power output (MW)', 'FontSize', 11, 'FontWeight', 'bold');
title('CFU1 Output', 'FontSize', 12, 'FontWeight', 'bold');
legend('Day-ahead CFU1', 'Intraday CFU1', 'Location', 'best', 'FontSize', 10);
xlim([1, 96]);
% 自动计算Y轴范围
cfu1_max = max([P_CFU1_ID, repelem(R.P_DG(1,:), 4)]);
ylim([0, cfu1_max * 1.15]);
set(gca, 'FontSize', 10, 'LineWidth', 1);
subplot(1, 2, 2);
hold on; box on; grid on;
plot(t_ID, repelem(R.P_DG(2,:), 4), '-', 'Color', [1 0 0], 'LineWidth', 2); % 日前计划
bar(t_ID, P_CFU2_ID, 'FaceColor', [0.5 0.5 1], 'EdgeColor', 'k', 'LineWidth', 0.5, 'BarWidth', 1); % 日内实际
xlabel('Time period (15min)', 'FontSize', 11, 'FontWeight', 'bold');
ylabel('Power output (MW)', 'FontSize', 11, 'FontWeight', 'bold');
title('CFU2 Output', 'FontSize', 12, 'FontWeight', 'bold');
legend('Day-ahead CFU2', 'Intraday CFU2', 'Location', 'best', 'FontSize', 10);
xlim([1, 96]);
% 自动计算Y轴范围
cfu2_max = max([P_CFU2_ID, repelem(R.P_DG(2,:), 4)]);
ylim([0, cfu2_max * 1.15]);
set(gca, 'FontSize', 10, 'LineWidth', 1);
saveas(fig, 'Figures/Fig17_CFU_Comparison.png');
end
%% 图18: ESS日前日内对比
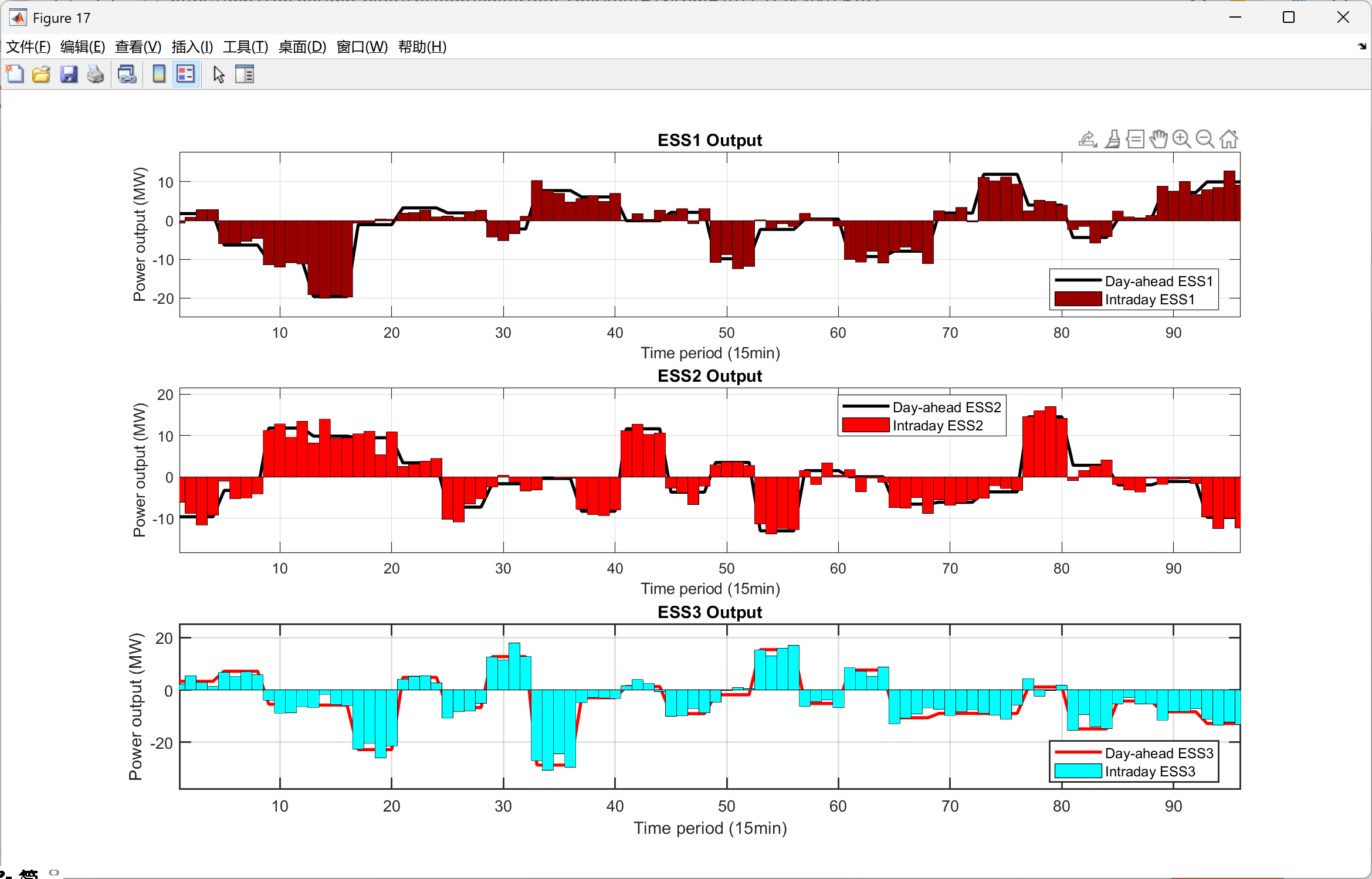
function PlotFig18_ESS_Comparison(Data, R)
% 模拟日内调度(在日前基础上加波动)
rng(456);
P_ESS1_ID = repelem(R.P_ESS_dis(1,:) - R.P_ESS_ch(1,:), 4) + randn(1, 96) * 1.5;
P_ESS2_ID = repelem(R.P_ESS_dis(2,:) - R.P_ESS_ch(2,:), 4) + randn(1, 96) * 1.5;
P_ESS3_ID = repelem(R.P_ESS_dis(3,:) - R.P_ESS_ch(3,:), 4) + randn(1, 96) * 2;
% 限制在充放电功率范围内
P_ESS1_ID = max(-Data.ESS(1).P_ch_max, min(P_ESS1_ID, Data.ESS(1).P_dis_max));
P_ESS2_ID = max(-Data.ESS(2).P_ch_max, min(P_ESS2_ID, Data.ESS(2).P_dis_max));
P_ESS3_ID = max(-Data.ESS(3).P_ch_max, min(P_ESS3_ID, Data.ESS(3).P_dis_max));
fig = figure('Position', [100, 100, 1400, 1000]);
set(fig, 'Color', 'w');
t_ID = 1:96;
subplot(3, 1, 1);
hold on; box on; grid on;
P_ESS1_DA = R.P_ESS_dis(1,:) - R.P_ESS_ch(1,:); % 日前净功率
plot(t_ID, repelem(P_ESS1_DA, 4), '-', 'Color', [0 0 0], 'LineWidth', 2); % 日前计划
bar(t_ID, P_ESS1_ID, 'FaceColor', [0.6 0 0], 'EdgeColor', 'k', 'LineWidth', 0.5, 'BarWidth', 1); % 日内实际
xlabel('Time period (15min)', 'FontSize', 10);
ylabel('Power output (MW)', 'FontSize', 10);
title('ESS1 Output', 'FontSize', 11, 'FontWeight', 'bold');
legend('Day-ahead ESS1', 'Intraday ESS1', 'Location', 'best', 'FontSize', 9);
xlim([1, 96]);
ess1_min = min([P_ESS1_ID, repelem(P_ESS1_DA, 4)]);
ess1_max = max([P_ESS1_ID, repelem(P_ESS1_DA, 4)]);
ess1_range = ess1_max - ess1_min;
ylim([ess1_min - 0.15*ess1_range, ess1_max + 0.15*ess1_range]);
subplot(3, 1, 2);
hold on; box on; grid on;
P_ESS2_DA = R.P_ESS_dis(2,:) - R.P_ESS_ch(2,:);
plot(t_ID, repelem(P_ESS2_DA, 4), '-', 'Color', [0 0 0], 'LineWidth', 2);
bar(t_ID, P_ESS2_ID, 'FaceColor', [1 0 0], 'EdgeColor', 'k', 'LineWidth', 0.5, 'BarWidth', 1);
xlabel('Time period (15min)', 'FontSize', 10);
ylabel('Power output (MW)', 'FontSize', 10);
title('ESS2 Output', 'FontSize', 11, 'FontWeight', 'bold');
legend('Day-ahead ESS2', 'Intraday ESS2', 'Location', 'best', 'FontSize', 9);
xlim([1, 96]);
ess2_min = min([P_ESS2_ID, repelem(P_ESS2_DA, 4)]);
ess2_max = max([P_ESS2_ID, repelem(P_ESS2_DA, 4)]);
ess2_range = ess2_max - ess2_min;
ylim([ess2_min - 0.15*ess2_range, ess2_max + 0.15*ess2_range]);
subplot(3, 1, 3);
hold on; box on; grid on;
P_ESS3_DA = R.P_ESS_dis(3,:) - R.P_ESS_ch(3,:);
plot(t_ID, repelem(P_ESS3_DA, 4), '-', 'Color', [1 0 0], 'LineWidth', 2);
bar(t_ID, P_ESS3_ID, 'FaceColor', [0 1 1], 'EdgeColor', 'k', 'LineWidth', 0.5, 'BarWidth', 1);
xlabel('Time period (15min)', 'FontSize', 10);
ylabel('Power output (MW)', 'FontSize', 10);
title('ESS3 Output', 'FontSize', 11, 'FontWeight', 'bold');
legend('Day-ahead ESS3', 'Intraday ESS3', 'Location', 'best', 'FontSize', 9);
xlim([1, 96]);
ess3_min = min([P_ESS3_ID, repelem(P_ESS3_DA, 4)]);
ess3_max = max([P_ESS3_ID, repelem(P_ESS3_DA, 4)]);
ess3_range = ess3_max - ess3_min;
ylim([ess3_min - 0.15*ess3_range, ess3_max + 0.15*ess3_range]);
set(gca, 'FontSize', 10, 'LineWidth', 1);
saveas(fig, 'Figures/Fig18_ESS_Comparison.png');
end
%% 图19: EM交易日前日内对比
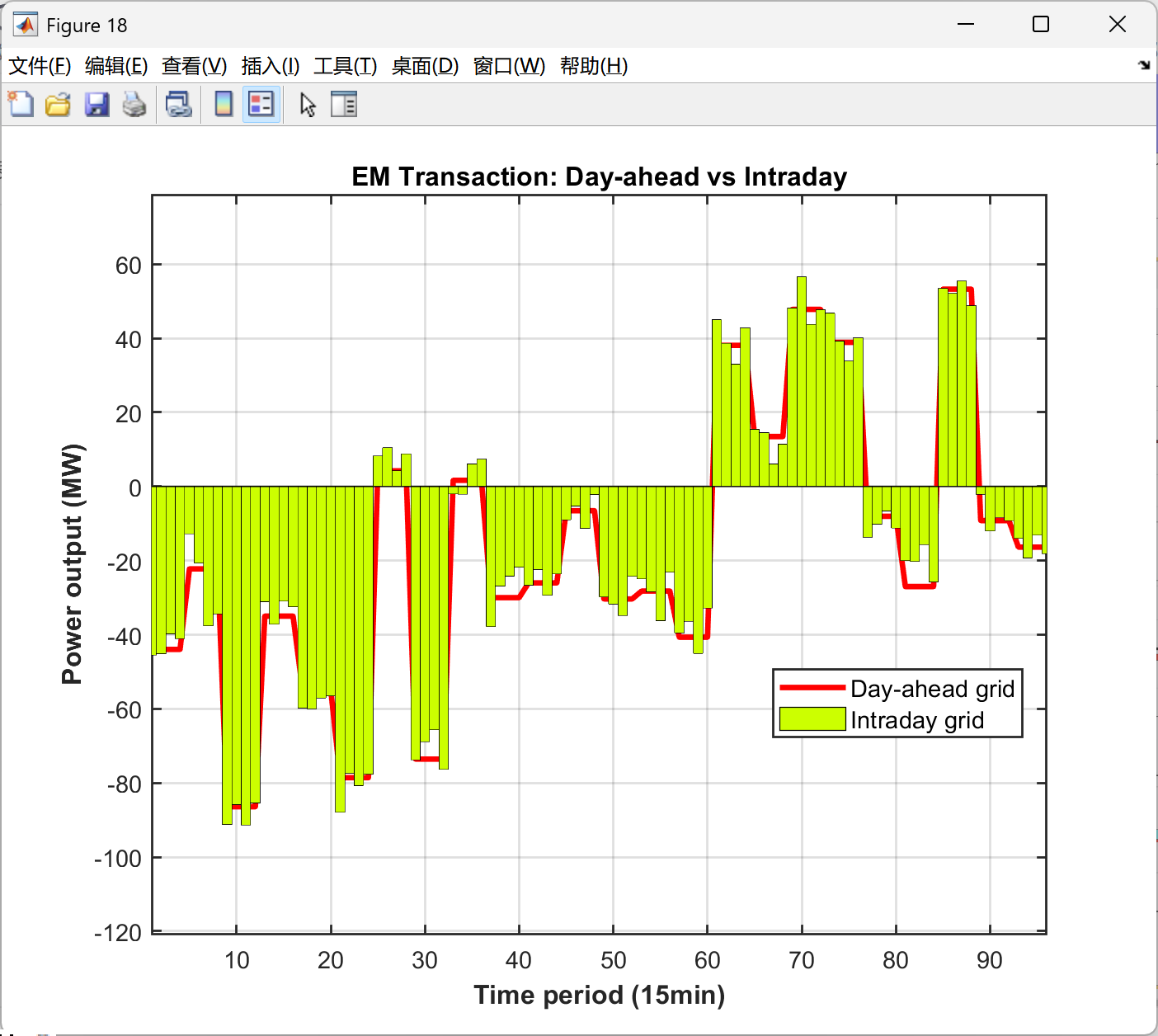
function PlotFig19_EM_Comparison(Data, R)
% 模拟日内调度(在日前基础上加波动)
rng(789);
P_EM_ID = repelem(R.P_EM, 4) + randn(1, 96) * 5;
P_EM_ID = max(-100, min(P_EM_ID, 100)); % 限制交易功率
fig = figure('Position', [100, 100, 700, 550]);
set(fig, 'Color', 'w');
t_ID = 1:96;
hold on; box on; grid on;
plot(t_ID, repelem(R.P_EM, 4), '-', 'Color', [1 0 0], 'LineWidth', 2.5); % 日前计划
bar(t_ID, P_EM_ID, 'FaceColor', [0.8 1 0], 'EdgeColor', 'k', 'LineWidth', 0.5, 'BarWidth', 1); % 日内实际
plot([1 96], [0 0], 'k-', 'LineWidth', 0.5); % 零线
xlabel('Time period (15min)', 'FontSize', 12, 'FontWeight', 'bold');
ylabel('Power output (MW)', 'FontSize', 12, 'FontWeight', 'bold');
title('EM Transaction: Day-ahead vs Intraday', 'FontSize', 13, 'FontWeight', 'bold');
legend('Day-ahead grid', 'Intraday grid', 'Location', 'best', 'FontSize', 11);
xlim([1, 96]);
% 自动计算Y轴范围
em_min = min([P_EM_ID, repelem(R.P_EM, 4)]);
em_max = max([P_EM_ID, repelem(R.P_EM, 4)]);
em_range = em_max - em_min;
ylim([em_min - 0.2*em_range, em_max + 0.15*em_range]);
set(gca, 'FontSize', 11, 'LineWidth', 1);
saveas(fig, 'Figures/Fig19_EM_Comparison.png');
end
🎉3 参考文献
文章中一些内容引自网络,会注明出处或引用为参考文献,难免有未尽之处,如有不妥,请随时联系删除。(文章内容仅供参考,具体效果以运行结果为准)

🌈4 Matlab代码、数据、文章
资料获取,更多粉丝福利,MATLAB|Simulink|Python资源获取





















 1307
1307

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








