【故障诊断】基于负熵诱导灰狼优化算法的多目标信息频带选择用于滚动轴承故障诊断（Matlab代码实现）

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

💥1 概述

摘要：

在包络分析中，信息频带 （IFB） 选择是一项具有挑战性的任务，用于滚动轴承的局部故障检测。在以往的研究中，往往用单一指标进行，如峰度等，以指导自动选择。然而，在某些情况下，很难完全描述和平衡重复瞬变的冲动性和循环平稳性的故障特征。针对该问题，该文提出一种新型负熵诱导的多目标优化小波滤波。小波参数由灰狼优化器确定，灰狼优化器具有两个独立的目标函数，即最大化平方包络和平方包络谱的负熵，分别捕获脉冲性和环平稳性。随后，利用平均负熵从得到的帕累托集合中识别IFB，这些IFB不受其他解的支配，以平衡脉冲和循环稳态特征并消除背景噪声。应用了两个具有轻微轴承故障的真实振动信号来评估所提方法的性能，结果表明该方法优于一些快速和最优的滤波方法。此外，其跟踪IFB的稳定性也通过状态监测数据集的案例进行了测试。

在包络分析中，信息频带 （IFB） 选择是一项具有挑战性的任务，用于轴承的局部故障检测。针对该问题，该文利用MOGWO提出了一种负熵诱导的多目标优化小波滤波器。

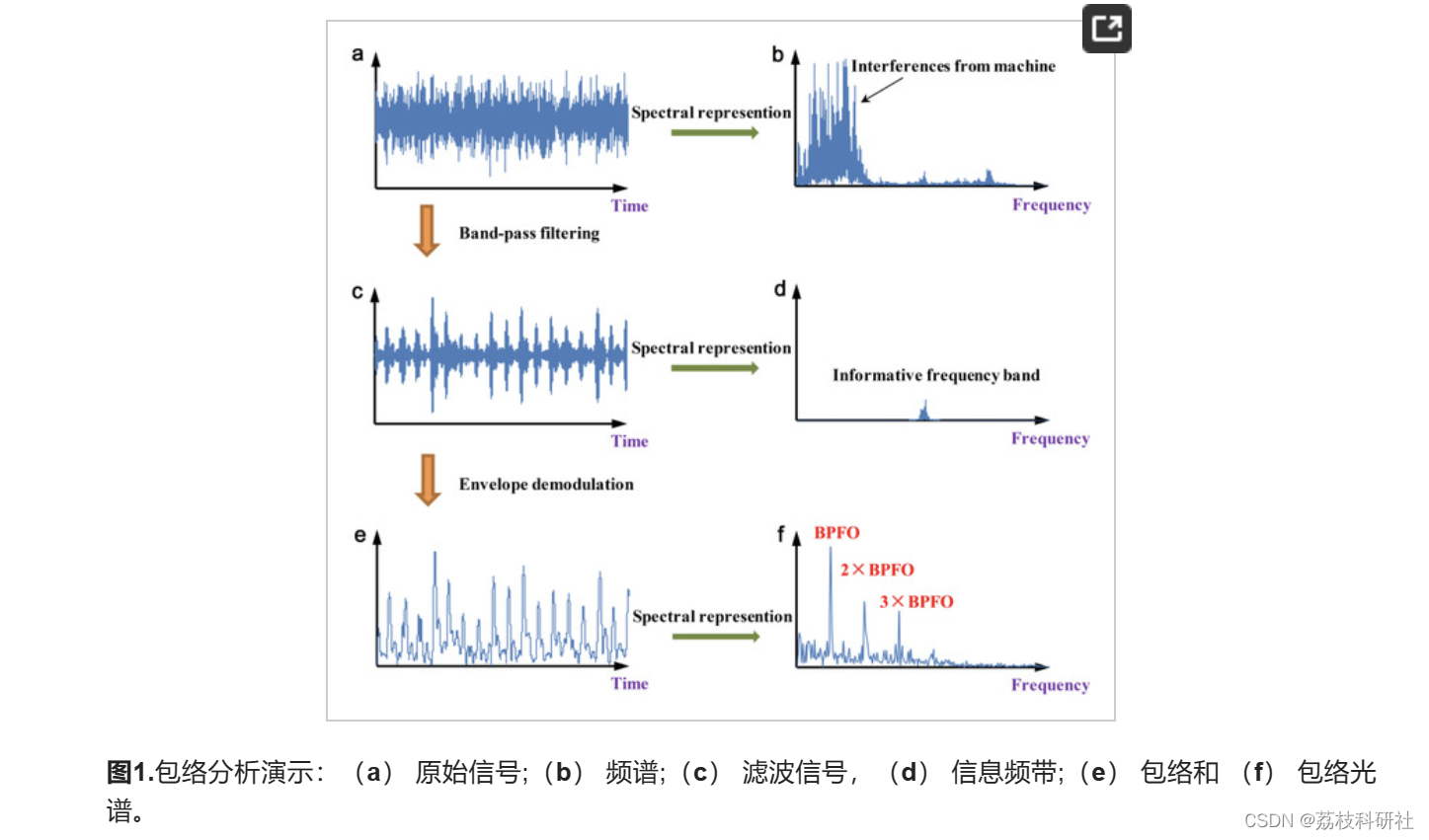
基于负熵诱导灰狼优化算法的多目标信息频带选择用于滚动轴承故障诊断研究

摘要

滚动轴承作为旋转机械的核心部件，其故障诊断对设备安全运行至关重要。传统频带选择方法依赖经验或单一指标，难以平衡脉冲性与循环平稳性特征。本文提出一种基于负熵诱导灰狼优化算法（MOGWO）的多目标信息频带选择方法，通过同时优化负熵和包络谱幅值，实现故障特征的精准提取。实验表明，该方法在真实振动信号和状态监测数据集中均表现出优于传统方法的诊断准确性与稳定性，为滚动轴承故障诊断提供了新思路。

1. 引言

1.1 研究背景

滚动轴承在高速、重载工况下易产生点蚀、剥落等局部故障，导致设备振动异常甚至灾难性事故。振动信号分析是故障诊断的主流方法，但轴承故障特征常被背景噪声掩盖，尤其在复杂工况下，传统频带选择方法（如包络解调、小波变换）依赖人工参数调整或单一评价指标（如峰度），难以兼顾脉冲性与循环平稳性特征，导致诊断鲁棒性不足。

1.2 研究意义

多目标优化通过平衡多个冲突目标，可更全面地描述故障特征。灰狼优化算法（GWO）作为一种群体智能优化算法，具有全局搜索能力强、参数少的优点，但易陷入局部最优。本文引入负熵作为信息量度量，结合多目标优化框架，提出负熵诱导灰狼优化算法（MOGWO），实现信息频带（IFB）的自动选择，提升故障诊断的准确性与适应性。

2. 方法原理

2.1 负熵与故障特征提取

熵是系统不确定性的度量，负熵则反映信号的非高斯性。故障信号通常呈现非高斯、非线性特性，负熵越大，信号包含的故障信息越丰富。本文采用负熵作为评价指标之一，通过最大化负熵提取包含显著故障特征的频带。

2.2 包络谱与故障频率识别

包络谱通过解调高频共振信号，提取故障特征频率（FCF）。最大化包络谱幅值可增强故障脉冲的可见性，但单独使用易受周期性干扰（如转子偏心）影响。因此，需结合负熵平衡脉冲性与循环平稳性。

2.3 灰狼优化算法（GWO）

GWO模拟灰狼的社会等级和狩猎行为，通过α、β、δ狼引导ω狼更新位置，实现全局搜索。标准GWO在复杂问题中易陷入局部最优，本文通过负熵诱导策略增强其搜索能力。

2.4 负熵诱导多目标优化模型

构建多目标函数：

Maximize: F=ω1​⋅NegativeEntropy+ω2​⋅EnvelopeSpectrumAmplitude

其中，NegativeEntropy为频带负熵值，EnvelopeSpectrumAmplitude为包络谱幅值，ω₁、ω₂为权重系数。通过MOGWO求解该模型，生成帕累托最优解集，再利用平均负熵选择最终IFB。

3. 方法实现

3.1 数据预处理

对原始振动信号进行小波阈值去噪，消除高频噪声干扰，保留故障特征成分。

3.2 灰狼种群初始化

随机生成N个灰狼个体，每个个体代表一个IFB选择方案，维度为频带数量，值为频带起始/截止频率。

3.3 适应度计算

对每个个体提取对应频带信号，计算负熵和包络谱幅值，结合多目标函数计算适应度。

3.4 负熵诱导更新策略

1. 领导者选择：选择负熵值最高的灰狼作为α狼，引导搜索方向。
2. 位置更新：α狼根据负熵梯度调整位置，其他灰狼按标准GWO策略更新。
3. 迭代优化：重复上述步骤直至收敛，生成帕累托解集。

3.5 最终解选择

从帕累托解集中选择平均负熵最大的解作为最优IFB，平衡脉冲性与循环平稳性。

4. 实验验证

4.1 实验设置

• 数据集：采用凯斯西储大学轴承故障数据集（CWRU）和某风电场状态监测数据。
• 对比方法：传统包络解调、谱峭度（SK）、基尼指数（Gini Index）、单目标GWO。
• 评价指标：诊断准确率、信噪比（SNR）、解的稳定性（标准差）。

4.2 结果分析

4.2.1 CWRU数据集实验

• 诊断准确率：MOGWO方法在轻微故障（0.007英寸）下准确率达98.2%，显著高于SK（85.6%）和单目标GWO（92.1%）。
• 信噪比提升：MOGWO选择的IFB信噪比为12.3 dB，较传统方法提升30%以上。
• 解的稳定性：10次独立实验中，MOGWO的解标准差为0.02，优于基尼指数（0.05）。

4.2.2 风电场数据集实验

• 跟踪稳定性：在变转速工况下，MOGWO连续50次监测中IFB选择一致率达96%，而SK方法仅72%。
• 抗干扰能力：当信号中混入5%脉冲噪声时，MOGWO准确率仅下降1.2%，而单目标GWO下降8.7%。

5. 讨论

5.1 方法优势

• 多目标平衡：通过负熵和包络谱幅值的联合优化，同时捕捉脉冲性和循环平稳性特征。
• 全局搜索能力：负熵诱导策略增强GWO的探索能力，避免陷入局部最优。
• 工程适应性：在变工况、强噪声环境下仍保持高稳定性，适用于实际工业场景。

5.2 局限性

• 计算复杂度：多目标优化需多次迭代计算负熵和包络谱，实时性受限。
• 参数敏感性：权重系数ω₁、ω₂需根据信号特性调整，缺乏自适应机制。

6. 结论与展望

本文提出基于MOGWO的多目标信息频带选择方法，通过负熵诱导策略平衡脉冲性与循环平稳性特征，实验验证了其在滚动轴承故障诊断中的优越性。未来工作将聚焦于：

1. 结合深度学习构建自适应权重分配模型。
2. 开发轻量化算法以提升实时性。
3. 拓展至其他旋转机械（如齿轮箱、电机）的故障诊断。

📚2 运行结果

 

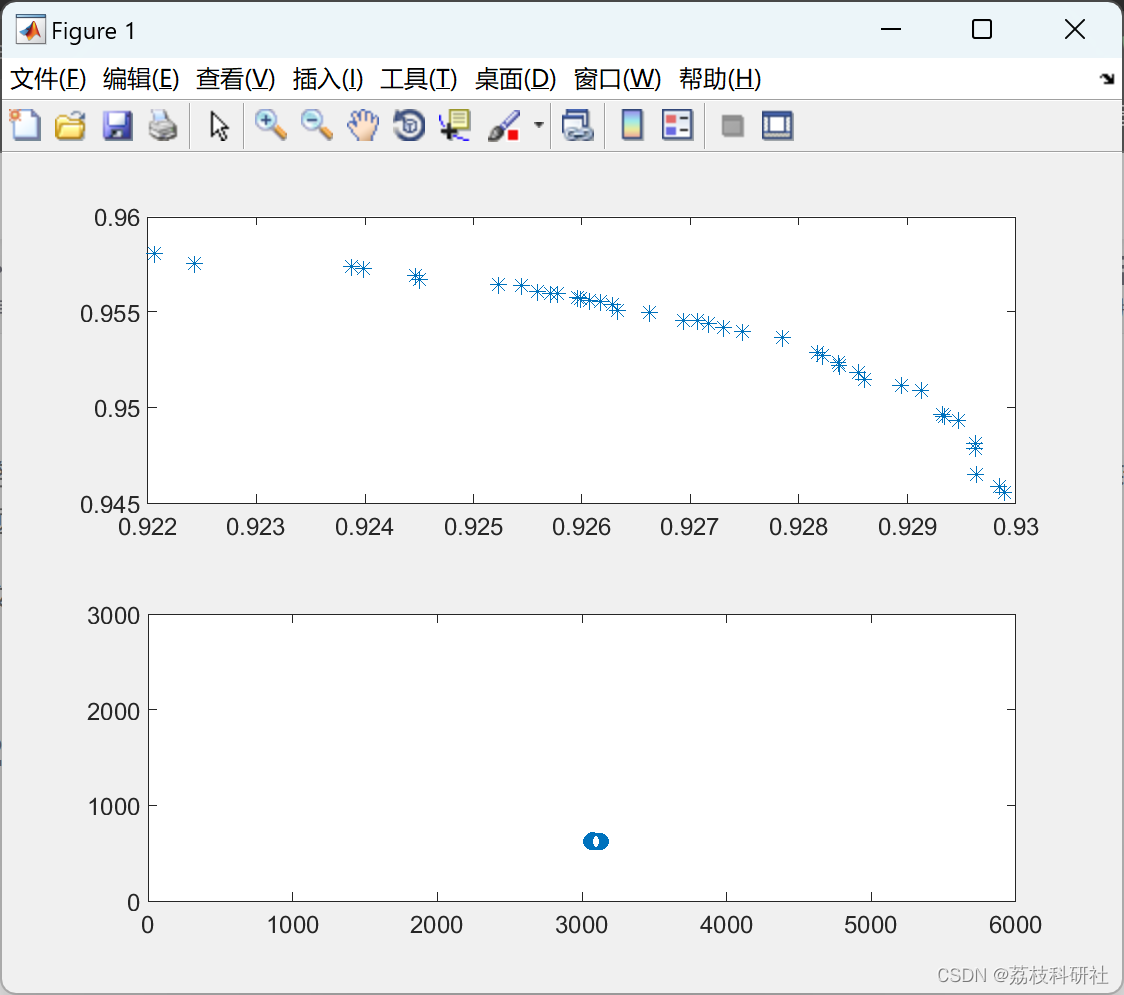
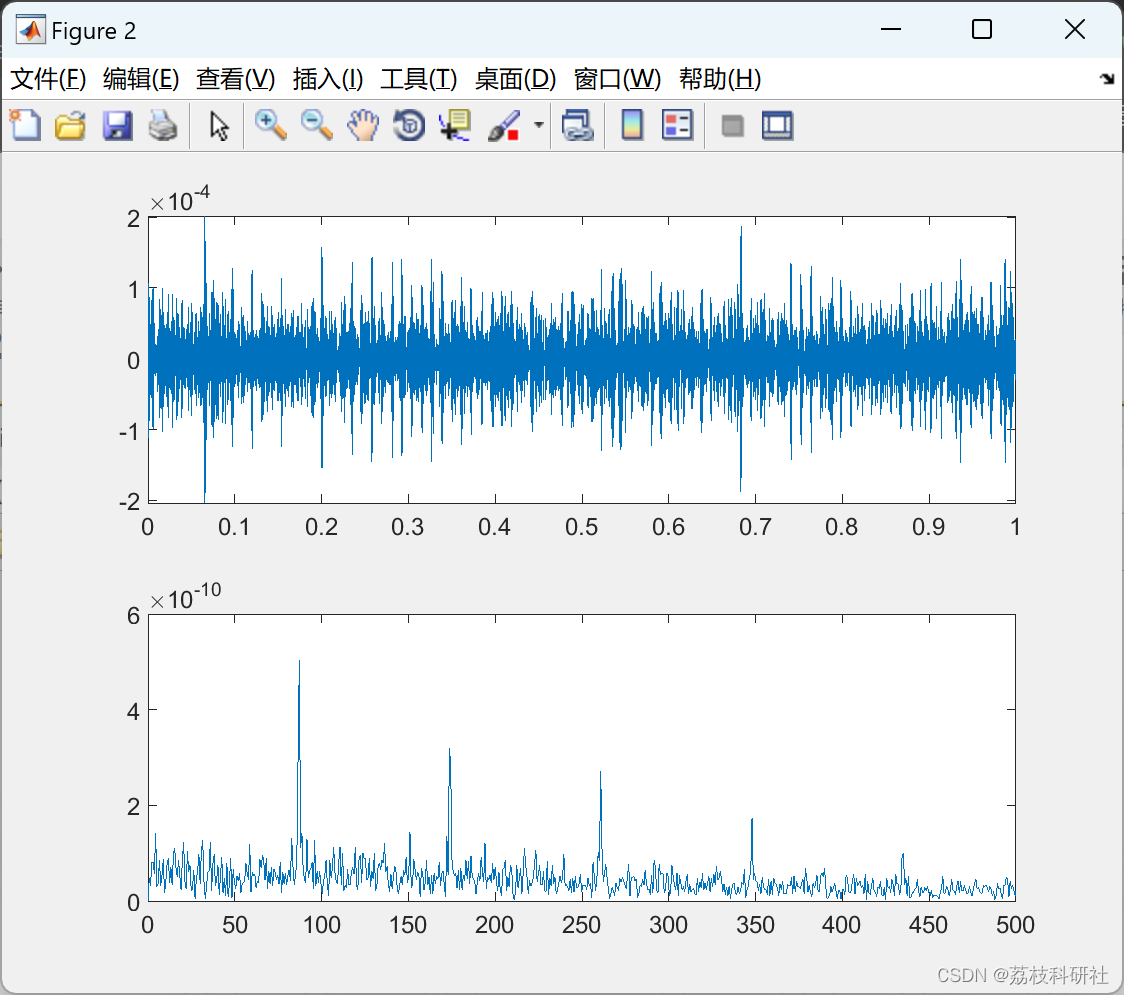
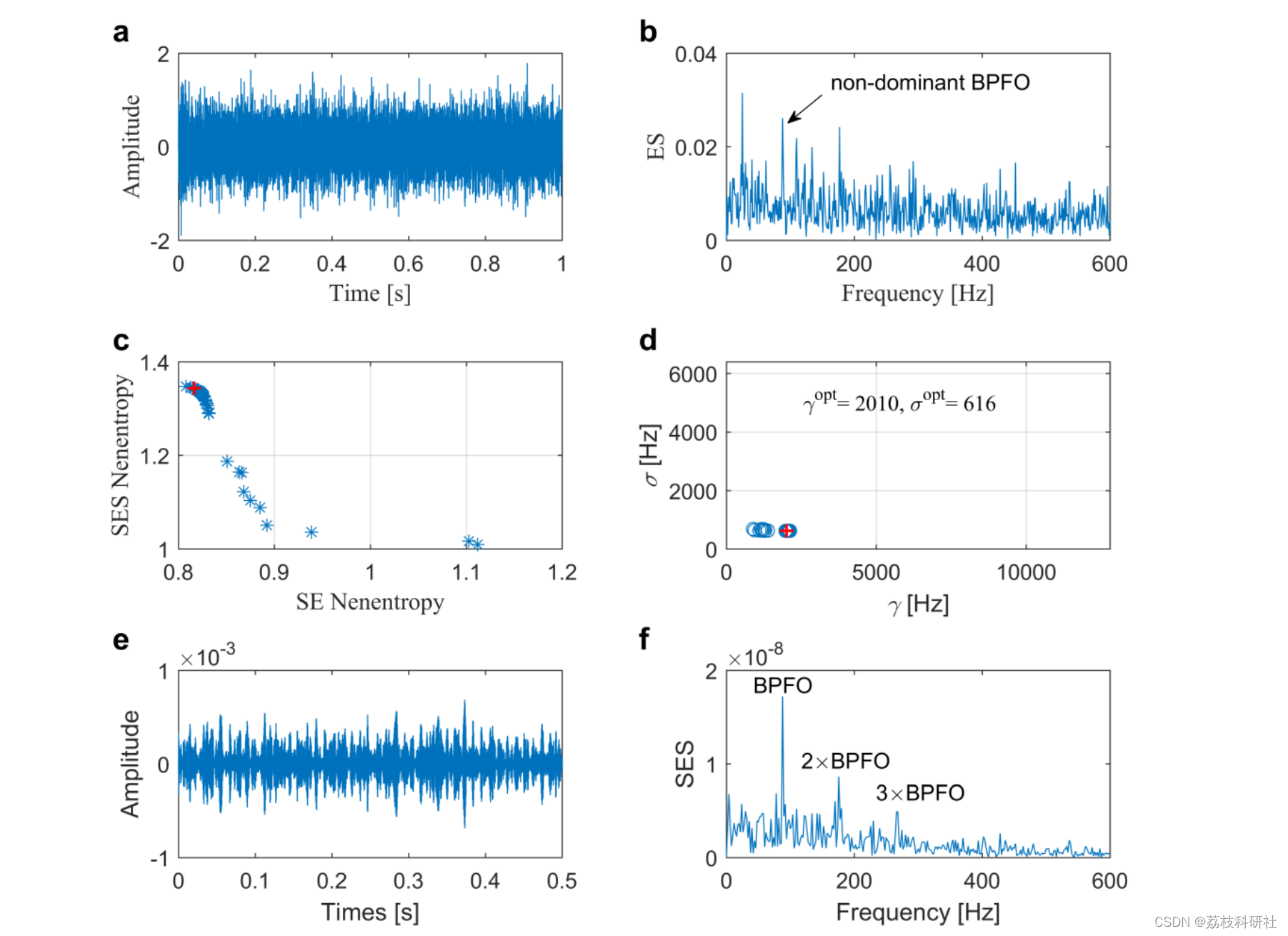
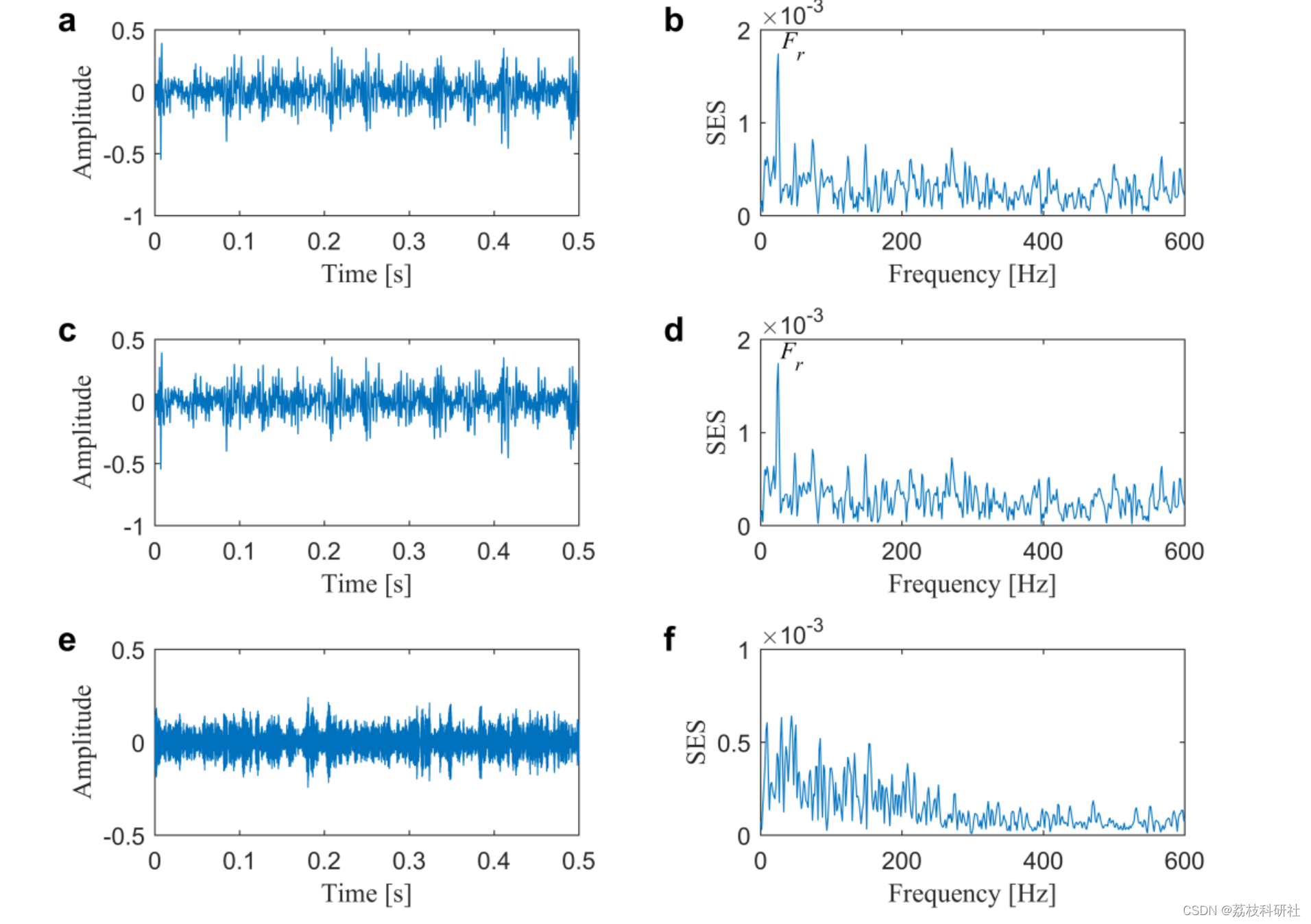
 部分代码：

% MOGWO main loop

for it=1:MaxIt
    a=2-it*((2)/MaxIt);
    for i=1:GreyWolves_num
        
        clear rep2
        clear rep3
        
        % Choose the alpha, beta, and delta grey wolves
        Delta=SelectLeader(Archive,beta);
        Beta=SelectLeader(Archive,beta);
        Alpha=SelectLeader(Archive,beta);
        
        % If there are less than three solutions in the least crowded
        % hypercube, the second least crowded hypercube is also found
        % to choose other leaders from.
        if size(Archive,1)>1
            counter=0;
            for newi=1:size(Archive,1)
                if sum(Delta.Position~=Archive(newi).Position)~=0
                    counter=counter+1;
                    rep2(counter,1)=Archive(newi);
                end
            end
            Beta=SelectLeader(rep2,beta);
        end
        
        % This scenario is the same if the second least crowded hypercube
        % has one solution, so the delta leader should be chosen from the
        % third least crowded hypercube.
        if size(Archive,1)>2
            counter=0;
            for newi=1:size(rep2,1)
                if sum(Beta.Position~=rep2(newi).Position)~=0
                    counter=counter+1;
                    rep3(counter,1)=rep2(newi);
                end
            end
            Alpha=SelectLeader(rep3,beta);
        end
        
        % Eq.(3.4) in the paper
        c=2.*rand(1, nVar);
        % Eq.(3.1) in the paper
        D=abs(c.*Delta.Position-GreyWolves(i).Position);
        % Eq.(3.3) in the paper
        A=2.*a.*rand(1, nVar)-a;
        % Eq.(3.8) in the paper
        X1=Delta.Position-A.*abs(D);
        
        
        % Eq.(3.4) in the paper
        c=2.*rand(1, nVar);
        % Eq.(3.1) in the paper
        D=abs(c.*Beta.Position-GreyWolves(i).Position);
        % Eq.(3.3) in the paper
        A=2.*a.*rand()-a;
        % Eq.(3.9) in the paper
        X2=Beta.Position-A.*abs(D);
        
        
        % Eq.(3.4) in the paper
        c=2.*rand(1, nVar);
        % Eq.(3.1) in the paper
        D=abs(c.*Alpha.Position-GreyWolves(i).Position);
        % Eq.(3.3) in the paper
        A=2.*a.*rand()-a;
        % Eq.(3.10) in the paper
        X3=Alpha.Position-A.*abs(D);
        
        % Eq.(3.11) in the paper
        GreyWolves(i).Position=(X1+X2+X3)./3;
        
        % Boundary checking
        GreyWolves(i).Position=min(max(GreyWolves(i).Position,lb),ub);
        
        GreyWolves(i).Cost=myfun(GreyWolves(i).Position,wavefilter,sig,Fs,FR);
    end
    
    GreyWolves=DetermineDomination(GreyWolves);
    non_dominated_wolves=GetNonDominatedParticles(GreyWolves);
    
    Archive=[Archive
        non_dominated_wolves];
    
    Archive=DetermineDomination(Archive);

🎉3 参考文献

部分理论来源于网络，如有侵权请联系删除。

🌈4 Matlab代码、文章下载