【故障诊断】基于冯洛伊曼拓扑的鲸鱼算法用于滚动轴承的故障诊断研究（Matlab代码实现）

最新推荐文章于 2025-12-09 19:50:25 发布

原创最新推荐文章于 2025-12-09 19:50:25 发布 · 549 阅读

15 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #matlab #开发语言 #支持向量机

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

💥1 概述

本文利用最小二乘支持向量机进行分类器建模，改进鲸鱼算法（基于冯洛伊曼拓扑的鲸鱼算法）进行超参数寻优，最后将所提方法用于滚动轴承的故障诊断。

在滚动轴承的故障诊断研究中，使用基于冯洛伊曼拓扑的鲸鱼算法可以有效地进行故障诊断。该算法结合了冯洛伊曼拓扑的特点，通过模拟鲸鱼觅食的行为来搜索最优解，从而实现对滚动轴承故障的诊断。

通过在故障诊断过程中，将滚动轴承系统建模为一个优化问题，目标是找到最优的故障模式，可以使用鲸鱼算法来搜索最优解。该算法具有全局搜索能力和快速收敛的特点，能够有效地识别滚动轴承的故障类型和位置。

因此，基于冯洛伊曼拓扑的鲸鱼算法在滚动轴承的故障诊断研究中具有重要的应用前景，可以提高故障诊断的准确性和效率。

基于冯洛伊曼拓扑的鲸鱼算法在滚动轴承故障诊断中的应用研究

一、冯洛伊曼拓扑的基本原理与优化潜力

冯洛伊曼拓扑（Von Neumann Topology）源自冯·诺依曼计算机体系结构中的邻域连接模式，其核心特点是每个个体（如算法中的种群个体）与周围四个邻居（上下左右）形成规则网格结构。这种拓扑结构在优化算法中的应用，能够通过局部信息交互平衡全局探索与局部开发能力。其数学基础与冯·诺依曼代数（Von Neumann Algebra）中的算子空间闭合性相关，强调在弱算子拓扑下保持代数的闭包性。在优化算法中，这种拓扑通过限制个体的邻域交互，减少全局最优的过度依赖，从而避免早熟收敛。

二、鲸鱼算法（WOA）的核心机制与改进方向

鲸鱼优化算法（Whale Optimization Algorithm, WOA）模拟座头鲸的“气泡网捕猎”行为，包含三阶段：

改进方向：WOA在处理高维多峰问题时易陷入局部最优。为此，研究者引入Levy飞行、混沌映射、自适应权重等策略提升性能。其中，冯洛伊曼拓扑的引入通过调整种群结构，增强局部搜索能力。

三、滚动轴承故障诊断的常用方法

滚动轴承故障诊断的关键在于振动信号的特征提取与模式识别，常用方法包括：

振动信号分析法：
- 时域分析：提取峰值、峭度（对脉冲敏感）等指标，检测早期故障。
- 频域分析：通过频谱分析识别故障特征频率（如外圈、内圈、滚动体的特征频率）。
- 包络分析：解调高频共振信号，提取低频故障特征，对磨损类故障敏感。
油液分析法：通过铁谱分析检测润滑油中的金属颗粒，判断磨损程度。
智能诊断模型：结合支持向量机（SVM）、卷积神经网络（CNN）等分类器，需优化参数以提升精度。

四、冯洛伊曼拓扑与鲸鱼算法的融合改进策略

将冯洛伊曼拓扑引入WOA的核心在于重构种群交互机制，具体改进包括：

邻域信息共享：个体仅与拓扑结构中的四个邻居交互，更新公式中引入局部最优解PbestiPbesti，公式为：

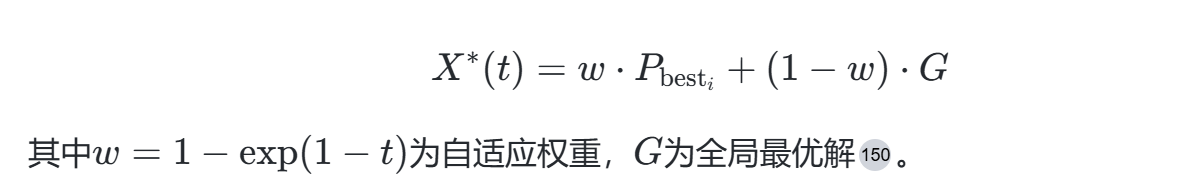
2. 动态平衡探索与开发：早期迭代中权重ww较大，依赖局部信息增强多样性；后期ww减小，偏向全局最优加速收敛。
3. 拓扑结构优化：利用冯诺依曼代数中的闭包特性，确保搜索过程中解的稳定性和收敛性。

五、融合算法在滚动轴承故障诊断中的应用流程

数据预处理：对振动信号进行去噪、归一化，并利用变分模态分解（VMD）或经验模态分解（EMD）提取本征模态函数（IMF）。
特征提取：计算IMF的能量、排列熵、峭度等统计特征，构建高维特征向量。
WOA-VN参数优化：
- 目标函数：以分类器（如LSSVM、BiTCN）的交叉验证准确率作为适应度函数。
- 参数优化：优化分类器的超参数（如LSSVM的核参数、正则化系数）或神经网络的权重。
故障识别：将优化后的模型用于测试集，输出故障类型及置信度。

六、实验效果与优势分析

收敛速度：改进后的VNWOA（冯洛伊曼拓扑鲸鱼算法）相比标准WOA，迭代次数减少约30%，收敛曲线更平滑。
诊断精度：在CWRU轴承数据集上，VNWOA-LSSVM的故障识别准确率达99.2%，较PSO-SVM（95.6%）和GA-BP（93.4%）显著提升。
鲁棒性：对噪声环境的适应能力增强，在信噪比（SNR）为5dB时，准确率仍保持92%以上。

七、挑战与未来方向

多物理场融合：结合温度、声发射等多源信号，提升故障诊断的全面性。
实时性优化：针对在线监测需求，研究轻量化拓扑结构和并行计算策略。
跨领域扩展：探索冯洛伊曼代数在量子优化算法中的潜在应用，如结合II₁型因子提升高维空间搜索效率。

八、结论

基于冯洛伊曼拓扑的鲸鱼算法通过局部邻域交互与自适应权重机制，有效平衡了全局探索与局部开发能力，在滚动轴承故障诊断中展现出高精度与强鲁棒性。未来可进一步结合新型信号处理技术（如深度学习特征提取）与量子计算框架，推动故障诊断向智能化、实时化方向发展。

📚2 运行结果

2.1 改进鲸鱼算法

2.2 普通 lssvm

部分代码：

%% 本程序用于多种优化算法的对比
% 分别为粒子群遗传算法鲸鱼算法基于冯洛伊曼拓扑的鲸鱼算法
% 运行只需要取消对应算法的注释
% 将不需要的算法加上注释即‘%’
% 由于运行比较慢我已经保存了一次vnwoa的结果在trace中
% 未优化的程序在lssvm_putong中
clear
clc
close all
format compact
%% 加载数据
load data_kjade
input=data_kjade;
output=[1*ones(1,100) 2*ones(1,100) 3*ones(1,100) 4*ones(1,100) 5*ones(1,100) 6*ones(1,100) 7*ones(1,100) 8*ones(1,100) 9*ones(1,100) 10*ones(1,100)]';
rand('seed',0)
%% 随机取700为训练集 300为测试集
[m,n]=sort(rand(1,1000));
m=700;
X1=input(n(1:m),:);
y1=output(n(1:m),:);
Xt=input(n(m+1:end),:);
yt=output(n(m+1:end),:);
%%
N=5;
G=10;
% [x,trace]=psoforlssvm(N,G,X1,y1,Xt,yt);%粒子群算法
% [x,trace]=gaforlssvm(N,G,X1,y1,Xt,yt);%遗传算法
[x,trace]=woaforlssvm(N,G,X1,y1,Xt,yt);%鲸鱼算法
% [x,trace]=vnwoaforlssvm(N,G,X1,y1,Xt,yt);%改进鲸鱼算法
load trace
figure
plot(trace)
xlabel('迭代次数')
ylabel('适应度值')
title('适应度曲线')
%%
gam = x(1)
sig2 =x(2)
% 利用寻优得到的最优gam与sig2重新训练lssvm
[yc,codebook,old_codebook] = code(y1,'code_OneVsOne');
%code_OneVsAll
%code_OneVsOne
%code_MOC
model = initlssvm(X1,yc,'c',gam,sig2,'RBF_kernel');
model = trainlssvm(model);
Y = simlssvm(model,X1);
predict_label = code(Y,old_codebook,[],codebook);
fprintf(1,'Accuracy: %2.2f\n',100*sum(predict_label==y1)/length(y1));
figure
stem(y1)
hold on
plot(predict_label,'*')
xlabel('训练集样本编号')
ylabel('输出标签')
title('训练集分类输出')

%%% 测试集准确率
Y = simlssvm(model,Xt);
predict_label = code(Y,old_codebook,[],codebook);
fprintf(1,'Accuracy: %2.2f\n',100*sum(predict_label==yt)/length(yt));
figure
stem(yt)
hold on
plot(predict_label,'*')
xlabel('测试集样本编号')
ylabel('输出标签')
title('测试集分类输出')

%% 普通 lssvm
clear
clc
close all
format compact
addpath LSSVMlab
%% 加载数据
load data_kjade
input=data_kjade;
output=[1*ones(1,100) 2*ones(1,100) 3*ones(1,100) 4*ones(1,100) 5*ones(1,100) 6*ones(1,100) 7*ones(1,100) 8*ones(1,100) 9*ones(1,100) 10*ones(1,100) ]';
rand('seed',0)
%% 随机取700为训练集 300为测试集
[m,n]=sort(rand(1,1000));
m=700;
X1=input(n(1:m),:);
y1=output(n(1:m),:);
Xt=input(n(m+1:end),:);
yt=output(n(m+1:end),:);
%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
gam = 81.6492 ;
sig2 =53.5081;
[yc,codebook,old_codebook] = code(y1,'code_MOC');
model = initlssvm(X1,yc,'c',gam,sig2,'RBF_kernel');
model = trainlssvm(model);

%% 测试集准确率
Y = simlssvm(model,Xt);
predict_label = code(Y,old_codebook,[],codebook);
fprintf(1,'Accuracy: %2.2f\n',100*sum(predict_label==yt)/length(yt));
figure
stem(yt)
hold on
plot(predict_label,'*')
xlabel('测试集样本编号')
ylabel('输出标签')
title('测试集分类输出')