💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
⛳️赠与读者
👨💻做科研,涉及到一个深在的思想系统,需要科研者逻辑缜密,踏实认真,但是不能只是努力,很多时候借力比努力更重要,然后还要有仰望星空的创新点和启发点。建议读者按目录次序逐一浏览,免得骤然跌入幽暗的迷宫找不到来时的路,它不足为你揭示全部问题的答案,但若能解答你胸中升起的一朵朵疑云,也未尝不会酿成晚霞斑斓的别一番景致,万一它给你带来了一场精神世界的苦雨,那就借机洗刷一下原来存放在那儿的“躺平”上的尘埃吧。
或许,雨过云收,神驰的天地更清朗.......🔎🔎🔎
💥1 概述

一、研究背景与意义
BP神经网络因其强大的非线性拟合能力被广泛应用于预测任务,但存在易陷入局部极小值、收敛速度慢、初始权值敏感等缺陷 [[8-9, 13]]。模拟退火算法(Simulated Annealing, SA)作为一种全局优化算法,通过概率性接受劣解的机制跳出局部最优,与BP神经网络结合可显著提升模型鲁棒性和预测精度 。该混合模型(SA-BP)已在遥感、电力负荷预测、机械故障诊断等领域验证有效性 。
二、基础理论
1. BP神经网络结构
- 三层典型结构:输入层、隐含层(≥1层)、输出层,层间全连接 。
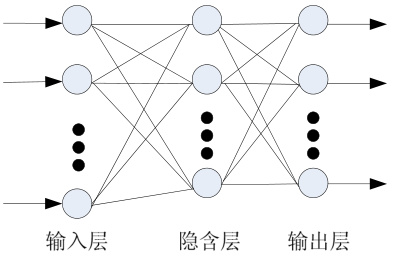
- 训练机制:
- 前向传播:输入数据经加权和与激活函数(如Sigmoid、ReLU)逐层传递至输出层 。
- 反向传播:根据输出误差(如均方误差MSE),通过梯度下降法调整权值和阈值 。
2. 模拟退火算法原理
- 物理隐喻:模拟金属退火过程,通过温度参数控制搜索过程的随机性 。
- 核心步骤:
- 产生新解:在当前位置随机扰动生成新解。
- Metropolis准则:若新解更优(ΔE < 0)则接受;否则以概率 <code>P = exp(-ΔE / T)</code> 接受 。
- 降温策略:温度按指数衰减(<code>T' = T × d</code>,d ∈ [0.8, 0.99])直至终止温度 。
三、SA-BP模型优化机制
1. 优化目标
- 解决BP缺陷:SA的全局搜索能力可避免BP陷入局部极小值 。
- 优化对象:SA优化BP的初始权值与阈值,替代随机初始化 。
2. 算法流程
SA-BP模型构建分为六步 :
- 参数初始化:
- SA参数:初始温度(<code>T<sub>max</sub> = 100</code>)、终止温度(<code>T<sub>min</sub> = 0.01</code>)、降温系数(<code>d = 0.95</code>)、迭代次数(<code>L = 150</code>)。
- BP参数:网络层数、节点数、目标误差(如0.001)、学习率(如0.001)。
- 随机生成初始解:BP的权值向量作为SA的初始状态。
- 迭代优化:
- 产生新权值解:在当前权值附近随机扰动。
- 计算能量差:<code>Δt = E(S') - E(S)</code>(E为BP的预测误差函数)。
- 按Metropolis准则接受新解。
- 降温更新:<code>T = T × d</code>。
- 终止条件:连续多次无新解被接受或达到<code>T<sub>min</sub></code>。
- 输出最优权值训练BP网络。
关键优势:SA在高温阶段接受劣解,扩大搜索范围;低温阶段聚焦局部精细搜索,平衡全局与局部优化 。
四、参数设置与实验设计
1. 参数设置经验
| 参数类型 | 建议值/范围 | 依据 |
|---|---|---|
| 初始温度(T<sub>max</sub>) | 100–1000 | 覆盖足够大的解空间 |
| 终止温度(T<sub>min</sub>) | 0.01–0.001 | 确保收敛稳定性 |
| 降温系数(d) | 0.85–0.99 | 平衡收敛速度与精度 |
| 权值范围 | [-3, 3] | 避免梯度爆炸 |
| BP隐含层节点数 | √(输入节点+输出节点) + 5 | 经验公式 |
2. 典型实验流程
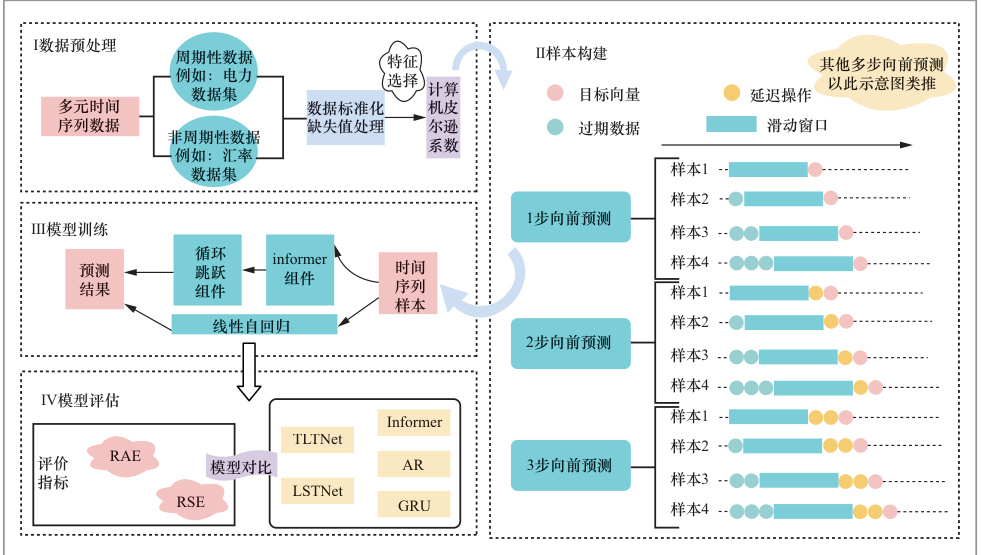
- 数据预处理:归一化、缺失值填补、特征选择(如PCA降维 )。
- 样本划分:训练集(70%)、验证集(15%)、测试集(15%)。
- 模型训练:
- SA优化BP权值(全局搜索)。
- BP微调(局部收敛)。
- 预测与评估:对比SA-BP、BP、其他优化模型(如GA-BP、PSO-BP)。
五、性能评估与案例分析
1. 评估指标
| 指标 | 公式 | 适用场景 |
|---|---|---|
| MAE | Σ|预测值-真实值|/n | 对异常值不敏感 |
| RMSE | (Σ(预测值-真实值)²/n) | 惩罚大误差,单位一致性 |
| R² | 模型解释方差比例 | 拟合优度 |
2. 应用案例效果
- GPS高程拟合:GSA-BP(SA+GA优化BP)比BP精度提升51%,速度提升77% 。
- 叶面积指数预测:SA-BP的RMSE比传统BP降低20%,有效克服局部最优 。
- 船舶油耗预测:SA-BP的R²达0.92,优于PSO-BP和GA-BP 。
六、挑战与改进方向
- 计算效率:SA的多次迭代导致训练时间长,可结合并行计算或自适应降温策略加速 。
- 参数敏感性:SA参数(d、T)需针对任务调优,建议采用网格搜索或元启发式算法二次优化 。
- 混合策略:SA与GA、PSO等结合(如GSA-BP),兼顾全局搜索与收敛速度 。
结论
模拟退火算法优化BP神经网络通过融合全局优化与局部微调,显著提升了预测模型的鲁棒性和精度。其在参数优化机制(如Metropolis准则接受劣解)、实验设计流程(数据预处理→SA权值优化→BP训练)及评估指标(RMSE、R²)方面已形成标准化框架。未来研究可聚焦自适应参数调整与多算法协同优化,进一步拓展其在复杂系统预测中的应用深度。
📚2 运行结果

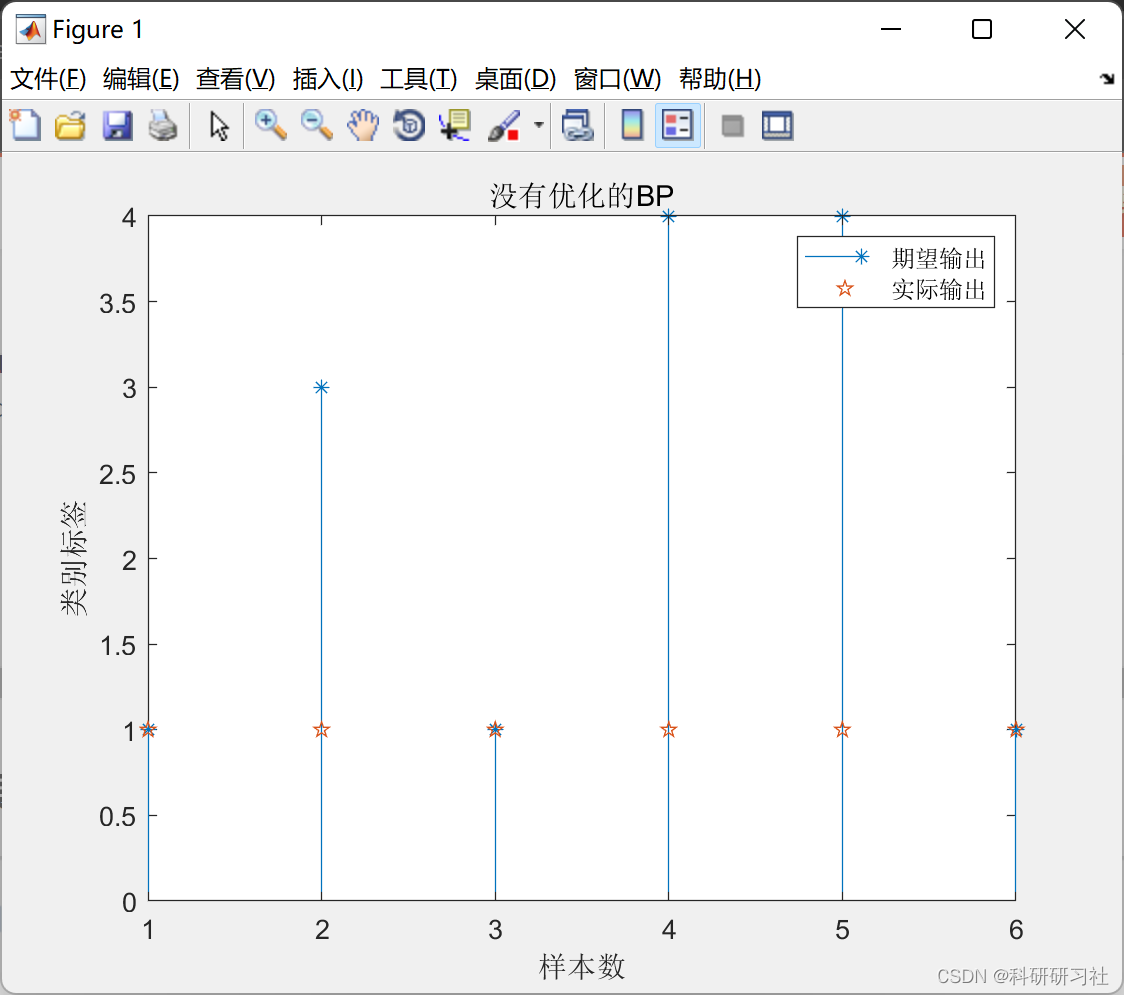
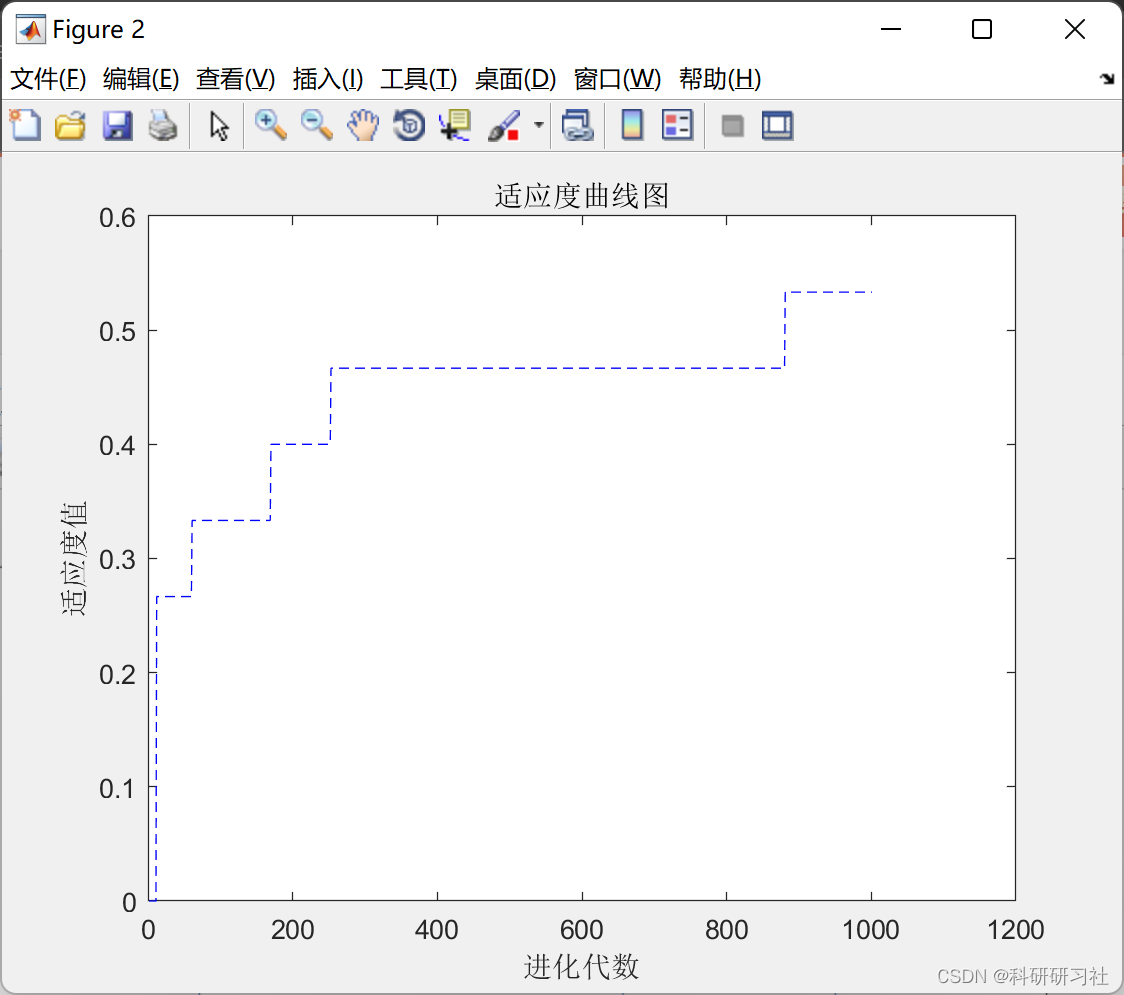
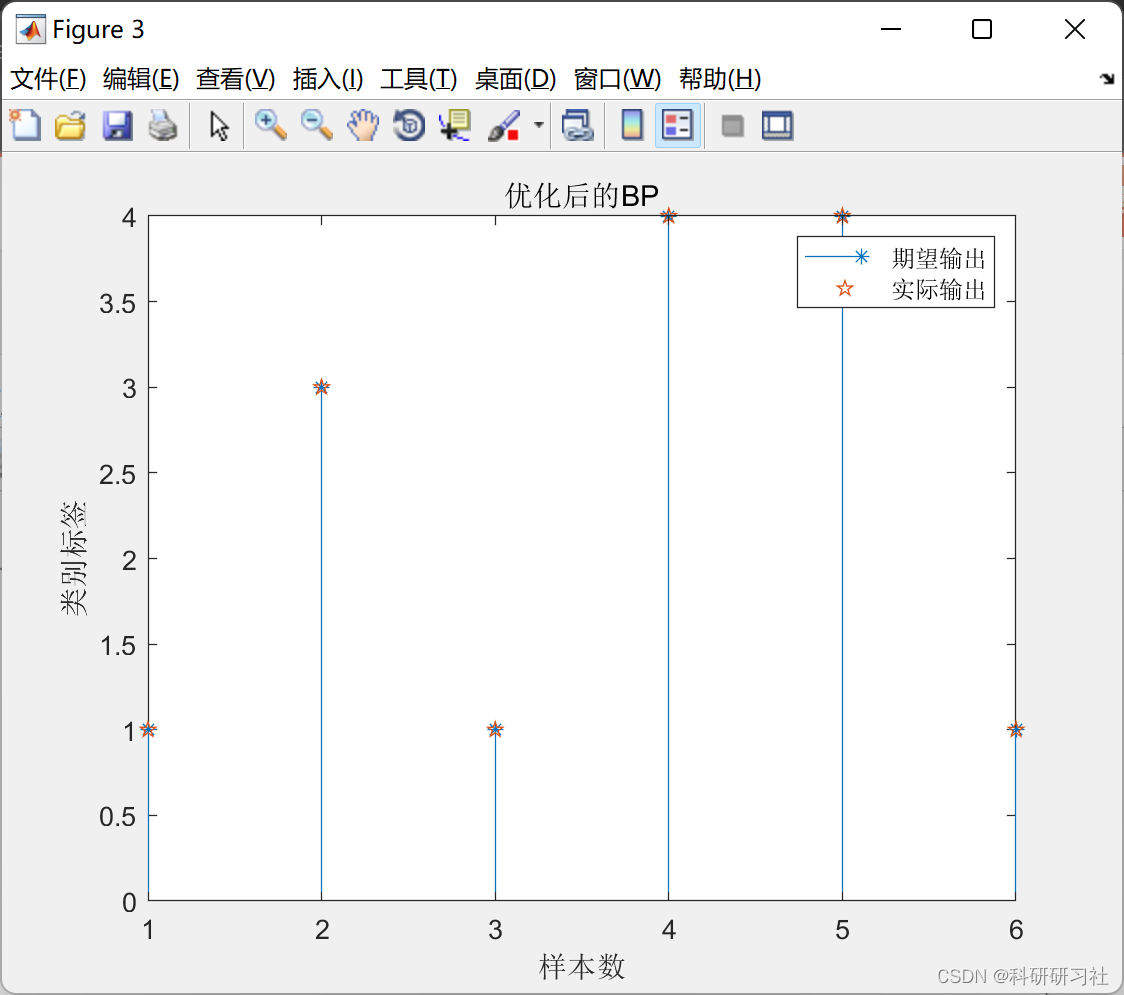
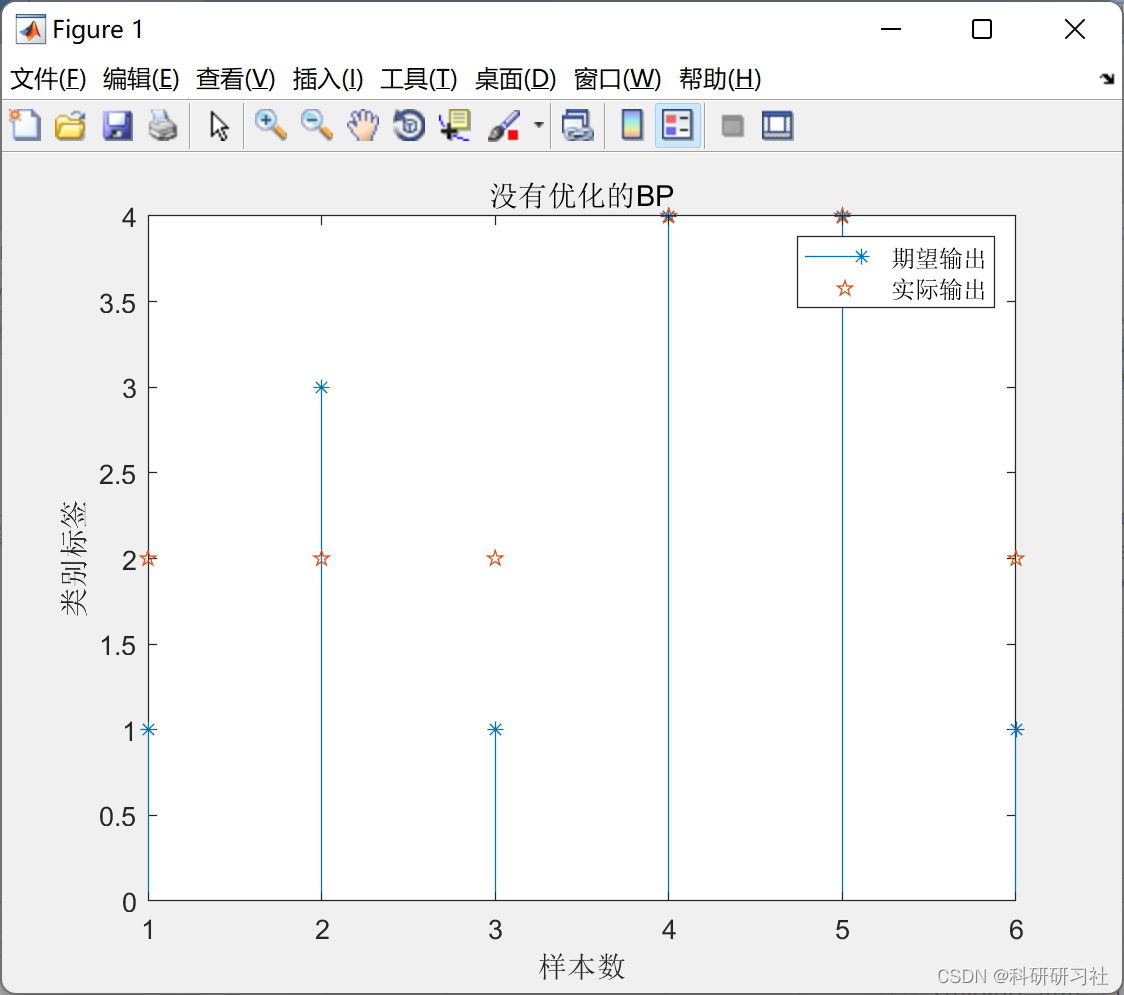
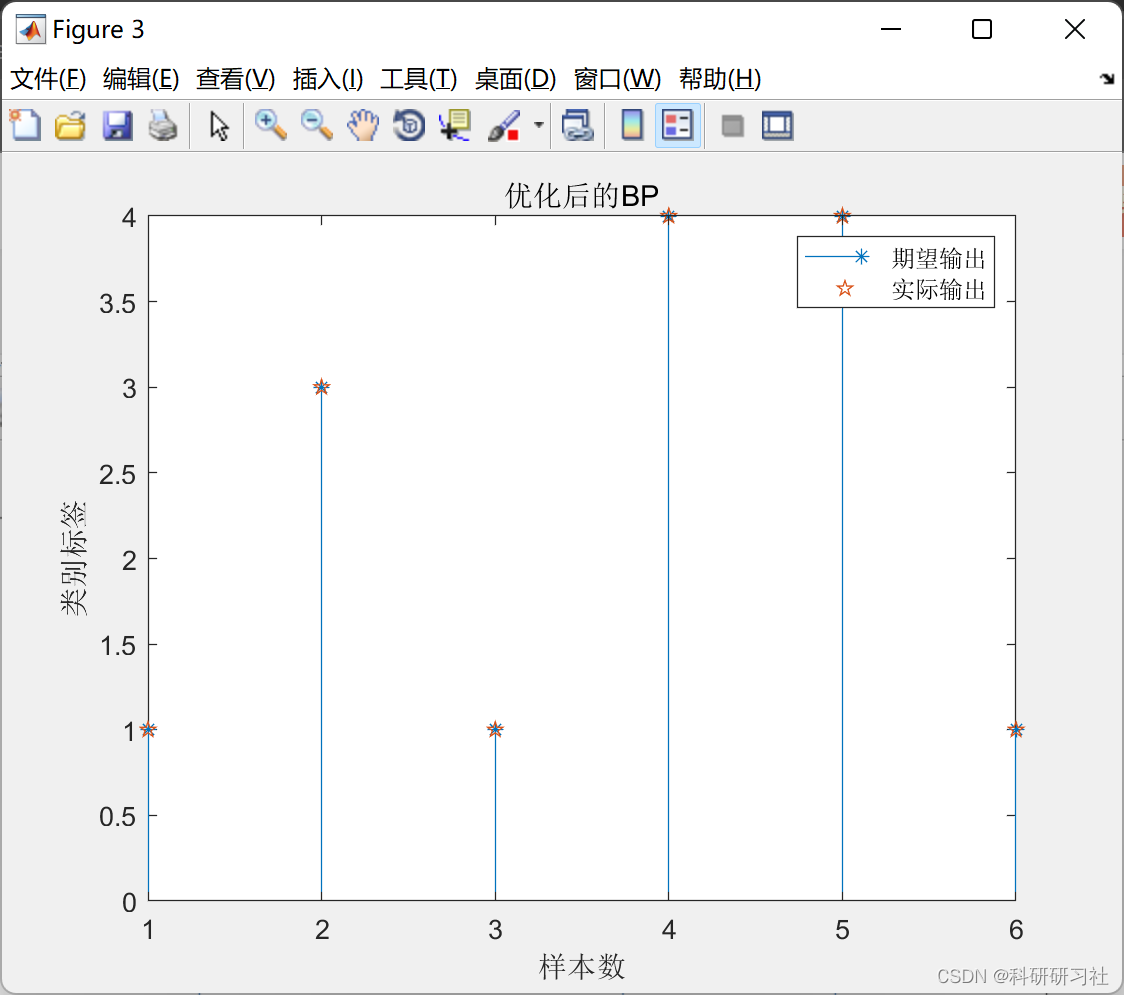
部分代码:
function [h,trace]=saforbp(inputnum,hiddennum,outputnum,inputn_train,label_train,net)
%% 参数设定
%%%冷却表参数%%%%%%%%%%
L=10; %马尔科夫链长度
K=0.9; %衰减因子
S=0.01; %步长因子
T=100; %初始温度
P=0; %Metroppolis过程中总接受点
max_iter=100;%最大退火次数
%% 随机产生10个初始值,并从10个初值中产生1个处置最优解
Xs=1;
Xx=0;
pop=20;
D=inputnum*hiddennum+hiddennum+hiddennum*outputnum+outputnum;
Prex=(rand(D,pop)*(Xs-Xx)+Xx);
for i=1:pop
funt(i)=fun(Prex(:,i)',inputnum,hiddennum,outputnum,inputn_train,label_train,net);
end
[sort_val,index_val] = sort(funt,'descend');
Prebestx=Prex(:,index_val(end));
Prex=Prex(:,index_val(end-1));
Bestx=Prex;
bestfit=zeros(1,max_iter);
%每迭代一次退火一次(降温),直到满足迭代条件为止
for iter=1:max_iter
iter
T=K*T;%在当前温度T下迭代次数
for i=1:L
%在附近随机选下一点
Nextx=Prex+S*(rand(D,1)*(Xs-Xx)+Xx);
%边界条件处理
for ii=1:D
if Nextx(ii)>Xs | Nextx(ii)<Xx
Nextx(ii)=rand*(Xs-Xx)+Xx;
end
end
%%是否全局最优解
a=fun(Bestx',inputnum,hiddennum,outputnum,inputn_train,label_train,net);
b=fun(Nextx',inputnum,hiddennum,outputnum,inputn_train,label_train,net);
if a<b
prebest=a;
Prebestx=Bestx;%保留上一个最优解
Bestx=Nextx;%更新最优解
a=b;
end%如果新解更好,用新解替代最优解,原最优解变为前最优解
%%%%%%%%%%%%Metropolis过程
c=fun(Prex',inputnum,hiddennum,outputnum,inputn_train,label_train,net);
if c<b
%%%接受新解
Prex=Nextx;
P=P+1;
else
changer=-1*(b-c)/T;
p1=exp(changer);
%%%以一定概率接受较差的解
if p1>rand
Prex=Nextx;
P=P+1;
end
end
trace(P+1)=a;
end
end
h=Bestx';
end
%
🎉3 参考文献
文章中一些内容引自网络,会注明出处或引用为参考文献,难免有未尽之处,如有不妥,请随时联系删除。(文章内容仅供参考,具体效果以运行结果为准)
[1]蒋美云.基于模拟退火算法优化的BP神经网络预测模型[J].软件工程,2018,21(07):36-38.
🌈4 Matlab代码实现
资料获取,更多粉丝福利,MATLAB|Simulink|Python资源获取





















 910
910

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








