💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
蜂群无人机时间与角度约束下的协同攻击算法研究
摘要
随着无人机技术的快速发展,多无人机协同攻击成为研究热点。本文聚焦蜂群无人机在时间与角度约束下的协同攻击算法,提出一种基于虚拟引导点结合人工势场法和模型预测控制(MPC)的协同攻击策略。该策略通过引入虚拟引导点引导无人机运动,利用人工势场法设计路径规划,并采用MPC控制器实现对飞行时间和攻击角度的精确约束。仿真结果表明,该算法能有效协调多架无人机协同攻击,满足时间和角度约束,具有较高的可行性和实用性。
关键词
蜂群无人机;协同攻击;虚拟引导点;人工势场法;模型预测控制;飞行时间约束;攻击角度约束
1. 引言
1.1 研究背景与意义
无人机技术近年来取得显著进步,在军事、民用领域广泛应用。多无人机协同攻击技术凭借灵活性、机动性和安全性优势,成为研究焦点。蜂群无人机作为多无人机系统的一种,通过大量无人机协同作战,可实现对目标的精确打击。在协同攻击中,飞行时间和攻击角度是关键因素,直接影响攻击效果和任务成功率。因此,研究时间与角度约束下的协同攻击算法具有重要意义。
1.2 国内外研究现状
- 国外研究:美国等军事强国在蜂群无人机协同攻击领域投入大量资源,开展多项研究项目。例如,美国国防预先研究计划局(DARPA)推出“小精灵”项目,研发可空中回收的无人机蜂群,用于侦察、电子战等任务;美国防部战略能力办公室(SCO)启动“无人机蜂群”项目,通过有人机空射“灰山鹑”微型无人机蜂群,执行低空态势感知和干扰任务。这些项目在协同感知、决策、编队飞行和任务分配等方面取得一定成果,为协同攻击算法研究提供技术基础。
- 国内研究:国内也积极开展相关研究,中国电科(CETC)电子科学研究院发布陆军协同无人机“蜂群”视频,展示无人机蜂群协同作战能力。同时,国内学者在协同攻击算法方面提出多种方法,如基于行为的协同攻击、基于路径规划的协同攻击和基于优化理论的协同攻击等,但这些方法在应对复杂环境和动态目标时存在一定局限性。
1.3 研究目的与内容
本文旨在研究蜂群无人机在时间与角度约束下的协同攻击算法,提出一种有效协调多架无人机协同攻击的策略。研究内容包括:引入虚拟引导点引导无人机运动;利用人工势场法设计无人机路径规划;采用MPC控制器实现对飞行时间和攻击角度的精确约束;通过仿真实验验证算法的有效性和可行性。
2. 相关技术与理论基础
2.1 蜂群无人机技术概述
蜂群无人机由大量小型、低成本无人机组成,通过先进通信技术实现信息共享和实时交互。它们依据预设规则或智能算法协同行动,具有高度智能化和自主性。在协同攻击中,蜂群无人机可发挥数量优势,从多方向对目标实施饱和攻击,提高打击效果。
2.2 协同攻击关键技术
- 协同感知与决策:蜂群无人机通过传感器获取战场环境信息,利用信息共享和实时通信实现对战场态势的全面了解。基于人工智能和机器学习技术,无人机可自主决策,根据任务需求和战场环境制定最优作战方案。
- 协同编队与飞行控制:为保持作战行动的协调性和一致性,蜂群无人机需进行紧密编队飞行。研究人员开发多种协同编队算法,如基于规则的方法、基于优化的方法和基于学习的方法等,实时调整编队队形和飞行轨迹,确保无人机在复杂战场环境中保持高度协同作战能力。
- 任务分配:任务分配是协同攻击的关键环节,直接影响攻击效果和任务成功率。常见任务分配算法包括集中式任务分配和分布式任务分配。集中式任务分配由中央控制器负责全局任务分配,具有较强的自适应性和鲁棒性;分布式任务分配则由各无人机根据局部信息进行自主任务分配,具有更好的适应性和灵活性。
2.3 人工势场法
人工势场法是一种常用的路径规划算法,通过构建目标引力场和障碍物斥力场,引导无人机避开障碍物并朝向目标运动。在协同攻击中,人工势场法可为每架无人机规划路径,确保无人机在飞行过程中避开障碍物和其他无人机,同时朝向目标运动。
2.4 模型预测控制(MPC)
MPC是一种基于模型的控制方法,利用系统预测模型预测未来状态,并根据预测结果计算控制信号,实现对系统的控制。在协同攻击中,MPC控制器可利用无人机动力学模型,预测无人机未来状态,并计算控制信号,确保无人机在指定时间内到达目标攻击区域,并保持一定的攻击角度。
3. 基于虚拟引导点的协同攻击策略
3.1 虚拟引导点引入
为协调多架无人机协同攻击,引入虚拟引导点作为无人机运动的引导目标。虚拟引导点位于目标攻击区域内,以特定速度运动。所有无人机均以虚拟引导点为目标进行运动,实现协同攻击。
3.2 人工势场法路径规划
在多无人机协同攻击中,采用人工势场法为每架无人机规划路径。具体包括:
- 目标吸引力:指向目标方向,大小与无人机到目标的距离成反比。
- 虚拟引导点吸引力:指向虚拟引导点方向,大小与无人机到虚拟引导点的距离成反比。
- 障碍物排斥力:指向远离障碍物方向,大小与无人机到障碍物的距离成反比。
通过综合计算这些力,确定无人机的运动方向,实现路径规划。
3.3 MPC控制器设计
为实现飞行时间和攻击角度的精确约束,采用MPC控制器进行控制。MPC控制器利用无人机动力学模型,预测无人机未来状态,并计算控制信号。具体步骤如下:
- 建立无人机动力学模型:考虑无人机的运动学和动力学特性,建立准确的动力学模型。
- 预测未来状态:根据当前状态和动力学模型,预测无人机在未来一段时间内的状态。
- 计算控制信号:根据预测结果和约束条件(如飞行时间和攻击角度),计算最优控制信号,确保无人机在指定时间内到达目标攻击区域,并保持一定的攻击角度。
4. 仿真实验与结果分析
4.1 仿真环境搭建
利用Matlab/Simulink搭建仿真环境,模拟蜂群无人机协同攻击场景。仿真环境中包括目标、障碍物和无人机等元素,设置不同的飞行时间和攻击角度约束条件,验证算法的有效性和可行性。
4.2 仿真参数设置
设置无人机数量、初始位置、速度、目标位置、障碍物位置等参数。同时,设置飞行时间约束和攻击角度约束条件,如飞行时间不超过T秒,攻击角度在θ范围内等。
4.3 仿真结果分析
- 协同攻击效果:仿真结果表明,引入虚拟引导点结合人工势场法和MPC控制器的协同攻击策略能有效协调多架无人机协同攻击。无人机能够按照预设路径飞行,并在指定时间内到达目标攻击区域,同时保持一定的攻击角度。
- 约束条件满足情况:通过对比实际飞行时间和攻击角度与约束条件,发现算法能够满足飞行时间和攻击角度的精确约束要求。在多数仿真实验中,实际飞行时间与预设飞行时间的误差在允许范围内,攻击角度也保持在预设范围内。
- 鲁棒性分析:为验证算法的鲁棒性,在仿真环境中引入随机干扰因素,如风速变化、传感器噪声等。仿真结果表明,算法在存在干扰因素的情况下仍能保持较好的协同攻击效果,满足约束条件要求,具有一定的鲁棒性。
5. 结论与展望
5.1 研究成果总结
本文提出一种基于虚拟引导点结合人工势场法和MPC控制的蜂群无人机协同攻击策略。该策略通过引入虚拟引导点引导无人机运动,利用人工势场法设计路径规划,并采用MPC控制器实现对飞行时间和攻击角度的精确约束。仿真实验结果表明,该算法能有效协调多架无人机协同攻击,满足时间和角度约束要求,具有较高的可行性和实用性。
5.2 研究不足与改进方向
尽管本文研究取得一定成果,但仍存在一些不足之处。例如,在复杂环境下,算法的实时性和计算效率可能受到影响;在应对动态目标时,算法的适应性和灵活性有待提高。未来研究可从以下方面进行改进:
- 优化算法实时性:研究更高效的算法实现方式,提高算法的实时性和计算效率,以适应复杂环境下的协同攻击需求。
- 增强算法适应性:考虑动态目标的变化情况,研究更适应动态目标的协同攻击算法,提高算法的适应性和灵活性。
- 结合其他技术:将协同攻击算法与其他技术(如机器学习、深度学习等)相结合,进一步提高算法的智能化水平和协同攻击效果。
5.3 应用前景展望
随着无人机技术的不断发展和应用领域的拓展,蜂群无人机协同攻击算法在军事、民用等领域具有广阔的应用前景。在军事领域,该算法可用于侦察、打击、电子战等多种任务,提高作战效能和战场生存能力;在民用领域,该算法可用于物流配送、环境监测、灾害救援等任务,提高作业效率和安全性。未来,随着技术的不断进步和创新,蜂群无人机协同攻击算法将迎来更广阔的发展空间。
📚2 运行结果
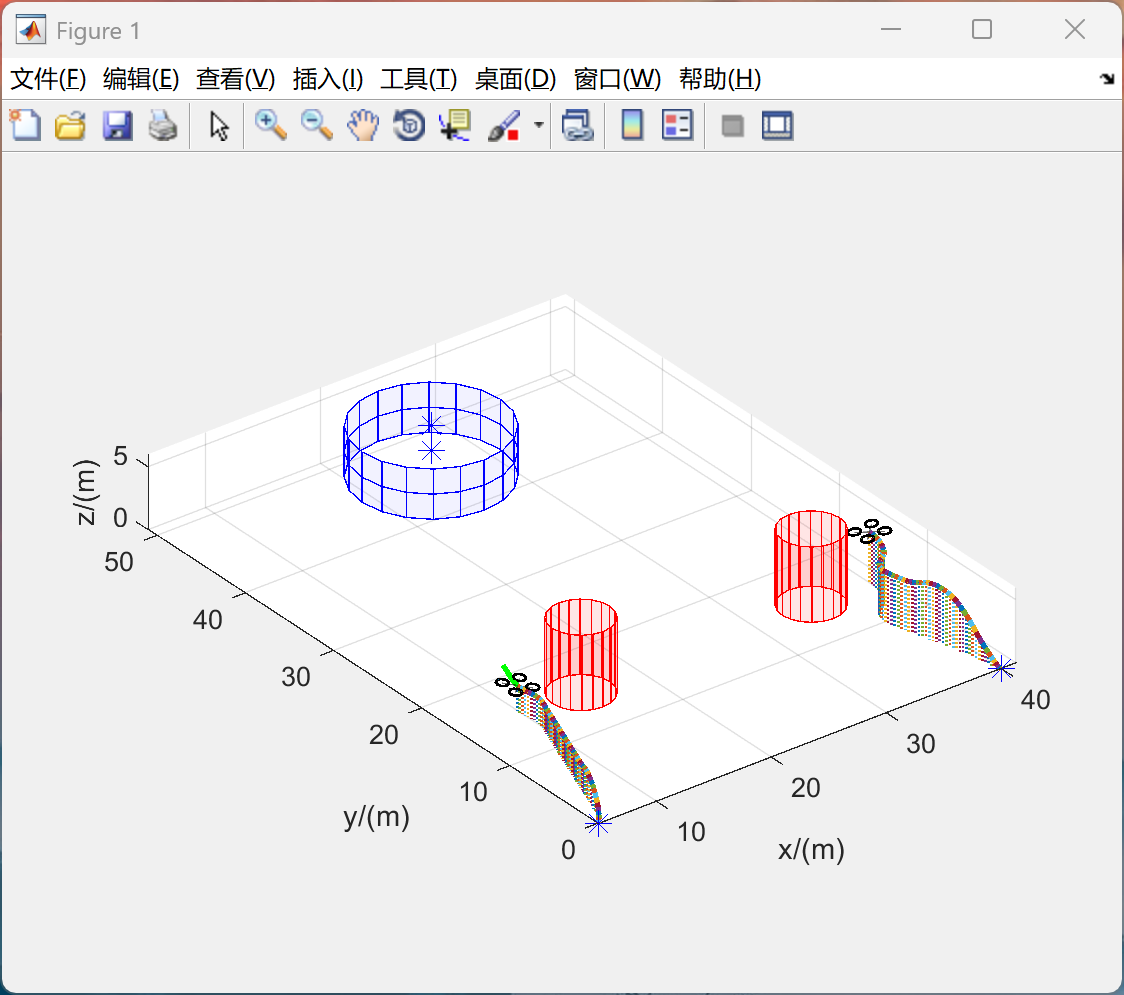
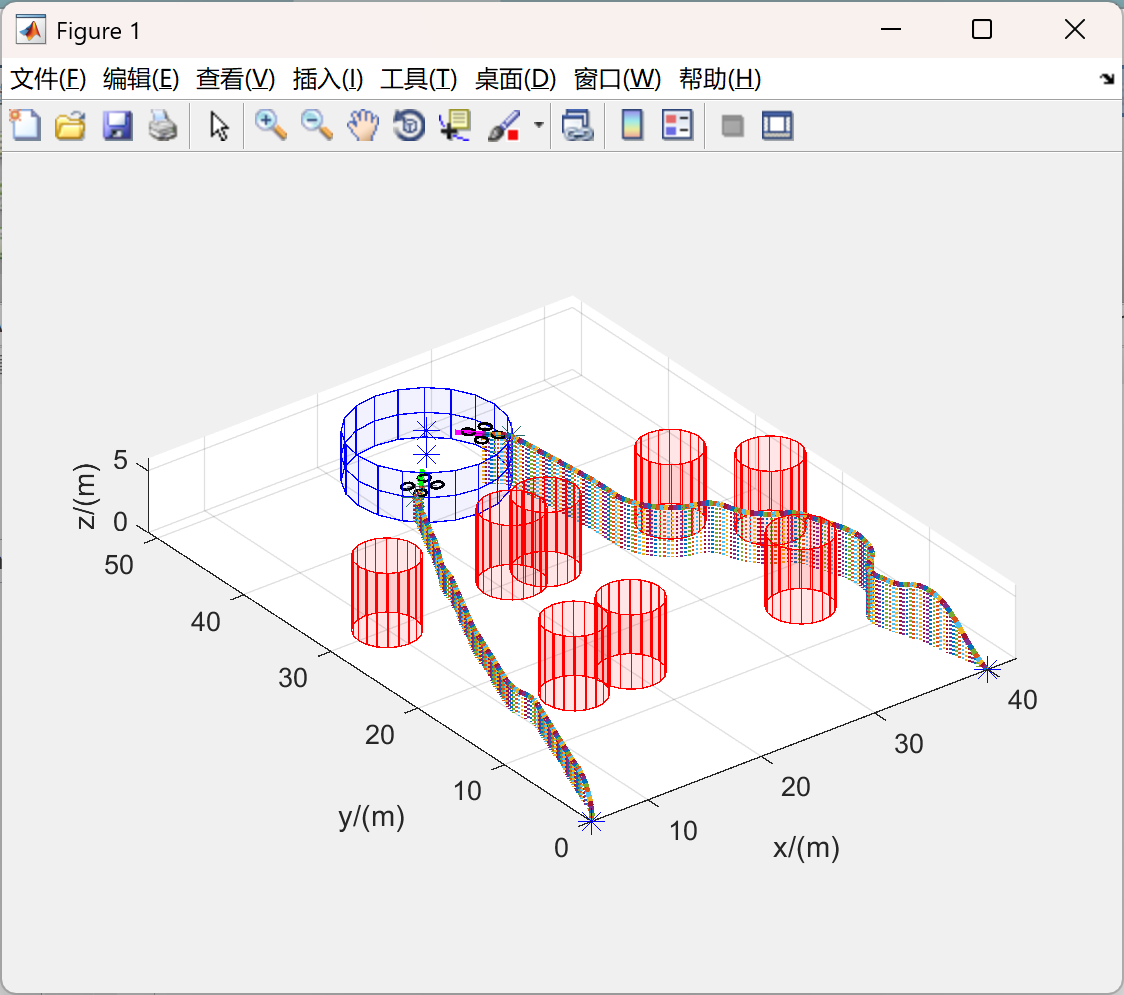
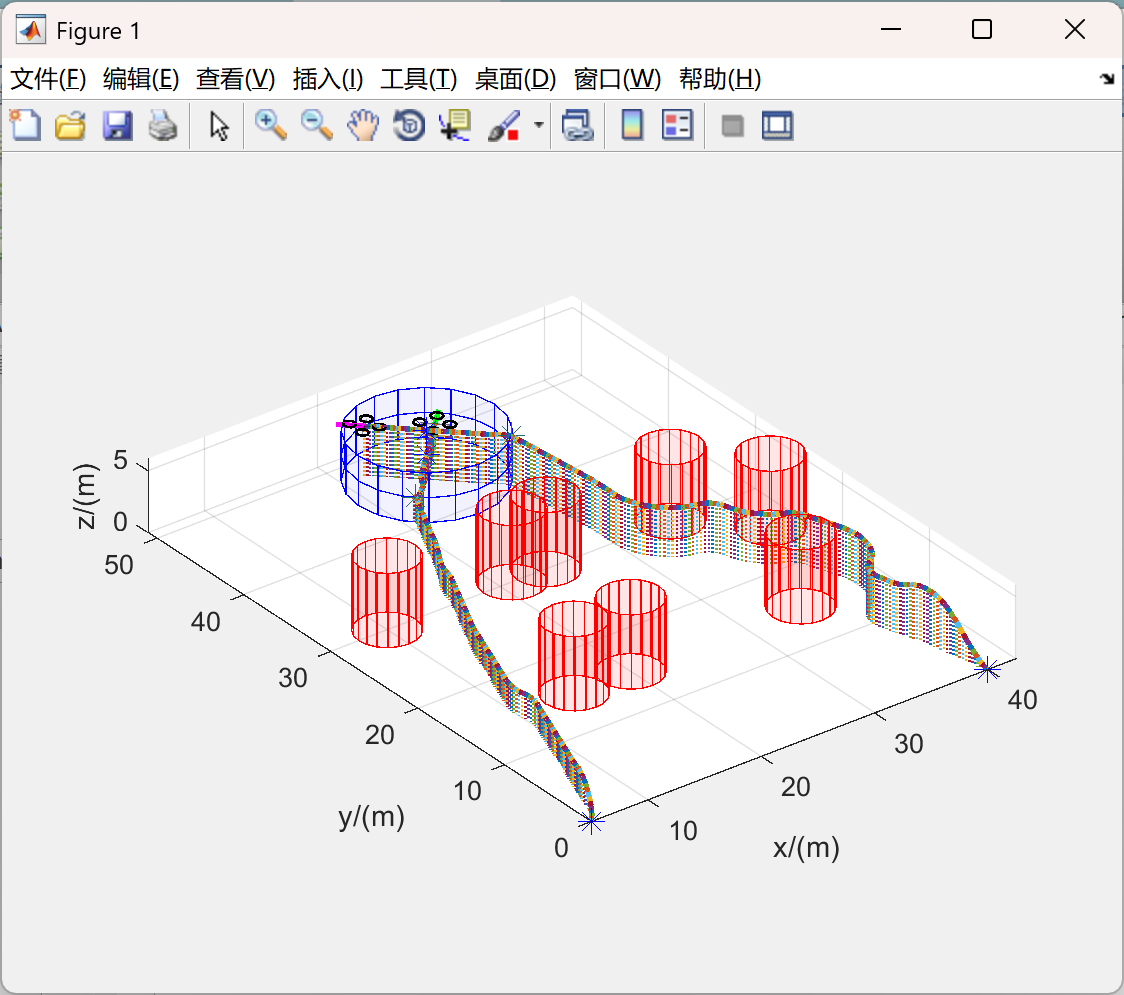
主函数部分代码:
clc
clear all
close all
%%
figure
axis([0 50 0 50 0 10]);
axis equal
xlabel('x/(m)')
ylabel('y/(m)')
zlabel('z/(m)')
view(3)
grid on
%上色选择
rng(1)
all_colors = rand(6,3);
%%
%。。。。。。。数据记录。。。。。。
bag=zeros(6,300);
%%
%。。。。。。。数据记录。。。。。。
bag2=zeros(6,300);
%%
%。。。。。。。初始点-终止点。。。。。。。。
begin=[5,0];
over=[25,45];
%%
%。。。。。。。初始点-终止点。。。。。。。。
begin2=[40,0];
% over=[25,45];
%%
%。。。。。。。虚拟导引点。。。。。
r_gui=6; %虚拟导引半径guide
theta_gui=-0.75*pi; %虚拟导引点的夹角
v_target=0; %目标运动速度
over_gui=over+r_gui*[cos(theta_gui),sin(theta_gui)]; %给虚拟导引点赋值
%%
%。。。。。。。虚拟导引点。。。。。
% r_gui=5; %虚拟导引半径guide
theta_gui2=-0.25*pi; %虚拟导引点的夹角
% v_target=0; %目标运动速度
over_gui2=over+r_gui*[cos(theta_gui2),sin(theta_gui2)]; %给虚拟导引点赋值
%%
%。。。。。。。障碍物位置。。。。。。。。
obstacle=[15 35 10 24 40 20 21 35; ...
15 15 30 30 25 15 30 30];
%%
%。。。。。。。是否可视化无人机。。。。。。。
vision_uav=1;
%%
%。。。。。。。是否可视化无人机。。。。。。。
vision_uav2=1;
%%
%。。。。。。。协同标志位。。。。。。。。
flag_co=0; %cooperate
%%
%。。。。。。。协同标志位。。。。。。。。
flag_co2=0; %cooperate
%%
accu=0;
accu2=0;
accu_time=0;
%%
%。。。。。。。初始化参数。。。。。。。。。。。
v=3; %每次迭代的速度m/s
delta_t=0.1; %时间间隔
t_end=200; %最大仿真时间
iters=1; %迭代次数初始化
%%
curr=[begin';0]; %当前位置
curr_previous=curr; %上一刻位置
%%
curr2=[begin2';0]; %当前位置
curr_previous2=curr2; %上一刻位置
%%
testR=v*delta_t; %测试圆的半径
Q_star=5; %障碍物涉及的半径
num_point=36; %周围的势能点个数
testPoint=zeros(num_point,2); %周围8个点的坐标数组(x,y)
testOut=zeros(1,num_point); %周围8个点的势能??
step_predict=10; %预测步长
%%
pos_predict=zeros(step_predict,3); %预测域内的位置数组(x,y,z),z信息固定
%%
pos_predict2=zeros(step_predict,3); %预测域内的位置数组(x,y,z),z信息固定
%%
%。。。。。。。预测点加上z轴信息。。。。。。。。
h=2;
pos_predict(:,3)=h; %无人机飞行定高为(m)
%%
%。。。。。。。预测点加上z轴信息。。。。。。。。
h2=4;
pos_predict2(:,3)=h2; %无人机飞行定高为(m)
%%
%。。。。。。。画无人机所需的参数。。。。。。。。。
roll_max=5;
pitch_max=5;
%%
U_k=zeros(3,1);
%%
U_k2=zeros(3,1);
%%
%。。。。。。。。画初始点。。。。。。。。
hold on;
plot3(begin(1),begin(2),0,'*b','MarkerSize',10);
%%
plot3(begin2(1),begin2(2),0,'*b','MarkerSize',10);
%%
%。。。。。。。画目标的圆形范围。。。。。。。。
plot_target(over(1),over(2),h,r_gui)
%%
%。。。。。。。画目标的圆形范围。。。。。。。。
plot_target(over(1),over(2),h2,r_gui)
%%
%。。。。。。。。。MPC初始参数。。。。。。。。。。。
A=[zeros(3),eye(3);
zeros(3),zeros(3)]*delta_t+ ...
eye(6); %状态矩阵A初始条件x_k,权重矩阵Q,R及终端误差矩阵F为输入
B=[0.5*eye(3)*delta_t^2;eye(3)*delta_t]; %输入矩阵B
N=step_predict; %预测长度
%%
x_k=[begin(1);begin(2);0;
0*ones(3,1)]; %当前状态,初始化
🎉3 参考文献
文章中一些内容引自网络,会注明出处或引用为参考文献,难免有未尽之处,如有不妥,请随时联系删除。
[1]孙绍芳,鲁亚飞,邵帅,等.战术侦察无人机装备应用发展综述[J/OL].航空工程进展,1-15[2025-07-20].http://kns.cnki.net/kcms/detail/61.1479.V.20250717.1455.002.html.
[2]陈守阔,陈景豪,田宇翔,等.集成智能AI的无人机巡检任务规划算法[J].东北电力技术,2025,46(07):18-22.
🌈4 Matlab代码实现





















 1723
1723

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








