UVA1425 - Metal

最新推荐文章于 2023-05-09 22:41:27 发布

原创最新推荐文章于 2023-05-09 22:41:27 发布 · 232 阅读

1 ·

CC 4.0 BY-SA版权

一般动态规划同时被 2 个专栏收录

113 篇文章

订阅专栏

计算几何

18 篇文章

订阅专栏

本文介绍了一种使用动态规划(DP)解决特定凸包问题的方法。通过定义状态fij表示上壳结束于点i，下壳结束于点j时的情况，文章详细阐述了如何进行状态转移，包括将新点加入上壳或下壳的条件判断，以及对应的代码实现。

链接

https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=4171

题解

我可以把这个图形分成上壳和下壳
$f_{ij}$ 表示上壳的结束点是编号为 $i$ 的点，下壳的结束点是编号为 $j$ 的点
那么显然 $1$ 到 $m a x (i, j)$ 这些点都已经包含在图形中了
假设不妨设 $i < j$ ，假设有如下情形
在这里插入图片描述
因为 $i < j$ 所以把第 $j + 1$ 个点加入到下面的线段上可定是可以的
即 $f_{i,j+1}+=f_{ij}$ ，如下

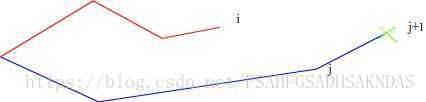
如果将第 $j + 1$ 个点加入到上壳中，且不会使得第 $i + 1$ 到第 $j$ 个点在线段新产生的线段的上方，就可以将第 $j + 1$ 个点加入到上壳中，如下图
即 $f_{j+1,j}+=f_{ij}$
在这里插入图片描述
反之则无法转移，如下图

代码

//dp、几何
#include <bits/stdc++.h>
#define maxn 55
#define eps 1e-8
#define cl(x) memset(x,0,sizeof(x))
#define ll long long
using namespace std;
struct point
{
	double x, y;
	point(double xx, double yy){x=xx, y=yy;}
	point(){}
}pt[maxn], _(0.0,0.0);
struct vec
{
	point pt;
	double x, y;
	vec(point p, double xx, double yy){pt=p, x=xx, y=yy;}
	vec(){}
};
ll f[maxn][maxn], N;
bool operator<(point p1, point p2){return p1.x<p2.x-eps;}
double operator*(vec v1, vec v2){return v1.x*v2.y-v2.x*v1.y;}
vec operator-(point p1, point p2){return vec(_,p2.x-p1.x,p2.y-p1.y);}
ll read(ll x=0)
{
	ll c, f=1;
	for(c=getchar();!isdigit(c);c=getchar())if(c=='-')f=-1;
	for(;isdigit(c);c=getchar())x=(x<<1)+(x<<3)+c-48;
	return f*x;
}
void init()
{
	ll i;
	N=read();
	for(i=1;i<=N;i++)pt[i].x=read(), pt[i].y=read();
	sort(pt+1,pt+N+1);
}
void dp()
{
	ll i, j, k, ans=0;
	cl(f);
	f[1][1]=1;
	for(i=1;i<=N;i++)
	{
		for(j=1;j<=i;j++)
		{
			if(i==j and i!=1)continue;
			f[i+1][j]+=f[i][j];
			f[j][i+1]+=f[j][i];
			if(i==j)continue;
			for(k=j+1;k<=i;k++)if((pt[i+1]-pt[j])*(pt[k]-pt[j])<eps)break;
			if(k>i)f[i][i+1]+=f[i][j];
			for(k=j+1;k<=i;k++)if((pt[i+1]-pt[j])*(pt[k]-pt[j])>-eps)break;
			if(k>i)f[i+1][i]+=f[j][i];
		}
	}
	printf("%lld\n",f[N-1][N]+f[N][N-1]);
}
int main()
{
	ll T=read();
	while(T--)
	{
		init();
		dp();
	}
	return 0;
}