方格填数

方格填数
如图，如下的10个格子，填入0~9的数字。要求：连续的两个数字不能相邻。 
（左右、上下、对角都算相邻）一共有多少种可能的填数方案？ 
请填写表示方案数目的整数。

解题思路：

从左到右，从上到下依次填写数字

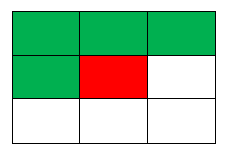
对于红色方格来说，只有绿色方格是已经填好数字了，因此，要在红色方格中填写正确的数字，只要满足两个条件即可。

1.所要填写的数字是否已经被其他格子占用；

2.与绿色格子中的数字之差是否为1；

源码附上：

#include <bits/stdc++.h>
using namespace std;
int A[3][4];
int nums[10];
int dir[4][2]={-1,-1,-1,0,-1,1,0,-1};
int cou=0;

int check(int x,int y,int k)
{
	for(int i=0;i<4;i++)
	{
		int xx=x+dir[i][0];
		int yy=y+dir[i][1];
		if(xx<0||xx>2||yy<0||yy>3)
			continue;
		if(abs(A[xx][yy]-k)==1)
			return false;
	}
	return true;
}

void dfs(int x,int y)
{
	if(x==2&&y==3)
	{
		cou++;
		return;
	}
	if(y>3)
	{
		y=0;
		x=x+1;
	}
	for(int i=0;i<=9;i++)
	{
		if(nums[i]==0&&check(x,y,i))
		{
			nums[i]=1;
			A[x][y]=i;
			dfs(x,y+1);
			nums[i]=0;
			A[x][y]=-10;
		}
	}
}

int main()
{
	memset(A,-10,sizeof(A));
	dfs(0,1);//从0，1出发 
	cout<<cou<<endl;
	return 0;
}

做dfs的惯性思维：总是向它的左上右下移动，其实并不然，要合理正确灵活的应用，根据实际需求出发。