【强化学习基础算法】基础算法:贪婪算法 策略迭代 价值迭代 Sarsa Q-learning核心思想简介

贪婪算法

适用于无状态问题(多臂老虎机)

$ϵ$-贪婪算法

• 大概率根据已有知识选择奖励最高的行为（利用），小概率随机选择行为，增加对环境的认识（探索）
  

递减的$ϵ$-贪婪算法

• 探索的概率随时间（对环境认知增多后）逐渐衰减
  

上置信界算法UCB

• 多探索那些很少被访问的机器
• 一种经典的基于不确定性的策略算法，引入不确定性度量$U(a)$,其会随着一个动作被尝试次数的增加而减小
• 引入不确定性度量U(a)，不确定性越高，就越具有探索的价值，因为探索之后可能发现它的期望奖励很大。随着一个动作被尝试次数的增加，不确定性度量减小。
• 使用一种基于不确定性的策略来综合考虑现有的期望奖励估值和不确定性，其核心问题是如何估计不确定性。
• UCB 算法在每次选择拉杆前，先估计每根拉杆的期望奖励的上界，使得拉动每根拉杆的期望奖励只有一个较小的概率p超过这个上界，（因为当p很小时，1-p很大，则$Q(a_t)$<$Q(\widehat{a_t})$+ $U(\widehat{a_t})$成立的概率很大）接着选出期望奖励上界最大的拉杆，从而选择最有可能获得最大期望奖励的拉杆。上标^代表估计量

汤普森采样法

• 使用beta分布衡量期望
• 汤普森采样，先假设拉动每根拉杆的奖励服从一个特定的概率分布（beta分布），然后根据拉动每根拉杆的期望奖励来进行选择。
  
• 由于计算所有拉杆的期望奖励的代价比较高，汤普森采样算法使用采样的方式，即根据当前每个动作$a$的奖励概率分布进行一轮采样，得到一组各根拉杆的奖励样本，再选择样本中奖励最大的动作。
• 汤普森采样是一种计算所有拉杆的最高奖励概率的蒙特卡洛采样方法。

基于动态规划的强化学习算法

• 策略迭代中的策略评估使用贝尔曼期望方程来得到一个策略的状态价值函数，这是一个动态规划的过程
• 价值迭代直接使用贝尔曼最优方程来进行动态规划，得到最终的最优状态价值
• 基于动态规划的这两种强化学习算法要求事先知道环境的状态转移函数和奖励函数，也就是需要知道整个马尔可夫决策过程
• 在这样一个白盒环境中，不需要通过智能体和环境的大量交互来学习，可以直接用动态规划求解状态价值函数。但是，现实中的白盒环境很少，这也是动态规划算法的局限之处，我们无法将其运用到很多实际场景中
• 策略迭代和价值迭代通常只适用于有限马尔可夫决策过程，即状态空间和动作空间是离散且有限的

策略迭代

• 由策略评估和策略提升两部分组成
• 策略评估：已知马尔科夫决策过程和策略，计算状态价值函数$V^{\pi }(s)$，评估每个状态的价值
• 策略提升：根据每个状态的价值（状态价值函数），计算动作价值函数$Q(s,a)$，重新计算每个动作的概率，即选择Q函数最大值的动作
• 在策略迭代里面，在初始化的时候，我们有一个初始化的状态价值函数 和 策略 ，然后在策略评估和策略提升这两个步骤之间进行迭代
  

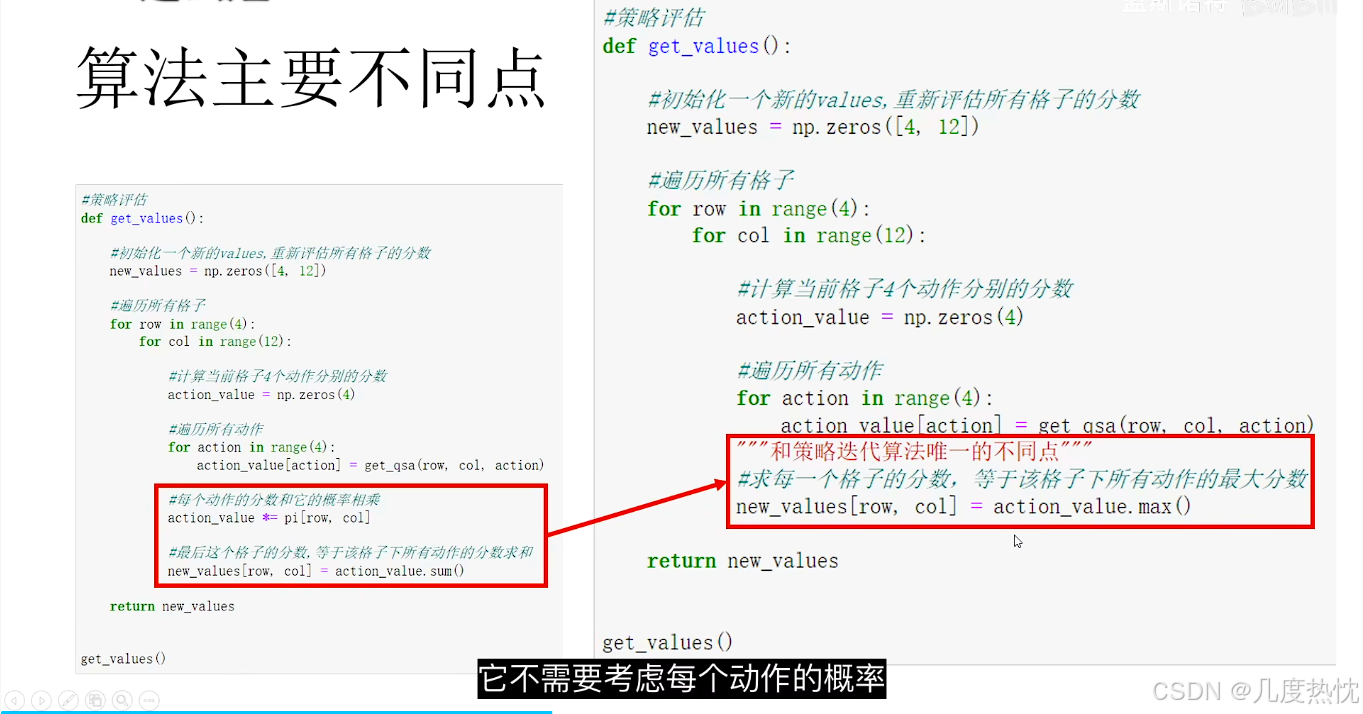
价值迭代

• 价值迭代算法不需要考虑每个动作的概率，在每个状态下的价值直接等于该状态下动作所能取得的最高分数
  

时序差分算法

Sarsa算法

• 无模型的在线学习算法
• 无模型是指 状态转移未知，奖励函数已知，没有上帝视角
• 在强化学习中，在线学习指智能体与环境实时交互，根据当前策略选择动作，并立即更新策略。与离线学习不同，在线学习不需要预先收集大量数据，而是边交互边学习
• 更新公式如下所示：
  $$\begin{array}{r}Q(S_t,A_t)\leftarrow Q(S_t,A_t)+\alpha [R_{t+1}+\gamma Q(S_{t+1},A_{t+1})-Q(S_t,A_t)]\end{array}$$
• 核心思想是计算更新量 公式思想为$Q(S_t,A_t)=Q(S_t,A_t)+\alpha \Delta$
• 更新公式的主要涉及 $S,A,R,S,A$， 因此称为sarsa算法

N步sarsa算法

• 核心思想：玩了N步之后更新第一步的对应价值函数
• 将$G_t=r_t+\gamma Q(s_{t+1},a_{t+1})$替换为$G_t=r_t+\gamma r_{t+1}+\dots +{\gamma }^{n}Q(s_{t+n},a_{t+n})$
  $$\begin{array}{rl}单步Sarsa：Q(s_t,a_t)& \leftarrow Q(s_t,a_t)+\alpha [r_t+\gamma Q(s_{t+1},a_{t+1})-Q(s_t,a_t)]\\ 多步Sarsa：Q(s_t,a_t)& \leftarrow Q(s_t,a_t)+\alpha [r_t+\gamma r_{t+1}+\dots +{\gamma }^{n}Q(s_{t+n},a_{t+n})-Q(s_t,a_t)]\end{array}$$

Q-learning

• 除了 Sarsa，还有一种非常著名的基于时序差分算法的强化学习算法——Q-learning

• Q-learning 和 Sarsa 的最大区别在于 Q-learning 的时序差分更新方式为
  $$\begin{array}{rl}Q(s_t,a_t)& \leftarrow Q(s_t,a_t)+\alpha [r_t+\gamma \underset{a}{\max }Q(s_{t+1},a)-Q(s_t,a_t)]\end{array}$$
  

• Q-learning 的更新并非必须使用当前贪心策略$arg{\max }_{a}Q(s,a)$采样得到的数据

• 给定任意$(s,a,r,s^{\prime })$都可以直接根据更新公式来更新$Q$

• 为了探索，通常使用一个$ϵ$-贪婪策略来与环境交互。Sarsa 必须使用当前$ϵ$–贪婪策略采样得到的数据，因为它的更新中用到的的是当前策略在$s^{\prime }$下的动作。称 Sarsa 是在线策略（on-policy）算法，称 Q-learning 是离线策略（off-policy）算法

• Q-learning在更新过程中总是选择当前状态下的最大动作价值对应的动作，而不考虑当前策略是如何选择动作的

DynaQ算法

• 有离线学习的成分，进行数据的反刍 温故而知新
• 上文提到的Sarsa和Q-learning，这些算法数据都是用一次之后就丢弃，走一步计算一步，对数据的利用率不高
• DynaQ在其基础上，增加离线学习，提高数据利用率
• 将历史经验存起来，更新时 随机从存起来的历史经验中随机挑选S,A,R,S,A计算更新量用于Q(s,a)的更新
• DynaQ在Q-learning的基础上进行了离线学习的改进

DQN算法

原始DQN

• 以神经网络代替Q表,输入state和action输出对应的分数
• DQN增加经验回放池，提高数据利用率
• 加粗样式
  
• 训练流程：
  
• 固定目标Q网络（Fixed Target Q-Network）： DQN引入了两个神经网络，一个是主要的Q网络用于产生当前状态下的Q值估计，另一个是目标Q网络用于生成目标Q值。
• 目标Q网络的参数是由主要Q网络的参数定期拷贝得来，但这些参数不会在训练中被更新，而是固定一段时间后再进行更新。这个机制的作用是减少训练中的价值估计偏差，有利于提高训练的稳定性和收敛速度。通过固定目标Q网络，可以减少因为目标Q值的变化而引起的训练不稳定性，从而更好地学习到最优的Q值函数。
• Q值函数的学习目标：DQN的目标是学习状态-动作对的价值函数Q(s, a)，即在给定状态s下采取动作a的价值。因此，DQN的网络结构被设计为接收状态作为输入，并输出每个动作的Q值，而不需要直接输入动作

DoubleDQN

• double DQN的改进点是防止target的过高估计
• TD target：$r+\gamma {\max }_{a^{\prime }\in A}Q(s^{\prime },a^{\prime })$，以其作为真实值$y$
• TD error: $r+\gamma {\max }_{a^{\prime }\in A}{Q}_{\omega }(s^{\prime },a^{\prime })-Q_{\omega }(s,a)$
• 在DQN中 计算target是取$maxQ(s^{\prime },a^{\prime })$，易使得对target的过高估计
• 由于 max 操作，DQN 会倾向于高估 Q 值。这是因为 Q 值估计本身存在噪声，而 max 操作会放大这些噪声，导致对某些动作的 Q 值估计过高
• Double DQN 通过解耦动作选择和动作评估来解决过估计问题。具体来说，它使用两个网络：
  主网络（Main Network）：用于选择动作。
  目标网络（Target Network）：用于评估动作的 Q 值。
• Double DQN 避免了直接使用同一个网络同时进行动作选择和动作评估，从而减少了最大化偏差和过估计问题
• 相当于把动作的选择和分数的计算分别交给两个网络来计算，原来的DQN是一个网络既进行动作的选择也进行分数的计算
  

Dueling DQN

• 核心思想：通过引入优势函数（Advantage Function）和状态值函数（State Value Function）的分离，显著提升了 Q 值估计的效率和性能
  

• DQN需要有足够的数据才能使得Q网络估计的准确，否则Q网络更新不完全

• Dueling DQN通过 V网络和A网络 相加来代替Q网络，更新时仅更新A和V，同时约束A的值，迫使模型多更新V来影响Q
  
  

策略梯度算法

• 核心思想：不计算Q函数，根据reward来调整不同动作的概率
• 一类直接优化策略的强化学习算法。与基于值函数的方法（如 Q-learning）不同，策略梯度算法直接对策略进行参数化，并通过梯度上升来优化策略参数，以最大化期望回报

reinforce算法

• REINFORCE 算法的核心思想是通过 蒙特卡罗方法 采样轨迹，利用轨迹的回报来估计策略梯度，并通过梯度上升更新策略参数

Actor-Critic算法

• Actor-Critic 算法 是一种结合了 策略梯度（Policy Gradient） 和 时序差分 也就是值函数估计（Value Function）方法的强化学习算法
• 定义策略梯度模型和时序差分模型，①以时序差分模型计算TD error、更新量，计算时序差分的loss，②根据策略梯度模型计算每个动作的概率，计算策略梯度loss的导数

PPO

• PPO（Proximal Policy Optimization） 是一种基于策略梯度的强化学习算法，由 OpenAI 在 2017 年提出。PPO 是 TRPO（Trust Region Policy Optimization） 的改进版本，旨在通过简单的实现和高效的性能解决策略梯度算法中的高方差和训练不稳定问题
• PPO 的核心思想是通过限制策略更新的幅度，避免策略更新过大导致性能崩溃。具体来说，PPO 使用了一种 剪切目标函数（Clipped Objective），确保新策略与旧策略之间的差异不会太大
• 优势函数（Advantage Function）：衡量某个动作相对于平均动作的优势
  

DDPG算法

• DDPG（Deep Deterministic Policy Gradient）算法是一种结合了深度学习和确定性策略梯度的强化学习算法，主要用于解决连续动作空间的控制问题
• 可以看作可用于连读动作空间的DQN算法，与DQN一样，也可离线学习
• DDPG算法中共有4个模型
  • 演员（Actor）：负责学习策略函数，输出确定性动作。
  • 评论家（Critic）：负责学习Q函数，评估动作的价值
  • 为了稳定训练，DDPG引入了目标网络，包括目标演员网络和目标评论家网络
  • Critic模型的输入是state与action的拼接
• 目标网络的参数通过软更新（soft update）方式逐步更新，而不是直接复制主网络的参数
  
  

SAC算法

• 最大化Q函数的同时最大化Q函数的熵

• SAC的核心思想是在优化策略时，不仅最大化累积奖励，还最大化策略的熵。熵衡量策略的随机性，高熵策略更具探索性，有助于避免局部最优解。
  

• 熵加权系数也是一个可学习的参数

• 主要特点：
  最大熵目标：SAC在目标函数中加入熵项，平衡奖励最大化和探索。
  随机策略：SAC使用随机策略，增强探索能力。
  双Q网络：采用两个Q网络，取较小值作为目标，减少过估计问题。
  目标网络：使用目标网络提高训练稳定性。
  

模仿学习

• 模仿专家的动作，让别人无法分辨
• 用于模仿学习的数据仅需要state和action，无需reward

CQL算法

• 离线强化学习算法，学习过程中完全不需要更新数据
• CQL（Conservative Q-Learning）是一种用于离线强化学习（Offline Reinforcement Learning, Offline RL）的算法，由Sergey Levine团队于2020年提出。离线强化学习的特点是智能体只能从固定的、预先收集的数据集中学习，而不能与环境进行交互。CQL的核心目标是解决离线RL中的分布偏移（distributional shift）和过估计（overestimation）问题，从而在离线数据上学习到鲁棒且有效的策略。
• CQL的核心思想是通过在Q函数的学习过程中引入保守性，使得学习到的Q函数在数据分布之外的区域不会过度乐观。
• 惩罚数据分布之外的Q值：在Q函数的学习目标中，增加一个正则化项，惩罚那些在数据分布之外的Q值。
• 提升数据分布内的Q值：同时，确保在数据分布内的Q值能够准确反映真实的回报。

MPC算法

• 行动之前先仔细推演
• 需要的训练量较少，因为每一步的动作都进行了谨慎的推演
• 对数据的利用率较高

MBPO算法

• 核心思想:认为推演的数据也有学习的价值
• MBPO（Model-Based Policy Optimization，基于模型的策略优化）是一种结合了模型基强化学习（Model-Based RL）和无模型强化学习（Model-Free RL）优势的算法。它由Janner等人于2019年提出，旨在通过利用学习到的环境模型来提高策略优化的样本效率，同时避免传统模型基方法中的模型误差累积问题。
• MBPO的核心思想是通过学习一个环境模型（动力学模型），并利用该模型生成额外的模拟数据来辅助策略优化

参考文献

• 强化学习 简明教程 代码实战
• 上述教程的代码地址