CodeForces 492E Vanya and Field（拓展欧几里得）

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Vanya decided to walk in the field of size n × n cells. The field contains m apple trees, the i-th apple tree is at the cell with coordinates (x_i, y_i). Vanya moves towards vector (dx, dy). That means that if Vanya is now at the cell (x, y), then in a second he will be at cell 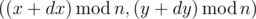. The following condition is satisfied for the vector: 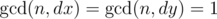, where 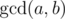is the largest integer that divides both a and b. Vanya ends his path when he reaches the square he has already visited.

Vanya wonders, from what square of the field he should start his path to see as many apple trees as possible.

Input

The first line contains integers n, m, dx, dy(1 ≤ n ≤ 10⁶, 1 ≤ m ≤ 10⁵, 1 ≤ dx, dy ≤ n) — the size of the field, the number of apple trees and the vector of Vanya's movement. Next m lines contain integers x_i, y_i (0 ≤ x_i, y_i ≤ n - 1) — the coordinates of apples. One cell may contain multiple apple trees.

Output

Print two space-separated numbers — the coordinates of the cell from which you should start your path. If there are several answers you are allowed to print any of them.

Examples

Input

5 5 2 3
0 0
1 2
1 3
2 4
3 1

Output

1 3

Input

2 3 1 1
0 0
0 1
1 1

Output

0 0

Note

In the first sample Vanya's path will look like: (1, 3) - (3, 1) - (0, 4) - (2, 2) - (4, 0) - (1, 3)

In the second sample: (0, 0) - (1, 1) - (0, 0)

题目大意：给定一个格子图，部分坐标位置 ( xi , yi ) 有苹果。给出一个偏移向量，每次只能按偏移量走，遇到走过的点就停下来。求一个出发点，使得经过的苹果最多。

推一推可以发现任意一个点出发按着偏移量走，能到的点是有限个，然后就开始重复。对于每个有苹果树的点必定有一个可以从（0，y）出发的点到它。对于每个（xi，yi）与它的出发点（x，y）有（x + ki * dx) % n = xi (1), (y + ki * dy) % n = yi (2) 。令 x = 0，又有 gcd（dx，n）= 1，可以用拓展欧几里得解出 k * dx + p * n = 1 。对于每个（xi，yi）可以计算出 ki = k * xi，进而计算出 y ，得到（0，y）即（xi，yi）的出发点 。统计一下每个（0，y）可以到的有苹果树的点，取最大即可。

#include<cstdio>
#include<algorithm>
#include<cstring>
#define ll long long
using namespace std;
const int maxn = 1e6 + 5;
int cou[maxn];
void exgcd(ll a,ll b,ll &x,ll &y)
{
    if(b == 0) x = 1,y = 0;
    else
    {
        exgcd(b,a % b,y,x);
        y -= x * (a / b);
    }
}
int main()
{
    memset(cou,0,sizeof(cou));
    ll n,m,dx,dy,x,y,ans,ma = 0;
    scanf("%I64d %I64d %I64d %I64d",&n,&m,&dx,&dy);
    ll k,temp;
    exgcd(dx,n,k,temp);
    for(int i = 0;i < m; ++i)
    {
        scanf("%I64d %I64d",&x,&y);
        if(x)
        {
            temp = k * x * dy % n;
            y = (y + n - temp) % n;
        }
        cou[y]++;
        if(cou[y] > ma)
        {
            ma = cou[y];
            ans = y;
        }
    }
    printf("0 %I64d\n",ans);
    return 0;
}