从维度出发：理解单头/多头注意力机制的计算

注意力机制：Self-Attention

注意力机制的计算公式非常简洁：
$$\text{Attention}(Q,K,V)=\text{softmax}(\frac{Q{K}^T}{\sqrt{d_k}})V,$$
其中$Q,K,V$之间的计算就是注意力机制的核心，也就是常说的：Query、Key和Value，从数学角度出发，这几个就是由向量所组成的矩阵，然后矩阵之间进行运算、缩放得到最终的输出结果，但纸上得来终觉浅，模型的知识还是需要实操才能得到更深入的理解，所以这里从注意力机制整个流程中计算维度的角度出发解释其计算流程，也更方便程序的编写。

现在假设输入的是一个特征矩阵$X$（或者可以理解为是一个句子，里面是词向量），其维度为
$$X:[N,input\_features],$$
$input\_features$即为每个特征向量的维度，再经过三个不加偏置的全连接层的计算，假设其对应矩阵为$W_Q,W_K,W_V$，其维度为
$$W_Q:[input\_features,head\_dim],$$
$$W_K:[input\_features,head\_dim],$$
$$W_V:[input\_features,head\_dim\_v],$$
$head\_dim$则理解为计算注意力权重过程中中间层的维度，然后将其与所输入的特征矩阵$X$进行矩阵乘法，得到前面所提到的$Q,K,V$矩阵：
$$Q:[N,head\_dim],$$
$$K:[N,head\_dim],$$
$$V:[N,head\_dim\_v].$$

得到所需的矩阵之后，代入注意力机制的计算公式进行计算，第一步就是$Q\times K^T$，由于这两个矩阵中的第一维就是表示需要分配注意力权重的维度：某个单词或者某个通道，所以这里矩阵$K$转置后的计算就是表示计算着两个矩阵中对应向量的内积，其维度变换为：
$$Q\times K^T:[N,head\_dim]\times [head\_dim,N]=[N,N],$$
后面的除以$\sqrt{d_k}$，也就是除以$head\_dim$，是为了重新将特征向量中的元素缩放到方差为1的分布中，并不会改变矩阵的维度；而$softmax$操作只是将每行映射为和为1的权重（后续用于分配不同的注意力权重给不同位置的$Value$向量），同样不会改变矩阵的维度，即：
$$\text{softmax}(\frac{Q{K}^T}{\sqrt{d_k}}):[N,N].$$

来到最后一步，按照上面的步骤可以轻易得出：
$$\begin{array}{rl}\text{softmax}(\frac{Q{K}^T}{\sqrt{d_k}})V& :[N,N]\times [N,head\_dim\_v]\\ & =[N,head\_dim\_v].\end{array}$$
到这里，整个注意力机制的计算过程就已经完成了，核心思想就是计算向量之间的内积并作为权重分配给不同特征向量，最终实现注意力机制的“注意力”功能。

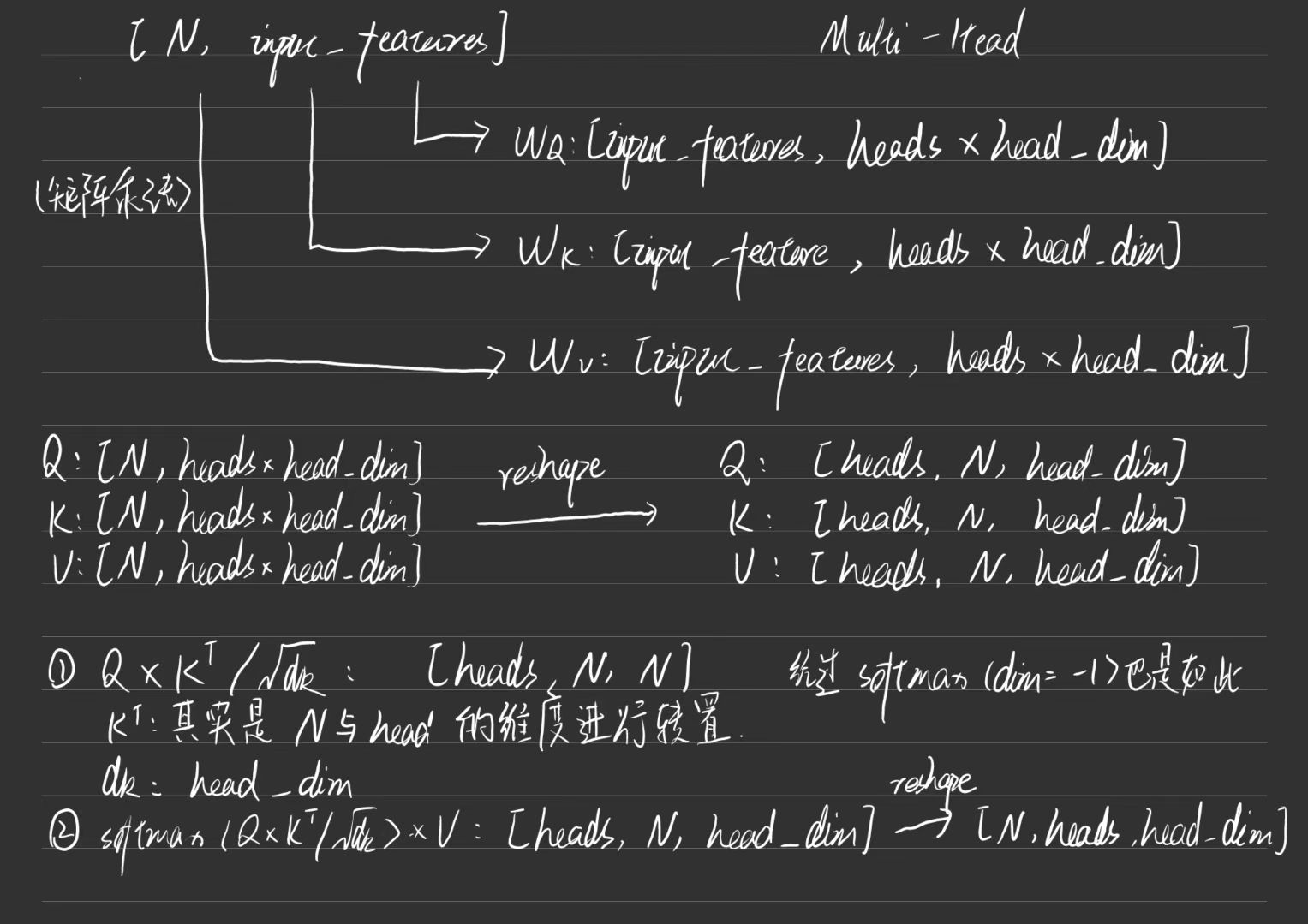
多头注意力机制：Multi-Head Attention

多头注意力机制就是对多个注意力机制的输出输出结果进行拼接：
$$\begin{array}{rl}\mathrm{MultiHead}(Q,K,V)& =\mathrm{Concat}({\mathrm{head}}_1,...,{\mathrm{head}}_{\mathrm{h}})W^O\\ \mathrm{where}\mathrm{hea}{\mathrm{d}}_{\mathrm{i}}& =\text{Attention}(Q{W}_i^Q,K{W}_i^K,V{W}_i^V)\end{array}$$
简单来说可以直接写多个Attention再使用拼接代码实现，但是也可以直接通过矩阵的拆分来实现，下面简单介绍下多头注意力机制中矩阵维度的变化。

同样的，假设输入的是一个特征矩阵$X$，其维度为
$$X:[N,input\_features],$$
$heads$即为多头注意力机制中的头数，同样经过三个不加偏置的全连接层，其对应矩阵为$W_Q,W_K,W_V$，其维度为
$$W_Q:[input\_features,heads\times head\_dim],$$
$$W_K:[input\_features,heads\times head\_dim],$$
$$W_V:[input\_features,heads\times head\_dim\_v],$$
其余符号含义和计算过程与上述类似，同样得到前面所提到的$Q,K,V$矩阵：
$$Q:[N,heads\times head\_dim],$$
$$K:[N,heads\times head\_dim],$$
$$V:[N,heads\times head\_dim\_v].$$

在进行进一步计算之前，需要对这些矩阵进行reshape一下：
$$Q:[heads,N,head\_dim],$$
$$K:[heads,N,head\_dim],$$
$$V:[heads,N,head\_dim\_v],$$
现在计算$Q\times K^T$，这里的对$K$进行转置其实就是对$N$和$head\_dim$的维度进行交换，这里包括后面的矩阵运算也都是在后面两个维度上进行的，可以得到：
$$\begin{array}{rl}Q\times K^T& :[heads,N,head\_dim]\times [heads,head\_dim,N]\\ & =[heads,N,N],\end{array}$$

同样的，经过缩放和$\text{softmax}$的计算后不会改变矩阵的维度，那么有：
$$\begin{array}{rl}\text{softmax}(\frac{Q{K}^T}{\sqrt{d_k}})V& :[heads,N,N]\times [heads,N,head\_dim\_v]\\ & =[heads,N,head\_dim\_v].\end{array}$$

主要的计算部分到这里已经结束了，需要进一步使用多头注意力机制的结果就可以在这个基础上进行reshape等操作。