*************
C++
leetcode:. - 力扣(LeetCode)
*************
首先看一眼题目:

这个形状一看,起手就是构造一个二维矩阵dp,初始化所有的元素为 0 。为什么呢,因为目前我只会矩阵。跟之前一样,我还是喜欢举个简单的例子,还是4 ✖️ 4的矩阵,方便理解,算了,还是举个5 ✖️ 5的,方便我理解。
| matrix | array | |||||||||||
| 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |||
| 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | |||
| 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | |||
| 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | |||
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |||
简单的理解就是,初始化一个 矩阵dp,然后熟练的将第一行 && 第一列填充,为什么使用 && 这个呢,是因为这个代表同时满足的意思, || 这个代表只要满足一个就行的意思。这个代码比较的简单。回头看这段代码的时候,是一眼就能发现一个问题的,应该是 int j;
| matrix | array | |||||||||
| 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | |
| 1 | 0 | 1 | 1 | 1 | 1 | |||||
| 1 | 1 | 1 | 1 | 1 | 1 | |||||
| 1 | 0 | 0 | 1 | 0 | 1 | |||||
| 1 | 0 | 0 | 0 | 0 | 1 | |||||
class Solution {
public:
int maximalSquare(vector<vector<char>>& matrix) {
int m = matrix.size; // get the rows
int n = matrix[0].size(); // get the columns
vector<vector<int>> dp(m, vector<int>(n, 0)); // initialise the array
// make dp the first row elements totally equal the first line of the matrix
for (j = 0; j < n; j++){
dp[0][j] = matrix[0][j];
}
}
};再然后就是填充剩下的一列,困难来到了怎么判断,这个时候来那个矩阵来帮助思考一下。最开始的想法就是填充以下的元素。最简单的想法就是 穷举法, 没错我很爱穷举法,主要是因为在妇联3,奇异博士穷举了好多种可能,最后取了一种。扯远了,话说回来,主要是因为穷举法最能顺应直觉,但是这里我不太会。
我还是喜欢矩阵多一点,矩阵向量,太妙了。因为只有数字0 or 1,所以第一行0就代表没有,1就代表有一个边长为1的正方形,因此直接复制第一行到dp。从dp[1][0]开始,也就是说第二行第一列开始,我们这里开始分析,右下角那个是最好分析的,为什么,因为左上角是固定的,右下角可以直接填充。
| matrix | array | |||||||||
| 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | |
| 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | |
| 1 | 1 | 1 | 1 | 1 | 1 | |||||
| 1 | 0 | 0 | 1 | 0 | 1 | |||||
| 1 | 0 | 0 | 0 | 0 | 1 | |||||
举例, dp[1][1]就是代表第二行第二列,如果是0的话,直接排除了当前单元格跟其他单元格组成正方形的可能性,因此对于是0的单元格,不能用1填充,在这里,不能让0和1相遇,会出问题的。dp[1][2]的值也是1,他不能与 左边 || 左上 || 正上方的格子组成一个正方形,所以只能是他自己组成一个正方形,所以边长是1。dp[1][3]同理,由于正上方是0,所以也不能组成边长是2的正方形。
| matrix | array | |||||||||
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 1 | 1 | 1 | 1 | 1 | 1 | 2 | 2 | 2 | 2 | |
| 1 | 1 | 1 | 1 | 1 | 1 | 2 | 3 | 3 | 3 | |
| 1 | 1 | 1 | 1 | 1 | 1 | 2 | 3 | 4 | 4 | |
| 1 | 1 | 1 | 1 | 1 | 1 | 2 | 3 | 4 | 5 | |
这里并不能总结出什么规律,但是稍微查一下就知道这里有一个很多简单的方法可以借鉴,就是 dp[i][j]的数值是由dp[i][j - 1] && dp[i - 1][j] && dp[i - 1][j - 1]共同决定的,即dp[i][j] = min(dp[i][j - 1] , dp[i - 1][j] , dp[i - 1][j - 1]) + 1。具体的原理是什么呢,举例: 如上图,很好理解,我解释不出来,但是很好记,就是在最小值上+1就行。因此填充下面的代码就变得简单起来。
class Solution {
public:
int maximalSquare(vector<vector<char>>& matrix) {
int m = array.size(); // get the rows
int n = array[0].size(); // get the columns
vector<vector<int>> dp(m, vector<int>(n, 0)); // initialise the array and make the elements equal 0
// initialise the first row
for (int j = 0; j < n; j++){
dp[0][j] = matrix[0][j];
}
// initialise the first column
for (int i = 0; i < m; i++){
dp[i][0] = matrix[i][0];
}
// fill the rest of the elements
for (int i = 1; i < m; i++){
for (int j = 1; j < n; j++){
if (matrix[i][j] == 0){
dp[i][j] = 0;
} else {
dp[i][j] = min(dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]) + 1;
}
}
}
}
};这里的主要的代码就写好了,但是这题目的要求是算面积,这一步只找到了最大的正方形的边长。上过小学的都知道这里的门道有多深,正方形的面积等于边长的平方,因此可以补充剩下的return 代码。
class Solution {
public:
int maximalSquare(vector<vector<char>>& matrix) {
int m = array.size(); // get the rows
int n = array[0].size(); // get the columns
vector<vector<int>> dp(m, vector<int>(n, 0)); // initialise the array and make the elements equal 0
// initialise the first row
for (int j = 0; j < n; j++){
dp[0][j] = matrix[0][j];
}
// initialise the first column
for (int i = 0; i < m; i++){
dp[i][0] = matrix[i][0];
}
// fill the rest of the elements
for (int i = 1; i < m; i++){
for (int j = 1; j < n; j++){
if (matrix[i][j] == 0){
dp[i][j] = 0;
} else {
dp[i][j] = min(dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]) + 1;
}
}
int macSide = max(dp[i][j]);
}
int maximalSquare = maxSide * maxSide;
return maximalSquare;
}
};这里运行一下,不出意外的报错了。
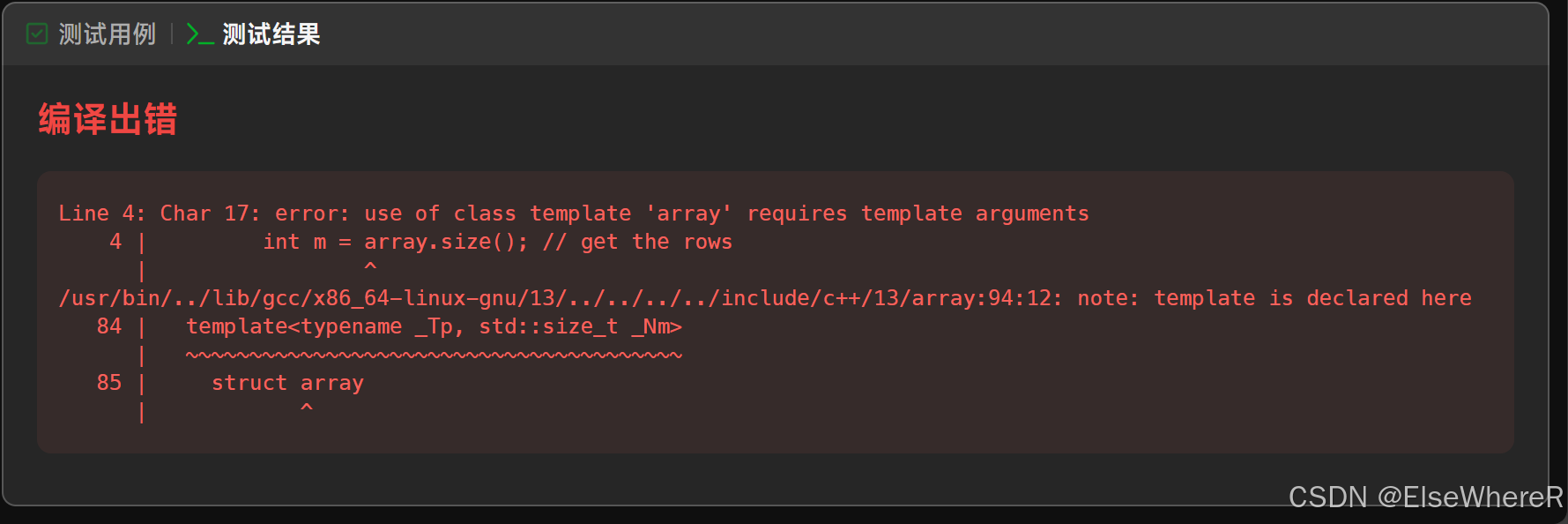
简单的分析一下,最开始给的是matrix而不是array,所以换掉。
其次是min的语法错了,这里改一下语法。
当然最重要的是,matrix是char类型,dp是 int 类型,需要转化。
最终改正完全的代码是这样的
class Solution {
public:
int maximalSquare(vector<vector<char>>& matrix) {
int m = matrix.size(); // get the rows
int n = matrix[0].size(); // get the columns
vector<vector<int>> dp(m, vector<int>(n, 0)); // initialise the array and make the elements equal 0
// initialise the first row
for (int j = 0; j < n; j++){
dp[0][j] = int(matrix[0][j]) - '0'; // convert char into int
}
// initialise the first column
for (int i = 0; i < m; i++){
dp[i][0] = int(matrix[i][0]) - '0'; // convert char into int
}
// fill the rest of the elements
int maxSide = 0; // creat a place to store the longest side
for (int i = 1; i < m; i++){
for (int j = 1; j < n; j++){
if (matrix[i][j] == '0'){
dp[i][j] = 0;
} else {
dp[i][j] = min({dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]}) + 1;
}
maxSide = max(maxSide, dp[i][j]);
}
}
int maximalSquare = maxSide * maxSide;
return maximalSquare;
}
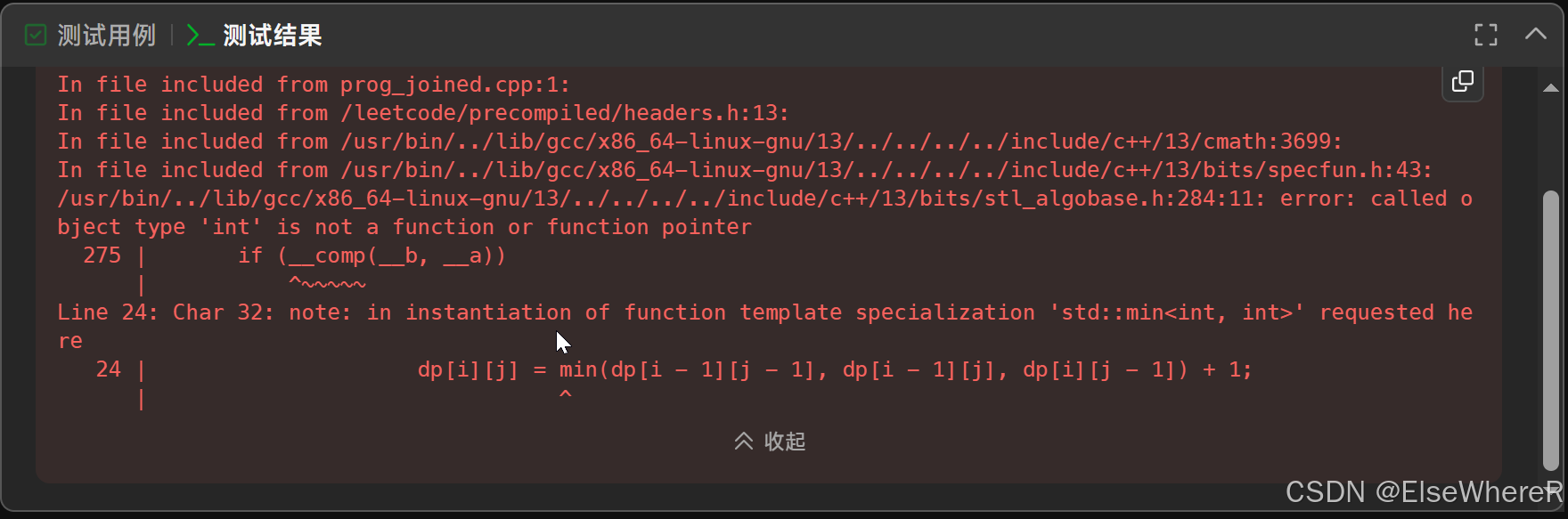
};这段代码是能跑起来的,但是还是错误了,为什么的呢?
这里需要重新检查一下代码,最大的边长需要在一开始就得初始化,一个解决方法是这样的,随时更新maxSide.
class Solution {
public:
int maximalSquare(vector<vector<char>>& matrix) {
int m = matrix.size(); // get the rows
int n = matrix[0].size(); // get the columns
vector<vector<int>> dp(m, vector<int>(n, 0)); // initialise the array and make the elements equal 0
int maxSide = 0; // creat a place to store the longest side
// initialise the first row
for (int j = 0; j < n; j++){
dp[0][j] = matrix[0][j] - '0'; // convert char into int
maxSide = (maxSide, dp[0][j]);
}
// initialise the first column
for (int i = 0; i < m; i++){
dp[i][0] = matrix[i][0] - '0'; // convert char into int
maxSide = max(maxSide, dp[i][0]);
}
// fill the rest of the elements
for (int i = 1; i < m; i++){
for (int j = 1; j < n; j++){
if (matrix[i][j] == '0'){
dp[i][j] = 0;
} else {
dp[i][j] = min({dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]}) + 1;
}
maxSide = max(maxSide, dp[i][j]);
}
}
int maximalSquare = maxSide * maxSide;
return maximalSquare;
}
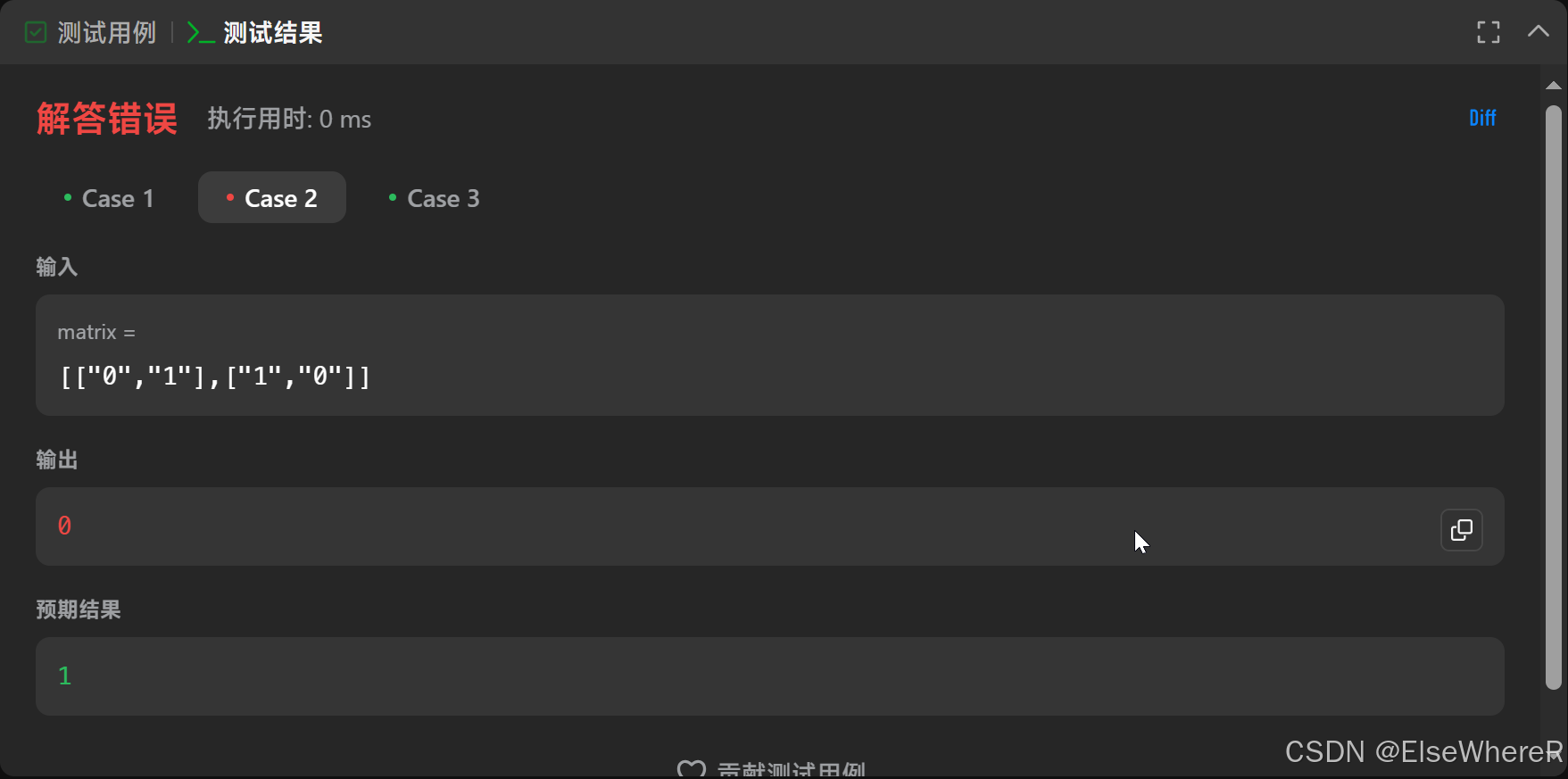
};如果我不想随时更新maxSide怎么办呢?那就看一下代码到底哪里出错了。以Case 2 为例:
| matrix | dp | |||
| 0 | 1 | 0 | 0 | |
| 1 | 0 | 0 | 0 | |
第一步肯定是将dp初始化为0;
| matrix | dp | |||
| 0 | 1 | 0 | 1 | |
| 1 | 0 | 1 | 0 | |
第二步是将第一行 && 第一列填充
| matrix | dp | |||
| 0 | 1 | 0 | 0 | |
| 1 | 0 | 0 | 0 | |
第三步是将第二行 && 第二列填充 ,这里的代码是
如果该单元格为0,那么dp填充0;否则才计数。
感觉是这里出了问题,换一下先后顺序。改成:
如果单元格是1,进行计数;如果单元格不是1,就填0;
这里的是没问题的,最后试了很多次,还是得更新第一行和第二行的maxSide的值。如果不更新的话,那么在第一行和第一列的时候就是维持初始值0。在填充第二行第二列的时候,maxSide的值依然维持是0。第27行开始,第二行第二列,应该是1 的,但是仅仅是因为没有更新,这里的原理我还不是很清楚。
dp[i][j] = min({dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]}) + 1;
// dp[1][1] = min(0, 1, 1) + 1没有关系,过几天再次看这个题目的时候,应该能理解。
最后,最终提交的代码是这个样子的:
class Solution {
public:
int maximalSquare(vector<vector<char>>& matrix) {
int m = matrix.size(); // get the rows
int n = matrix[0].size(); // get the columns
int maxSide = 0; // creat a place to store the longest side
vector<vector<int>> dp(m, vector<int>(n, 0)); // initialise the array and make the elements equal 0
// initialise the first row
for (int j = 0; j < n; j++){
dp[0][j] = matrix[0][j] - '0'; // convert char into int
if (dp[0][j] == 1) {
maxSide = 1; // update maxSide if there's a '1' in the first row
}
}
// initialise the first column
for (int i = 0; i < m; i++){
dp[i][0] = matrix[i][0] - '0'; // convert char into int
if (dp[i][0] == 1) {
maxSide = 1; // update maxSide if there's a '1' in the first column
}
}
// fill the rest of the elements
for (int i = 1; i < m; i++){
for (int j = 1; j < n; j++){
if (matrix[i][j] == '1'){
dp[i][j] = min({dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]}) + 1;
maxSide = max(maxSide, dp[i][j]);
}
// else {
// dp[i][j] = 0;
// }
}
}
int maximalSquare = maxSide * maxSide;
return maximalSquare;
}
};





















 683
683

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








