Day10: Gradient Descent

学习地址：李宏毅机器学习
参考博客：herosunly
在给定的函数空间中求解最佳函数，本质上是一个最优化问题，即求损失函数最小值对应的参数，然后将参数对应得到最佳函数。一种方法式解析解，但在机器学习中更加常用的是利用梯度下降求最小值。
若想深入学习梯度下降，可学习paper：An overview of gradient decent optimization algorithms，地址[1] [2]
1.梯度下降回顾

${\theta }_j^i$的上标表示第i组参数，下标表示该组参数的第j个值

2. 梯度下降的Tips
2.1调整学习率
下图是参数和损失值的曲线。若learning rate选取得很小（蓝色），loss需要很长时间才能达到；选取large learning rate（绿色）和非常大的学习率（黄色）会出现图中的情况。

因此，必须选区合适的学习率实现红色曲线的效果。
2.1.1时间衰减的学习率
时间衰减的学习率指的是随着时间增加，学习率逐渐减小。

2.1.2 Adagrad
核心思想：时间衰减后除以之前偏导平方和的平方根。


公式化简后的Adagrad:

简化后，分子与分母作用看起来相反：

直观解释

更为正式的解释：

最好的情况是：踏出的步伐和微分大小成正比。但需要讨论多个函数时，

通过二阶导数和一阶导数可以更快地接近最低点

2.2 随机梯度下降
根据计算梯度的样本个数，可分为批量梯度下降（全部样本）、小批量梯度下降（batch个数的样本）、随机梯度下降（单个样本）。


2.3特征缩放
特征缩放分为两种方法：归一化和标准化
举例：input两个特征
若$x_2$远大于$x_1$，使两者分布近似

归一化前后的对比结果，若未进行归一化，则

下图为标准化的表达式：
Feature Scaling

3.梯度下降理论
3.1可适用的范围
下列命题并不是恒成立的，比如遇到鞍点或者极值点（但不是最小值点）

3.2 数学简要证明
梯度下降的方法如下图所示：每次在一个小的邻域内得到最小值，然后行进到最小值点。

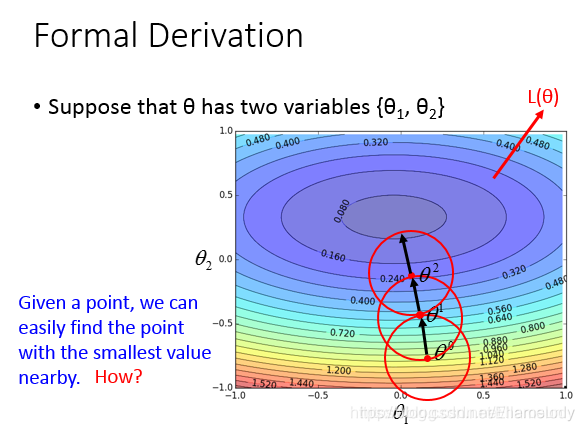
3.2.1 泰勒公式

阶次越高，则和$f(x)$越接近。

多元变量的泰勒公式表示和近似表示



将公式进行变换后：

得到最终的梯度下降公式：

• 作业
  归一化就是把不同维度的数据，通过缩放，设置为0到1之间
  feature scaling的计算顺序：先计算平均数和方差，结果是数值减去平均数后，再除以方差$$x_i^r\leftarrow \frac{x_i^r-m_i}{{\delta }_i}$$