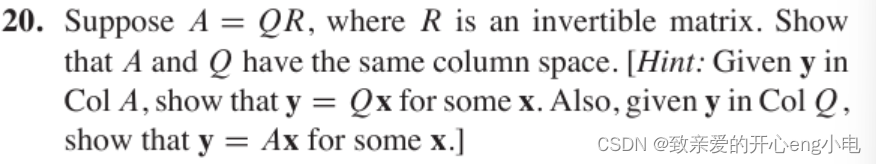【线性代数】6.4 exercise20

answer

To show that \( A \) and \( Q \) have the same column space, we'll use the given hints:

### Step 1: Show that \( \text{Col } A \subseteq \text{Col } Q \)
Given \( y \in \text{Col } A \), we can write \( y = Ax \) for some vector \( x \).

Since \( A = QR \) and \( R \) is invertible, we have:
\[ y = Ax = QRx \]

Let \( x' = Rx \). Since \( R \) is invertible, \( x' \) can be any vector in \(\mathbb{R}^n\). Thus:
\[ y = Qx' \]

This shows that \( y \) is also in the column space of \( Q \), i.e., \( \text{Col } A \subseteq \text{Col } Q \).

### Step 2: Show that \( \text{Col } Q \subseteq \text{Col } A \)
Given \( y \in \text{Col } Q \), we can write \( y = Qx \) for some vector \( x \).

Since \( A = QR \) and \( R \) is invertible,