Description
 Background
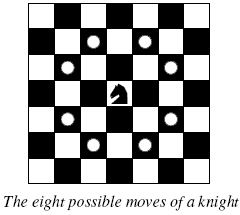
Background The knight is getting bored of seeing the same black and white squares again and again and has decided to make a journey
around the world. Whenever a knight moves, it is two squares in one direction and one square perpendicular to this. The world of a knight is the chessboard he is living on. Our knight lives on a chessboard that has a smaller area than a regular 8 * 8 board, but it is still rectangular. Can you help this adventurous knight to make travel plans?
Problem
Find a path such that the knight visits every square once. The knight can start and end on any square of the board.
Input
The input begins with a positive integer n in the first line. The following lines contain n test cases. Each test case consists of a single line with two positive integers p and q, such that 1 <= p * q <= 26. This represents a p * q chessboard, where p describes
how many different square numbers 1, . . . , p exist, q describes how many different square letters exist. These are the first q letters of the Latin alphabet: A, . . .
Output
The output for every scenario begins with a line containing "Scenario #i:", where i is the number of the scenario starting at 1. Then print a single line containing the lexicographically first path that visits all squares of the chessboard with knight moves
followed by an empty line. The path should be given on a single line by concatenating the names of the visited squares. Each square name consists of a capital letter followed by a number.
If no such path exist, you should output impossible on a single line.
If no such path exist, you should output impossible on a single line.
Sample Input
3 1 1 2 3 4 3
Sample Output
Scenario #1: A1 Scenario #2: impossible Scenario #3:A1B3C1A2B4C2A3B1C3A4B2C4
题目大意:给你p*q的棋盘,问你马能否以其中一格为起点遍历整个棋盘?如果可以,按字典序输出路径
思路表:打表字典序,若存在路径,则从A1开始即可遍历整个棋盘
AC代码如下:
<pre name="code" class="cpp">#include <iostream> #include <cstdio> #include <cstring> using namespace std; int p,q,flag1; int coun,cnt; int a[30][30]; char s[1000]; int dy[8] = {-2, -2, -1, -1, 1, 1, 2, 2}; int dx[8] = {-1, 1, -2, 2, -2, 2, -1, 1}; void dfs(int row,int col,int coun,int cnt) { if(row<1 || row>p || col<1 || col>q) return; if(cnt==p*q*2 && coun==p*q) { for(int i=0; i<cnt; i++) { printf("%c",s[i]); } cout<<endl<<endl; flag1=1; return; } a[row][col]=coun; for(int i=0; i<8 && flag1==0; i++) { if(row+dx[i]>=1 && row+dx[i]<=p && col+dy[i]>=1 && col+dy[i]<=q && a[row+dx[i]][col+dy[i]]==0) { a[row+dx[i]][col+dy[i]]=1; s[cnt]='A'+col+dy[i]-1; s[cnt+1]='1'+row+dx[i]-1; dfs(row+dx[i],col+dy[i],coun+1,cnt+2); a[row+dx[i]][col+dy[i]]=0; } } } int main() { int Case; cin>>Case; for(int flag=1; flag<=Case; flag++) { flag1=cnt=coun=0; memset(a,0,sizeof(a)); cin>>p>>q; printf("Scenario #%d:\n",flag); s[cnt]='A'; s[cnt+1]='1'; dfs(1,1,coun+1,cnt+2); if(flag1==0) cout<<"impossible"<<endl<<endl; } return 0; }
 骑士周游问题
骑士周游问题





















 965
965

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








