数字图像处理第三章——频域处理（上）

数字图像处理—频域处理

（一）二维离散傅里叶变换

基本定义：

1. 二维离散傅里叶变换：(Two-Dimensional Discrete Fourier Transform)是一种数字变换方法，一般应用于将图像从空间域转至频域，在图像增强、图像去噪、图像边缘检测、图像特征提取、图像压缩等等应用中都起着极其重要的作用。
2. 频谱：对一个时域信号进行傅里叶变换，就可以得到的信号的频谱，信号的频谱由两部分构成：幅度谱和相位谱，相位谱描述各个分量的相位随角频率的变化。幅度谱描述各个分量的幅度随着频率的变化。
3. 功率谱：为信号频谱的平方。可观察图像的能量分布，如果频谱图中暗的点数更多，那么实际图像是比较柔和的（因为各点与邻域差异都不大，梯度相对较小），反之，如果频谱图中亮的点数多，那么实际图像一定是尖锐的，边界分明且边界两边像素差异较大的。
4. 相位：表示相对于原始波形，这个波形的偏移量（左或右）。
5. 频域：频域就是频率域，平常我们用的是时域，是和时间有关的，这里只和频率有关，是时间域的倒数。时域中，X轴是时间，频域中是频率。频域分析就是分析它的频率特性。

进一步直观的理解这几个定义，编写代码如下：

h = imread('D:\数字图像处理\第三章学习\cat2.jpg');
f = im2double(rgb2gray(h));    %把图像变为灰度图像
F = fft2(f);                   %对图像进行傅里叶变换
FF = fftshift(F);              %对图像频谱进行移动，使0频率点在中心
s=log(abs(FF));                %获得傅里叶变换的幅度谱
p=log(angle(FF)*180/pi);       %获得傅里叶变换的相位谱
figure;
subplot(1, 3, 1), imshow(h), title('原图像');
subplot(1, 3, 2), imshow(s), title('图像的傅里叶变换幅度谱');
subplot(1, 3, 3), imshow(p), title('图像的傅里叶变换相位谱');

代码运行效果如下：

傅立叶频谱图上我们看到的明暗不一的亮点，实际是图像上某一点与邻域点差异的强弱，即梯度的大小，也即该点的频率的大小，图像中的低频部分（能量大，呈现白色）指低梯度的点，高频部分（能量小，呈现黑灰色）反之。

理论推导：

令f(x,y)代表一幅大小为 MxN的 数字图像，其中x=0,1,2,…,M-1, y=0,1,2,…,N-1, 由 F(u,v)表 示 的f(x,y)的二维离散傅立变换(DFT)可以由下式给出:

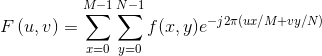
其中u=0,1,2,…,M-1,v=0,1,2,…,N-1。我们可以借助决定频率的变量 u、v(x和 y求和) 将指数形式展开为正弦和余弦的形式。频域系统是以 u,v(频率)为变量来表示 F(u, v)的坐标系。 离散傅立叶反变换(IDFT)的形式为：

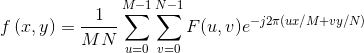
其中x=0,1,2,…,M-1,y=0,1,2,…,N-1。。因此，给定 F(u， v), 我们可以借助 IDFT(傅立叶反变换)来得到f(x,y)。

注意：由于 MATLAB中的 数组索引以1 开头，而不是以0 开头，MATLAB中的F(1,1)和f(1,1)对应数学公式中正变换和反变换的F(0,0)和f(0,0)。 一般而言，F(i,j)= F(i-1,j-1),且f(i,j)= f(i-1,j-1) i=1 2,…,M且j=1,2,…,N。

傅立叶谱可以定义如下：

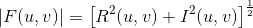
变换的相角定义如下:

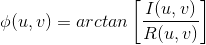
这两个函数可在极坐标形式下用于表示复函数F(u,v)：

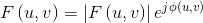
功率谱可以定义为幅度的平方:

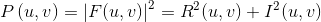
如果f(x,y)是实函数，它的傅立叶变换就是关于原点共轭对称的:

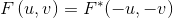
这意味着傅立叶谱也是关于原点对称的:

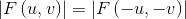
可以将它直接代入到公式 F(u,v)中:

F(u,v)= F(u+k1,M,v)=F(u,v+$k_2$