记录常见数学公式

最新推荐文章于 2025-09-08 19:36:37 发布

原创最新推荐文章于 2025-09-08 19:36:37 发布 · 728 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#高等数学

笔记专栏收录该内容

31 篇文章

订阅专栏

这篇博客探讨了基本不等式、导数和积分在信息技术中的重要作用。从曲率半径的计算到求导公式，再到特定积分的解法，展示了数学在解决信息技术问题中的核心地位。导数在优化算法、曲线拟合和数据分析中不可或缺，而积分则在处理连续变化和累积效果时发挥关键作用。理解这些数学概念对于深入理解和应用信息技术至关重要。

基本不等式

$11+x<ln(1+1x)<1x,(x>0)|a\pm b| \leq |a|+|b| \\ \space \\||a| - |b|| \leq |a - b| \\ \space \\ |\int_a^bf(x)dx| \leq \int_a^b|f(x)|dx \\ \space \\ \sqrt{ab} \leq \frac{a+b}{2} \leq \sqrt{\frac{a^2+b^2}{2}},(a, b>0) \\ \space \\ \sqrt[3]{abc} \leq \frac{a+b+c}{3} \leq \sqrt{\frac{a^2+b^2+c^2}{3}},(a, b,c>0) \\ \space \\ \frac{1}{1+x} <ln(1+\frac{1}{x})<\frac{1}{x}, (x>0)$

和差化积

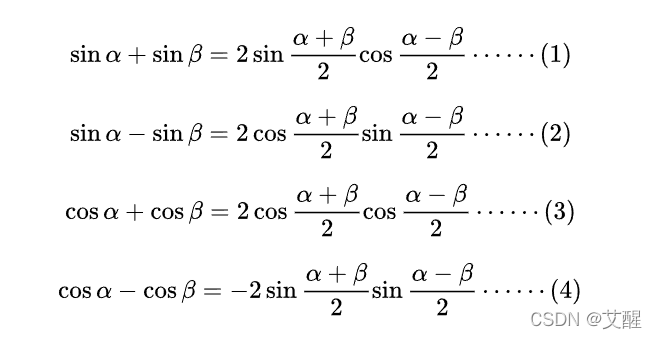
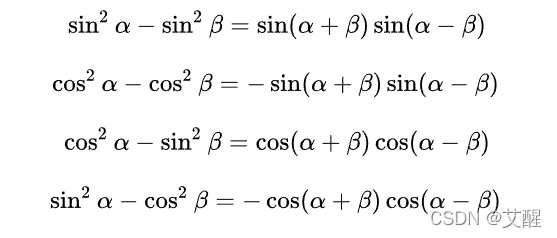
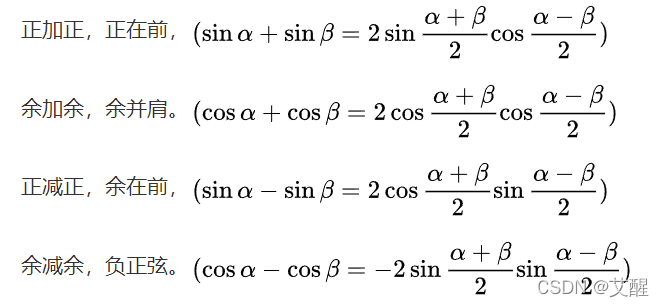
在这里插入图片描述

曲率半径

$R=∣(1+y′)32y′′∣R=|\frac{(1+y')^{\frac{3}{2}}}{y''}|$

求导公式（uv）’=uv’+u’v

$(uv)′=lim⁡Δx→0u(x+Δx)v(x+Δx)−u(x)v(x)Δx=lim⁡Δx→0u(x+Δx)v(x+Δx)−u(x)v(x)−u(x+Δx)v(x)+u(x+Δx)v(x)Δx=lim⁡Δx→0u(x+Δx)[v(x+Δx)−v(x)]+v(x)[u(x+Δx)−u(x)]Δx=uv′+u′v(uv)'=\lim_{\Delta x \to 0}\frac{u(x+\Delta x)v(x+\Delta x)-u(x)v(x)}{\Delta x} \\=\lim_{\Delta x \to 0} \frac{u(x+\Delta x)v(x+\Delta x)-u(x)v(x) - u(x + \Delta x)v(x)+ u(x + \Delta x)v(x)}{\Delta x} \\=\lim_{\Delta x \to 0} \frac{u(x+\Delta x)[v(x+\Delta x)-v(x)]+v(x)[u(x+\Delta x)-u(x)]}{\Delta x} \\=uv'+u'v$

导数公式

$\begin{aligned} &\int \frac{1}{cosx}dx =ln(|secx+tanx|)+C \\ &\int \frac{1}{sinx}dx =ln(|cscx - cotx|)+C \\ &\int secxtanxdx = secx+C \\ &\int cscxcotxdx =-cscx+C \\ &\int cot^2xdx =-cscx-x+C \\ &\int \frac{1}{x^2-a^2} =\frac{1}{2a}ln|\frac{x-a}{x+a}|+C \\ &\int \frac{1}{a^2-x^2} =\frac{1}{2a}ln|\frac{x+a}{x-a}|+C \\ &\int csc^2xdx =-cotx+C \end{aligned}$