根据CART算法使用python构建决策树
前言
之前曾经实现过可以应用在离散取值区间的简易决策树,前天突发奇想仿照sklearn的实现效果写了一个取值范围可以是连续区间的通用决策树。
如果对之前的简易决策树了解不深可以先复习一下:简易决策树地址
代码介绍
依赖包
import numpy as np
from collections import Counter
from math import log2
import matplotlib.pyplot as plt
from sklearn import datasets
在这里我们为了方便直接选用了sklearn里面的数据集(仅选用数据集,算法具体实现不依赖于sklearn)。
对于依赖包的解释也可以翻阅之前的简易决策树一文。
计算损失
def entropy(y_label):
counter = Counter(y_label)
ent = 0.0
for num in counter.values():
p = num / len(y_label)
ent += -p * log2(p)
return ent
在本博客中我们选用的是信息熵,也可以选用基尼系数。
树结点
class TreeNode:
def __init__(self, acc, imin=None, minD=None):
self.acc = list(acc) # 不同类别的精度
self.imin = imin # 最小分割的特征
self.minD = minD # 分割点
树的结点中包含的信息有:在当前结点不同类别的精度、该结点损失最小分割特征、和按照损失最小分割特征分割的损失最小的分割值。
决策树类
class DecisionTree:
def __init__(self, maxentropy=1e-10, max_depth=20, min_samples=0.1):
self.tree = {}
self.maxentropy = maxentropy # 最大信息熵(分割条件:小于这个信息熵可以分割)
self.max_depth = max_depth # 递归树深度
self.min_samples = min_samples # 最小样本数
# 训练决策树
def fit(self, X, y):
if self.min_samples < 1 and self.min_samples > 0:
# 如果min_samples是小数则按照输入数据的数据量的比例确定min_samples,如果>1则给定的数值作为min_samples
self.min_samples *= len(X)
cols = list(range(X.shape[1]))
# 对X得每一列数据,计算分割后得信息熵
ylen = len(set(y))
self.tree = self._genTree(cols, X, y, ylen, 1)
# 递归生成决策树
def _genTree(self, cols, X, y, ylen, depth):
# 计算最小信息熵得特征
imin = cols[0] # 最下熵得列
leftemin = 100 # 最小左熵值
rightemin = 100 # 最小右熵值
minD = None
for i in cols:
coli = X[:, i] # 拿到第i个特征数据
sortedcoli = coli
sorted(sortedcoli)
divide = []
divide.append(coli[0])
for j in range(len(sortedcoli)):
# 划分分界线
if j == len(sortedcoli) - 1:
divide.append(sortedcoli[j])
else:
divide.append((sortedcoli[j] + sortedcoli[j+1]) / 2)
for d in divide:
# 选择不同特征的不同值所产生的最小信息熵
leftenti = entropy(y[coli < d])
rightenti = entropy(y[coli >= d])
if leftenti + rightenti < leftemin + rightemin:
imin = i
leftemin = leftenti
rightemin = rightenti
minD = d
# 求划分精度
coli = X[:, imin]
Acc = np.zeros(ylen)
leftAcc = np.zeros(ylen)
rightAcc = np.zeros(ylen)
for idx in set(y):
# print(y[coli < minD] == idx)
leftAcc[idx] = np.sum(y[coli < minD] == idx) / len(y[coli < minD])
rightAcc[idx] = np.sum(y[coli >= minD] == idx) / len(y[coli >= minD])
Acc[idx] = np.sum(y == idx) / len(y)
# print("acc:", Acc, leftAcc, rightAcc)
# 创建树
newtree = {}
# print(imin, end=":")
if leftemin < rightemin:
# 新建左叶子
Node = {}
# print(leftAcc)
Node[0] = (0, TreeNode(list(leftAcc), 0))
# print("<", minD, leftAcc, 0)
if rightemin > self.maxentropy and len(X) >= self.min_samples and depth < self.max_depth:
# 裁剪数据集
DataIndex = X[:, imin] > minD
Xcopy = X[DataIndex].copy()
ycopy = y[DataIndex].copy()
# 新建右子树
# cols.remove(imin)
Node[1] = (1, self._genTree(cols, Xcopy, ycopy, ylen, depth+1))
else:
# print(rightAcc)
Node[1] = (0, TreeNode(list(rightAcc), 0))
# print(">", minD, rightAcc, 0)
else:
# 新建右叶子
Node = {}
Node[1] = (0, TreeNode(list(rightAcc), 0))
# print(rightAcc)
if leftemin > self.maxentropy and len(X) >= self.min_samples and depth < self.max_depth:
# 裁剪数据集
DataIndex = X[:,imin] <= minD
Xcopy = X[DataIndex].copy()
ycopy = y[DataIndex].copy()
# 新建左子树
# cols.remove(imin)
Node[0] = (1, self._genTree(cols, Xcopy, ycopy, ylen, depth+1))
else:
Node[0] = (0, TreeNode(list(leftAcc), 0))
print(leftAcc)
newtree[TreeNode(list(Acc), imin, minD)] = Node
return newtree
# 预测新样本
def predict(self, X):
X = X.tolist()
# print(X)
y = [None for i in range(len(X))]
for i in range(len(X)):
tree = self.tree
while True:
node = list(tree.keys())[0] # 获取结点
acc = node.acc
imin = node.imin
minD = node.minD # 获取结点中数据
tree = tree[node] # 获取左右子节点
# print(imin)
if X[i][imin] < minD:
# 选择左节点
tree = tree[0]
if tree[0] == 0:
# 当前为叶子结点,停止查找
y[i] = np.argmax(tree[1].acc)
break
else:
tree = tree[1] # 将树根更新成右子树
else:
# 选择右节点
tree = tree[1]
if tree[0] == 0:
# 当前为叶子结点,停止查找
y[i] = np.argmax(tree[1].acc)
break
else:
tree = tree[1] # 将树根更新成右子树
return y
决策树类的代码较多,下文将按照函数详细讲解
作图函数
def plot_decision_boundary(model, X, y):
x0_min, x0_max = X[:, 0].min() - 1, X[:, 0].max() + 1
x1_min, x1_max = X[:, 1].min() - 1, X[:, 1].max() + 1
x0, x1 = np.meshgrid(np.linspace(x0_min, x0_max, 100), np.linspace(x1_min, x1_max, 100))
Z = model.predict(np.c_[x0.ravel(), x1.ravel()])
Z = np.array(Z)
Z = Z.reshape(x0.shape)
plt.contourf(x0, x1, Z, cmap=plt.cm.Spectral)
plt.ylabel('x1')
plt.xlabel('x0')
plt.scatter(X[:, 0], X[:, 1], c=np.squeeze(y))
plt.show()
按照数据集生成大量的数据并对生成的数据进行预测,画出预测结果的等高线,从而得到决策树划分结果
加载数据集
下面以make_circle、make_moons、iris为例,测试生成树的时候任选其一就行
make_circles:
X,y=datasets.make_circles(n_samples=1000,factor=0.5,noise=0.1)
make_moons:
X,y = datasets.make_moons(n_samples=500,noise=0.3,random_state=42)
iris:
iris = datasets.load_iris()
X = iris["data"][:, 2:]
y = iris["target"]
为了方便画二维图像,这里的iris数据集只选用了两个特征
主程序
if __name__ == "__main__":
# X,y=datasets.make_circles(n_samples=1000,factor=0.5,noise=0.1)
# X,y = datasets.make_moons(n_samples=500,noise=0.3,random_state=42)
iris = datasets.load_iris()
X = iris["data"][:, 2:]
y = iris["target"]
dt = DecisionTree()
dt.fit(X, y)
print(dt.tree)
print(dt.predict(X))
X = np.array(X)
y = np.array(y)
plot_decision_boundary(dt, X, y)
效果演示
make_circles数据集划分结果
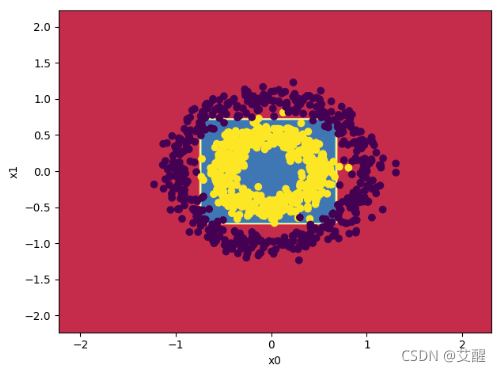
make_moons数据集划分结果
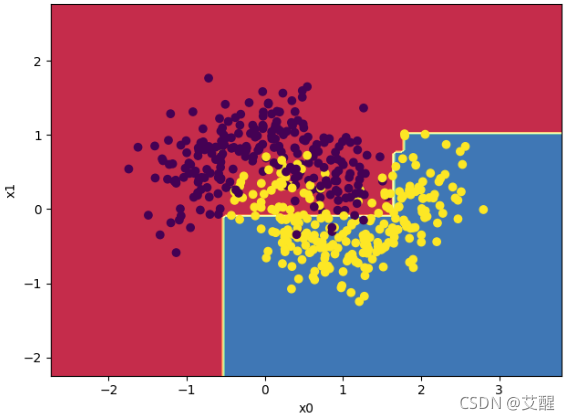
iris数据集划分结果
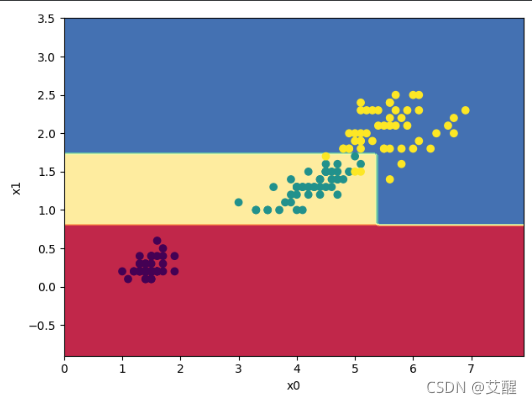
决策树类中函数解释
init 函数
def __init__(self, maxentropy=1e-10, max_depth=20, min_samples=0.1):
self.tree = {}
self.maxentropy = maxentropy # 最大信息熵(分割条件:小于这个信息熵可以分割)
self.max_depth = max_depth # 递归树深度
self.min_samples = min_samples # 最小样本数
初始化树、最大信息熵、递归树的最大深度、划分需要的最小样本数
fit函数
def fit(self, X, y):
if self.min_samples < 1 and self.min_samples > 0:
# 如果min_samples是小数则按照输入数据的数据量的比例确定min_samples,如果>1则给定的数值作为min_samples
self.min_samples *= len(X)
cols = list(range(X.shape[1]))
# 对X得每一列数据,计算分割后得信息熵
ylen = len(set(y))
self.tree = self._genTree(cols, X, y, ylen, 1)
(1)如果初始化的最小样本数min_samples<1说明min_samples表示的是最小样本数应该占总样本数的比例,应该乘以样本数获取实际最小样本数。如果初始化的最小样本数>1说明初始化的最小样本数参数即为实际最小样本数。
(2)cols代表的是每个特征的编号
(3)ylen代表数据集能够分类的最大标签数
(4)通过self._genTree函数建立决策树
_genTree函数
def _genTree(self, cols, X, y, ylen, depth):
# 计算最小信息熵得特征
imin = cols[0] # 最下熵得列
leftemin = 100 # 最小左熵值
rightemin = 100 # 最小右熵值
minD = None
for i in cols:
coli = X[:, i] # 拿到第i个特征数据
sortedcoli = coli
sorted(sortedcoli)
divide = []
divide.append(coli[0])
for j in range(len(sortedcoli)):
# 划分分界线
if j == len(sortedcoli) - 1:
divide.append(sortedcoli[j])
else:
divide.append((sortedcoli[j] + sortedcoli[j+1]) / 2)
for d in divide:
# 选择不同特征的不同值所产生的最小信息熵
leftenti = entropy(y[coli < d])
rightenti = entropy(y[coli >= d])
if leftenti + rightenti < leftemin + rightemin:
imin = i
leftemin = leftenti
rightemin = rightenti
minD = d
# 求划分精度
coli = X[:, imin]
Acc = np.zeros(ylen)
leftAcc = np.zeros(ylen)
rightAcc = np.zeros(ylen)
for idx in set(y):
# print(y[coli < minD] == idx)
leftAcc[idx] = np.sum(y[coli < minD] == idx) / len(y[coli < minD])
rightAcc[idx] = np.sum(y[coli >= minD] == idx) / len(y[coli >= minD])
Acc[idx] = np.sum(y == idx) / len(y)
# print("acc:", Acc, leftAcc, rightAcc)
# 创建树
newtree = {}
# print(imin, end=":")
if leftemin < rightemin:
# 新建左叶子
Node = {}
# print(leftAcc)
Node[0] = (0, TreeNode(list(leftAcc), 0))
# print("<", minD, leftAcc, 0)
if rightemin > self.maxentropy and len(X) >= self.min_samples and depth < self.max_depth:
# 裁剪数据集
DataIndex = X[:, imin] > minD
Xcopy = X[DataIndex].copy()
ycopy = y[DataIndex].copy()
# 新建右子树
# cols.remove(imin)
Node[1] = (1, self._genTree(cols, Xcopy, ycopy, ylen, depth+1))
else:
# print(rightAcc)
Node[1] = (0, TreeNode(list(rightAcc), 0))
# print(">", minD, rightAcc, 0)
else:
# 新建右叶子
Node = {}
Node[1] = (0, TreeNode(list(rightAcc), 0))
# print(rightAcc)
if leftemin > self.maxentropy and len(X) >= self.min_samples and depth < self.max_depth:
# 裁剪数据集
DataIndex = X[:,imin] <= minD
Xcopy = X[DataIndex].copy()
ycopy = y[DataIndex].copy()
# 新建左子树
# cols.remove(imin)
Node[0] = (1, self._genTree(cols, Xcopy, ycopy, ylen, depth+1))
else:
Node[0] = (0, TreeNode(list(leftAcc), 0))
print(leftAcc)
newtree[TreeNode(list(Acc), imin, minD)] = Node
return newtree
(1)遍历各个特征的各个分割点(分割点是按照数据集两个临近数据的均值决定),记录信息熵最小的分割特征以及其对应的分割点。
(2)求当前结点对应的每个标签的精度以及按照信息熵最小的分割特征以及其对应的分割点划分后的左节点和右节点对应的每个标签的精度。
(3)根据决策树划分的特性,每次运用得到的分割点划分后总会有一个结点可以将一部分数据完全划分出来。
(4)如果小于分割点的部分可以完全被划分出来,左子树为叶子节点。在去除小于分割点的数据之后递归建立右子树。
(5)如果大于分割点的部分可以完全被划分出来,右子树为叶子节点。在去除大于分割点的数据之后递归建立左子树。
(6)返回值是树的根节点
结点数据解释
结点的数据为一个元组,元组第0位表示该结点是叶子结点还是子树的根节点,第一位表示叶子结点或子树的根节点。
这样做的目的是为了方便使用predict函数进行预测。
predict函数
def predict(self, X):
X = X.tolist()
# print(X)
y = [None for i in range(len(X))]
for i in range(len(X)):
tree = self.tree
while True:
node = list(tree.keys())[0] # 获取结点
acc = node.acc
imin = node.imin
minD = node.minD # 获取结点中数据
tree = tree[node] # 获取左右子节点
# print(imin)
if X[i][imin] < minD:
# 选择左节点
tree = tree[0]
if tree[0] == 0:
# 当前为叶子结点,停止查找
y[i] = np.argmax(tree[1].acc)
break
else:
tree = tree[1] # 将树根更新成右子树
else:
# 选择右节点
tree = tree[1]
if tree[0] == 0:
# 当前为叶子结点,停止查找
y[i] = np.argmax(tree[1].acc)
break
else:
tree = tree[1] # 将树根更新成右子树
return y
对于每个待预测数据按照决策树每个结点的特征以及特征对应的分隔值不断遍历决策树,直到遍历到叶子结点为止。选取叶子结点中精度最高的标签作为该数据的预测结果
完整代码:
代码下载





 本文详细介绍如何用Python实现CART算法构建决策树,包括依赖包导入、信息熵计算、树结点定义、决策树类及其关键函数解读,以及通过make_circles、make_moons和iris数据集的实际应用展示。
本文详细介绍如何用Python实现CART算法构建决策树,包括依赖包导入、信息熵计算、树结点定义、决策树类及其关键函数解读,以及通过make_circles、make_moons和iris数据集的实际应用展示。


















 3692
3692












