Problem Description
Most of us know that in the game called DotA(Defense of the Ancient), Pudge is a strong hero in the first period of the game. When the game goes to end however, Pudge is not a strong hero any more.
So Pudge’s teammates give him a new assignment—Eat the Trees!
The trees are in a rectangle N * M cells in size and each of the cells either has exactly one tree or has nothing at all. And what Pudge needs to do is to eat all trees that are in the cells.
There are several rules Pudge must follow:
I. Pudge must eat the trees by choosing a circuit and he then will eat all trees that are in the chosen circuit.
II. The cell that does not contain a tree is unreachable, e.g. each of the cells that is through the circuit which Pudge chooses must contain a tree and when the circuit is chosen, the trees which are in the cells on the circuit will disappear.
III. Pudge may choose one or more circuits to eat the trees.
Now Pudge has a question, how many ways are there to eat the trees?
At the picture below three samples are given for N = 6 and M = 3(gray square means no trees in the cell, and the bold black line means the chosen circuit(s))
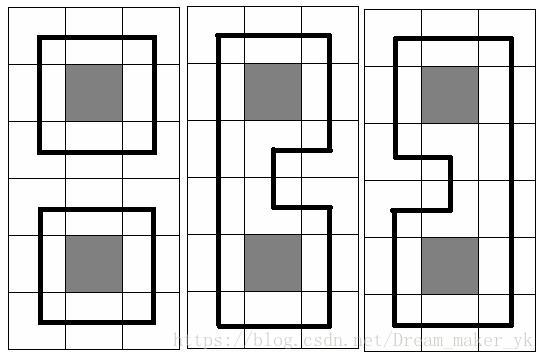
Input
The input consists of several test cases. The first line of the input is the number of the cases. There are no more than 10 cases.
For each case, the first line contains the integer numbers N and M, 1<=N, M<=11. Each of the next N lines contains M numbers (either 0 or 1) separated by a space. Number 0 means a cell which has no trees and number 1 means a cell that has exactly one tree.
Output
For each case, you should print the desired number of ways in one line. It is guaranteed, that it does not exceed 263 – 1. Use the format in the sample.
Sample Input
2
6 3
1 1 1
1 0 1
1 1 1
1 1 1
1 0 1
1 1 1
2 4
1 1 1 1
1 1 1 1
Sample Output
Case 1: There are 3 ways to eat the trees.
Case 2: There are 2 ways to eat the trees.
插头DP
可以利用异或取反的性质优化计算过程
然后写下来其实很短
#include<bits/stdc++.h>
using namespace std;
#define N 13
#define MAX (1<<13)
#define LL long long
int n,m;
int mp[N][N];
LL dp[N][N][MAX];
int main(){
int T;scanf("%d",&T);
for(int cas=1;cas<=T;cas++){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
scanf("%d",&mp[i][j]);
int up=(1<<m+1)-1;
memset(dp,0,sizeof(dp));
dp[0][m][0]=1;
for(int i=1;i<=n;i++){
for(int k=0;(k<<1)<=up;k++)dp[i][0][k<<1]=dp[i-1][m][k];
for(int j=1;j<=m;j++){
for(int k=0;k<=up;k++){//枚举上一个状态
int p=(k>>j-1)&1,q=(k>>j)&1;
if(!mp[i][j]){if(p+q==0)dp[i][j][k]+=dp[i][j-1][k];}
else{
if(p^q)dp[i][j][k]+=dp[i][j-1][k];
dp[i][j][k^((1<<j-1)|(1<<j))]+=dp[i][j-1][k];
}
}
}
}
printf("Case %d: There are %lld ways to eat the trees.\n",cas,dp[n][m][0]);
}
return 0;
}









 本文探讨了一个关于游戏DotA中英雄Pudge如何有效率地吃掉地图上的树木的问题。通过动态规划的方法,利用异或运算优化计算过程,解决了在特定地图布局下吃树的不同路径数量。
本文探讨了一个关于游戏DotA中英雄Pudge如何有效率地吃掉地图上的树木的问题。通过动态规划的方法,利用异或运算优化计算过程,解决了在特定地图布局下吃树的不同路径数量。
















 280
280

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








