本文介绍了快速排序、归并排序和堆排序三种高效的排序算法，详细阐述了它们的排序过程、代码实现、时间复杂度和空间复杂度。对于快速排序，特别讨论了最坏、最优和平均情况的时间复杂度，以及解决倒序输入的策略。归并排序和堆排序的时间复杂度均为O(nlogn)，但归并排序需要额外空间，而堆排序是就地排序。此外，文章还简要提及了堆的向下调整性质、堆排序在TopK问题的应用以及希尔排序的基本概念和时间复杂度分析。
一、排序牛B三人组
1. 快速排序
快速排序在牛B三人组中是时间最快的一个（相同情况下）。
- 取一个元素P（第一个元素），使元素P 归位。
- 列表被P分成两个部分，左边都比P小，右边都比P大。
- 递归 完成排序。
1.1 排序过程
假设一个长度为9的列表，下图中①②③④⑤⑥⑦为一个完整的归位操作，归位后列表以5为界，分成左右两个黄色的部分。
1.2 代码实现
快速排序代码关键点：归位、递归
代码思路：两个函数，一个是快排的函数，一个是归位的函数，在快排函数里调用归位函数以及递归自身(快排)。快排的终止条件是：只剩0或1个元素，因为这时肯定有序；递归的终止条件是：当left=right。取出的第一个元素要找变量存起来，不然在元素交换过程值会被覆盖掉。right是从右往左找比第一个元素小的放到左边空位，left是从左往右找比第一个元素大的放到右边空位。
import time
import random
import sys
sys.setrecursionlimit(1000000) # 把递归的最大限度改为1000000
# 计算时间装饰器：
def cal_time(func):
def inner(*args,**kwargs):
time1 = time.time()
res = func(*args,**kwargs)
time2 = time.time()
print("Time: %s" %(time2-time1))
return res
return inner
# 快速排序归位函数：
def partition(li,left,right):
temp = li[left] # 不能写li[0]，因为要递归，被存起来的元素是每个部分的第一个元素
while left < right:
while left < right and li[right] >= temp:
right -= 1
li[left] = li[right]
while left < right and li[left] <= temp:
left += 1
li[right] = li[left]
li[left] = temp
return left # partition的返回值就是元素应归位的下标
# 如果给递归函数加装饰器，里面的每次递归都会执行装饰器
def _quick_sort(li,left,right):
if left < right: # 至少有两个元素
mid = partition(li,left,right) # mid接收的是partition函数的返回值，即return left
_quick_sort(li,left,mid-1)
_quick_sort(li,mid+1,right)
# 为了统计程序运行时间，把递归函数_quick_sort放到一个不递归的函数quick_sort里
@cal_time
def quick_sort(li):
_quick_sort(li,0,len(li)-1)
在整个列表呈倒序状态时，就会出现快排的最坏情况，下面是解决办法，虽然还是无法完全解决，但降低了倒序出现的概率，并且能够应对人为把列表倒序的情况。
# 快排最坏情况解决方法：在left和right之间随机取一个数与第一个交换，避免要排序的列表是倒序
def partition1(li,left,right):
randi = random.randint(left,right)
li[randi], li[left] = li[left], li[randi]
temp = li[left]
while left < right:
while left < right and li[right] >= temp:
right -= 1
li[left] = li[right]
while left < right and li[left] <= temp:
left += 1
li[right] = li[left]
li[left] = temp
return left
1.3 时间复杂度
快排的时间复杂度分为以下三种情况：最坏情况时间复杂度，最优情况时间复杂度和平均时间复杂度。
1.3.1 最坏情况时间复杂度（O(n²)）
最坏的情况就是列表倒序想要排成正序的情况，相当于每次元素都把列表划分为一边是0个元素，一边是(n-1)个元素，所以扫描次数为：(n-1) + (n-2) + (n-3) + … + 2 + 1，根据等差数列求和公式，得扫描的总次数为：n²/2 - n/2，故快速排序时间复杂度为：O(n²)
1.3.2 最优情况时间复杂度（O(nlogn)）
递归算法的时间复杂度 = 递归次数 × 每次递归遍历的次数 。递归算法的时间复杂度公式：T[n] = aT[n/b] + f(n) 。最优情况就是每次都把列表平分成两个长度一样的子列表，此时的时间复杂度公式则为：T[n] = 2T[n/2] + f(n)。
T[n] = 2T[n/2] + n ............第1次递归
T[n] = 2[2T[n/4] + n/2] + n ............第2次递归
T[n] = 2[2[2T[n/8] + n/4] + n/2] + n ............第3次递归
= (2^3)T[n/(2^3)] + 3n
.
.
.
T[n] = (2^m)T[n/(2^m)] + mn ............第m次递归(最后一次递归T[1])
因为最后一次递归是T[1]，所以T[n/(2^m)] = T[1]，故：n/(2^m) = 1，=> m = logn
说明一共有logn层递归，并且每层递归都要扫描n次，所以快速排序的时间复杂度为：O(nlogn)
1.3.3 平均时间复杂度（O(nlogn)）
快速排序平均时间复杂度的数学推导较为复杂，可以采取一种简单的理解方式，快速排序最优情况可以看成是一个满二叉树，假设n=8：
可以想象平均情况下虽然不是满二叉树，但树还是有logn层，所以快速排序平均情况下时间复杂度还是：O(nlogn)
另外，也可以用 主定理 的方法分析快排的时间复杂度：
主定理: T [n] = aT[n/b] + f (n)
其中 a >= 1 and b > 1 是常量 并且 f (n) 是一个渐近正函数， 为了使用这个主定理，您需要考虑下列三种情况：
快速排序的每一次划分把一个问题分解成两个子问题，其中的关系可以用下式表示：
T[n] = 2T[n/2] + O(n) 其中O(n)为partition()的时间复杂度，对比主定理，
T [n] = aT[n/b] + f (n)，可以看出快速排序中：a = 2, b = 2, f(n) = O(n)，nlogba = n，属于case 2，所以快速排序的时间复杂度为：O(nlogn)
1.4 空间复杂度
首先就地快速排序使用的空间是O(1)的，也就是个常数级；而真正消耗空间的就是递归调用了，因为每次递归就要保持一些数据，占用的是栈空间，递归有多少层就占用多少栈空间：
- 最优和平均的情况下空间复杂度为：O(logn)
- 最差的情况下空间复杂度为：O(n)
2. 归并排序
归并操作：
- 申请空间，该空间用来存放合并后的序列。
- 设定两个指针，最初位置分别为两个已经 有序 序列的起始位置。
- 比较两个指针所指向的元素，选择相对小的元素放入到合并空间，并移动指针到下一位置。
- 重复步骤3直到某一指针超出序列尾，将另一序列剩下的所有元素直接复制到合并序列尾。
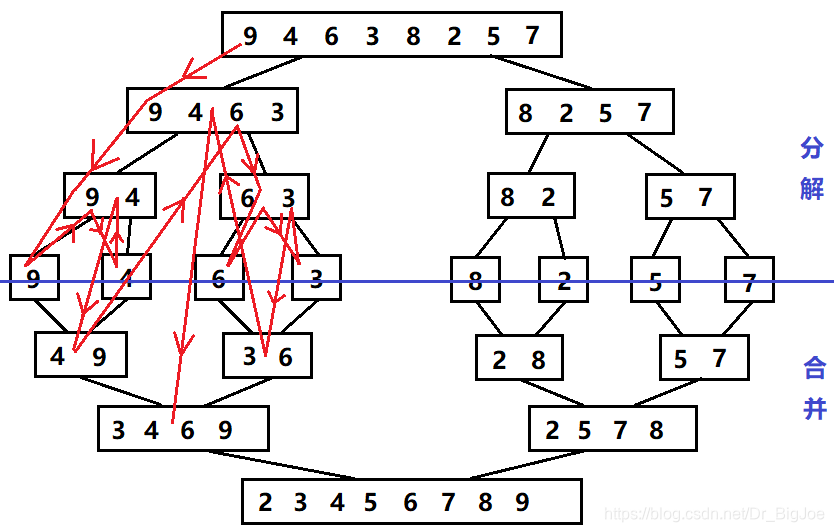
假设列表长度为9，下图①②③④⑤⑥⑦称为一次归并操作。
2.1 排序过程
- 分解：把列表越分越小直到只剩一个元素。
- 终止条件：1个元素是有序的。
- 将两个 有序 列表归并，列表越来越大。
下图绿色箭头代表merge_sort(li,low,mid)，黄色箭头代表merge_sort(li,mid+1,high)，棕色箭头代表merge(li,low,mid,high)。
下图红色箭头表示递归流程。
2.2 代码实现
归并排序代码关键点：分解、合并、终止条件
代码思路：新开辟一个列表空间用于存放合并后的列表，最后再写回原列表。两个函数，一个是归并排序的函数，一个是一次归并的函数，然后在归并排序函数中调用归并函数，并递归自身(归并排序)。分解是把列表越分越小直到只剩一个元素，因为一个元素就是有序的，也是归并排序的终止条件，合并是将两个有序列表归并，列表越来越大。归并函数除了需要low和high来表示列表的首尾元素，还需要定义i和j代表移动的指针。
# 一次归并代码：
def merge(li,low,mid,high):
# low到mid有序，mid+1到high有序
i = low
j = mid + 1
ltemp = []
while i <= mid and j <= high:
if li[i] <= li[j]:
ltemp.append(li[i])
i += 1
else:
ltemp.append(li[j])
j += 1
while i <= mid: # 右边先走完了
ltemp.append(li[i])
i += 1
while j <= high: # 左边先走完了
ltemp.append(li[j])
j += 1
li[low:high+1] = ltemp
# 归并排序代码：
def merge_sort(li,low,high):
if low < high: # 至少有两个元素
mid = (low + high)//2
merge_sort(li,low,mid)
merge_sort(li,mid+1,high)
#print(li[low:mid+1],li[mid+1:high+1])
merge(li,low,mid,high)
#print(li[low:high+1])
2.3 时间复杂度（O(nlogn)）
把一个长度为n的列表分解写到另一个列表需要n次，最后再从新列表写回原列表也需要n次，这两个过程总计2n次，所以一次归并时间复杂度不算系数为O(n)，分解时实际上每层只算一个mid值，所以分解的时间复杂度是常数级；合并时的树有logn层，也就是需要合并logn次，故归并排序的时间复杂度为：O(nlogn)
2.4 空间复杂度（O(n)）
因为归并排序需要开辟一个新的列表空间，当列表长度是n时，归并排序的空间复杂度为：O(n)
3. 堆排序
- 建立堆。
- 得到堆顶元素，为最大元素。
- 去掉堆顶，将堆最后一个元素放到堆顶(为了保证还是一个完全二叉树，只能取最后一个元素)，此时可通过一次调整重新使堆有序。
- 堆顶元素为第二大元素。
- 重复步骤3，直到堆变空。
3.1 排序过程
建立堆过程：从最后一个非叶子节点(n//2-1)开始，如下图：
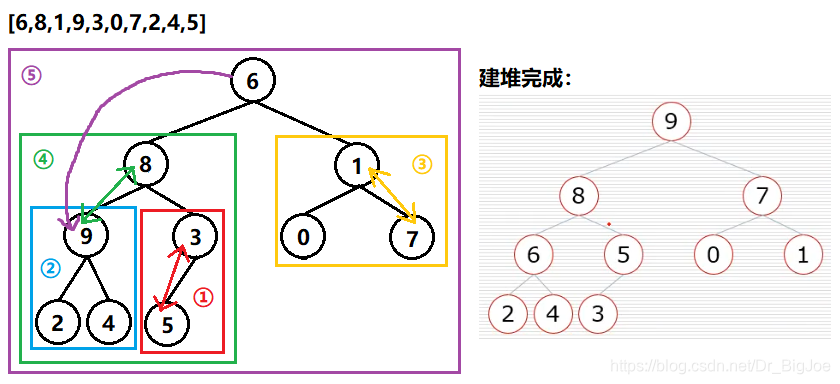
堆排序过程：如上图，根节点9是最大的，9下来，3上去根节点，然后经过一次向下调整后8在根节点；然后8下来，4上去根节点，再经过一次向下调整后7在根节点；然后7下来，2上去根节点，再经过一次向下调整后6在根节点；然后6下来，1上去根节点，再经过一次向下调整后5在根节点…以此类推，就排序完成了。需要注意的是，堆排序不需要开辟新的空间，每次下来的数就放在空的节点，只是不算做堆的一部分，不用调整了。
3.2 代码实现
堆排序代码关键点：建堆、挨个出数
代码思路：两个函数，一个是调整函数，一个是堆排函数。调整函数除了需要low和high来表示堆的首尾元素，还需要定义i和j代表移动的指针并且注意指向孩子的指针(j or j+1)都不能超过high。堆排函数分为两步：1.建堆：从最后一个非叶子节点开始，倒着循环每个节点直到根节点，循环的每一个子树都需要sift。2.挨个出数：从最后一个元素倒着循环，将最后一个元素和最顶元素互换，每次换完对剩余元素sift。
# 一次调整代码：
def sift(li,low,high):
"""
:param li:
:param low: low表示当前要调整的子树的根节点
:param high: high表示整个堆的最后一个元素
:return:
"""
temp = li[low]
i = low
j = 2*i + 1
while j <= high: # 退出条件2：当前i位置是叶子节点，j位置超过了high
# j指向更大的孩子
if j+1 <= high and li[j+1] > li[j]:
j = j + 1 # 如果右孩子存在并且是两个孩子之中最大的，j指向右孩子
if temp < li[j]:
li[i] = li[j]
i = j
j = 2*i + 1
else: # 退出条件1：temp值大于两个孩子的值
break
li[i] = temp
# 堆排序代码：
def heap_sort(li):
# 1. 建堆
n = len(li)
# 长度为n的列表，排成二叉树，树最后一个元素为n-1，已知孩子节点找父节点是(i-1)//2
# 故将n-1带入i得：最后一个非叶子结点下标为：n//2 -1
for i in range(n//2-1,-1,-1):
# i 是建堆时要调整的子树的根的下标
sift(li,i,n-1)
# 2. 挨个出数
for i in range(n-1,-1,-1): # i表示当前的high值，也表示即将上去的元素的位置
li[i],li[0] = li[0],li[i]
# 现在堆的范围: 0 ~ i-1
sift(li,0,i-1)
3.3 时间复杂度（O(nlogn)）
堆排序的时间复杂度，主要在建堆过程和调整过程。
（1）建堆过程：假如有n个节点，那么高度为H=logn，最后一层每个父节点最多只需要下调1次，倒数第二层最多只需要下调2次，顶点最多需要下调H次，而最后一层父节点共有2^(H-1) 个,倒数第二层共有2^(H-2) 个，顶点只有2^0个，所以总共的时间复杂度为：
H = log2(n) => n = 2^H
S = 1*2^(H-1)+2*2^(H-2)+...+(H-1)*2^1+H*2^0
= 1*n/(2^1)+2*n/(2^2)+...+(log2(n)-1)*n/(2^[log2(n)-1])+log2(n) (1)
2S = n+2*n/(2^1)+3*n/(2^2)+...+(log2(n)-1)*n/(2^[log2(n)-1])+2log2(n) (2)
(2)-(1)得：
S = n + n/(2^1) + n/(2^2) +...+ n/(2^[log2(n)]) + n/(2^[log2(n)-1])-log2(n)
= n + n[1/(2^1)+1/(2^2)+...+1/(2^[log2(n)])+1/(2^[log2(n)-1])] -log2(n)
设 1/(2^1)+1/(2^2)+...+1/(2^[log2(n)])+1/(2^[log2(n)-1]) 为f(n)，
由等比数列求和公式得：
f(n) = 1/2 * ([1- (1/2)^[log2(n)-1]] / [1-(1/2)])
= 1- (1/2^[log2(n)-1]) 括号内分子分母同乘2
= 1- (2/n)
将f(n)带入S得：
S = n + n(1- (2/n)) - log2(n)
= 2n-2-log2(n)
故建堆过程的时间复杂度为：O(n)
（2）调整过程：每次都是从根节点往下比较，n个元素需要比较n-1次，每一次最多比较logn层，故调整过程时间复杂度为：(n-1)*logn = nlogn - logn => O(nlogn)
综上所述，堆排序的时间复杂度为：O(nlogn)+O(n) => O(nlogn)
3.4 空间复杂度（O(1)）
因为堆排序是就地排序，所以空间复杂度为：O(1)
二、排序补充
1. 树与二叉树简介
- 树是一种数据结构。比如：目录结构。
- 树是一种可以递归定义的数据结构。
- 树是由n个节点组成的集合：
如果n=0，那这是一棵空树；
如果n>0，那存在一个节点作为树的根节点，其他节点可以分为m个集合，每个集合本身又是一棵树。 - 二叉树：度不超过2的树（节点最多有两个叉）。
- 满二叉树：一个二叉树，如果每一个层的节点数都达到最大值，则这个二叉树就是满二叉树。
- 完全二叉树：叶节点只能出现在最下层和次下层，并且最下面一层的节点都集中在该层最左边的若干位置的二叉树。
- 二叉树的其中一种存储方式：顺序存储方式(列表)
- 父节点下标与左孩子节点下标关系：假设父节点下标为i，左孩子节点下标为 2i+1。
- 父节点下标与右孩子节点下标关系：假设父节点下标为i，右孩子节点下标为 2i+2。
- 孩子节点下标和父节点下标关系：假设孩子节点下标为i，父节点下标为 (i-1)//2。
2. 堆
- 大根堆：一棵完全二叉树，满足任一节点都比其孩子节点大。
- 小根堆：一棵完全二叉树，满足任一节点都比其孩子节点小。
2.1 堆的向下调整性质
假设节点的左右子树都是堆，但自身不是堆。
当根节点的左右子树都是堆时，可以通过一次向下调整来将其变换成一个堆。下图①②③④为一个完整的向下调整。
3. 堆排序应用（TopK问题）
现在有n个数，设计算法找出前k大的数(k<n)。
- 排序后切片：时间复杂度：O(nlogn+k)
- 冒泡排序冒k次泡：时间复杂度：O(nk)
- 选择排序选k次：时间复杂度：O(nk)
- 插入排序限定列表长度为k，选前k大的，小的舍弃(不放在列表中)，比较需要n次，每趟挪牌只需要k次，所以时间复杂度：O(nk)
- 堆排序取前k大：时间复杂度：O(nlogk)，具体方法见下图：
堆排序取前k大代码实现：
# 堆排序求前k大代码：
def sift(li,low,high):
"""
:param li:
:param low: low表示当前要调整的子树的根节点
:param high: high表示整个堆的最后一个元素
:return:
"""
temp = li[low]
i = low
j = 2*i + 1
while j <= high: # 退出条件2：当前i位置是叶子节点，j位置超过了high
# j指向更大的孩子
if j+1 <= high and li[j+1] < li[j]: # 要建立小根堆
j = j + 1 # 如果右孩子存在并且是两个孩子之中最大的，j指向右孩子
if temp > li[j]:
li[i] = li[j]
i = j
j = 2*i + 1
else: # 退出条件1：temp值大于两个孩子的值
break
li[i] = temp
def topK(li,k):
heap = li[0:k]
for i in range(k//2-1,-1,-1): # 建堆
sift(heap,i,k-1)
for i in range(k,len(li)): # 遍历列表元素
if li[i] > heap[0]: # li[i]如果比堆顶大，那么现在的堆顶heap[0]肯定不是前k大的数，就用li[i]顶替掉heap[0]
heap[0] = li[i]
sift(heap, 0, k - 1)
for i in range(k-1,-1,-1): # 挨个出数
heap[0],heap[i] = heap[i],heap[0]
sift(heap,0,i-1)
return heap
4. 希尔排序
- 希尔排序是一种分组插入排序算法。
- 首先取一个整数d1 = n/2，将元素分为d1个组，每组相邻两元素之间距离为d1，在各组内进行直接插入排序。
- 取第二个整数d2 = d1/2，重复上述分组排序过程，直到di = 1，即所有元素在同一组内进行直接插入排序。
- 希尔排序每趟并不是某些元素有序，而是使整体数据越来越接近有序，最后一趟排序使得所有数据有序。
- 希尔排序是非稳定排序。
4.1 排序过程
假设列表长度为9。
4.2 代码实现
希尔排序代码关键点：gap、分组插入
代码思路：两个函数，一个是分组插入函数，一个是希尔排序函数，且在希尔排序函数中调用分组插入函数。分组插入的代码和插入排序类似，只是每张牌之间不是+1-1的关系而是+gap-gap的关系。希尔排序的终止条件就是间隔gap小于0。
# 一次分组插入：
def insert_sort_gap(li,gap):
for i in range(1,len(li)): # i是摸到牌的下标
temp = li[i]
j = i - gap # j是手里最后一张牌的下标
# 两个终止条件顺序不能乱，因为布尔运算有短路功能
while j >= 0 and li[j] > temp: # j小于0表示temp是最小的
li[j+gap] = li[j]
j -= gap
li[j+gap] = temp
# 希尔排序：
def shell_sort(li):
d = len(li) // 2
while d > 0:
insert_sort_gap(li,d)
d = d // 2
4.3 时间复杂度
希尔排序的时间复杂度讨论比较复杂，并且与选取的gap有关。
4.4. 空间复杂度（O(1)）
希尔排序的空间复杂度为：O(1)
三、排序总结
稳定性指的是在排序的过程中，两个相等的元素的相对位置不会改变。
上图中的排序凡是挨着交换的就是稳定排序，凡是飞着交换的就是不稳定排序。
================================================================
参考文献：
https://www.cnblogs.com/pugang/archive/2012/07/02/2573075.html
本篇涉及代码见week17
扫一扫
3300
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
