目录
一 概述
和线性表相比,栈也存在两种储存结构,一种是顺序储存,一种是链式储存。各自的优缺点和顺序表与链表一致。
栈的特点是先进后出。这种数据结构相较于一般的顺序表来说,实现了一些简化,同时在功能上存在一定的限制,但是对于特定环境的问题解决具有奇效。
二 代码
2.1 结构体&&宏定义
#include <stdio.h>
#include <stdlib.h>
#define MAX 5
#define OK 1
#define ERROR 0
typedef struct Stack
{
int top;
int data[MAX];
} IntStack, *IntStackPtr;一贯的风格,MAX,OK,ERROR的宏定义。
2.2 栈的初始化
IntStackPtr Init()
{
IntStackPtr My_Stack;
My_Stack = (IntStackPtr)malloc(sizeof(IntStack));
My_Stack->top = -1;
return My_Stack;
}栈初始化需要注意的是把top置为-1.
2.3 压栈
int Push(IntStackPtr My_List, int e)
{
if (My_List->top > MAX - 2)
{
printf("已经达到满栈!\n");
return ERROR;
}
IntStackPtr p, q, r;
p = My_List;
p->top++;
p->data[p->top] = e;
return OK;
}有时候,无论是栈还是链表或者是后面要学习的其他数据结构,我们都应该对这个数据结构进行一个初始说明,比如在栈中,我们需要表明,这个栈的TOP指向的元素是否是一个有意义的元素。在老师的代码中,我也比较认可这种写法,Top指向的那个元素就是数组中有效的栈顶元素,但是有的代码Top指向的是栈顶元素的再上一个元素。在写法上的区别是先top++还是先赋值。
2.4 出栈
int Pop(IntStackPtr My_Stack, int *e)
{
if (My_Stack->top == -1)
{
printf("已经达到栈底!\n");
return ERROR;
}
My_Stack->top--;
*e=My_Stack->data[My_Stack->top+1];
return OK;
}2.5 栈元素的打印
int PrintStack(IntStackPtr My_Stack)
{
for (int i = 0; i <= (My_Stack->top); i++)
{
printf("%d ", My_Stack->data[i]);
}
printf("\n");
return OK;
}2.6 测试代码
int main()
{
IntStackPtr My_Stack = Init();
Push(My_Stack, 1);
Push(My_Stack, 2);
Push(My_Stack, 3);
Push(My_Stack, 4);
Push(My_Stack, 5);
Push(My_Stack, 6);
PrintStack(My_Stack);
int *e;
Pop(My_Stack,e);
printf("Pop_Result:%d\n",*e);
Pop(My_Stack,e);
printf("Pop_Result:%d\n",*e);
Pop(My_Stack,e);
printf("Pop_Result:%d\n",*e);
Pop(My_Stack,e);
printf("Pop_Result:%d\n",*e);
Pop(My_Stack,e);
printf("Pop_Result:%d\n",*e);
return 0;
}实现Pop和Push功能的时候,加入了一些合理性检验的内容,比如,压栈的时候判断是否达到了栈顶,出栈的时候,是否已经在栈底,Top为-1。在main函数检测的时候加入了这些内容。
2.7 运行结果
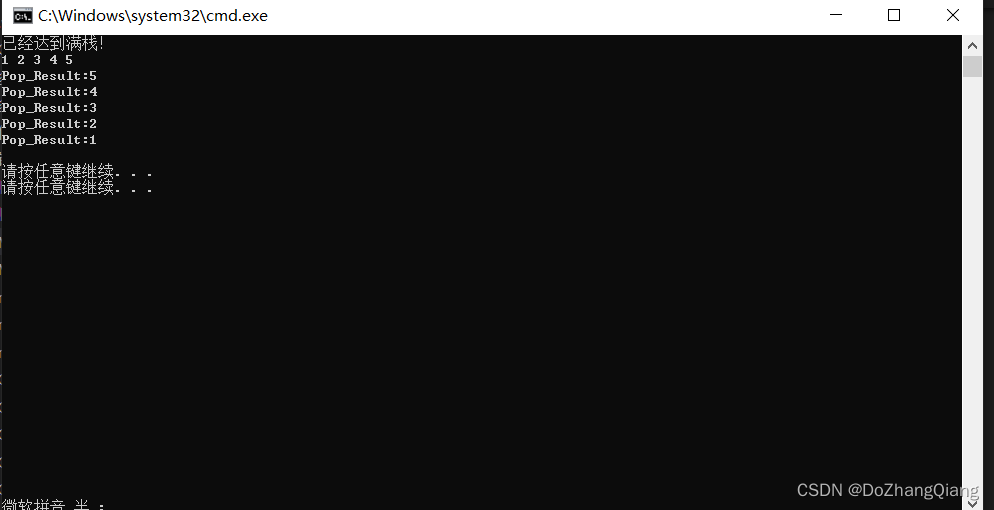
三 顺序栈总结&反思
顺序栈还是比较简单的,栈的难点在于他的应用上面(运算的那个算法真的听的糊里糊涂的),关键是用到了他先进后出的特点。
在栈数据结构的问题里面,需要注意赋值与top数变化的先后顺序,这里不要搞错。
上课的时候也有提到链栈,链式储存的好处自然是可以充分地利用空间,数量不受限制,但是写的时候相对麻烦一些,他不能像顺序表那样,通过下标的--来得到上一个元素,而是需要多储存一次指针,通过指针的回溯来去访问。
四 括号匹配的应用
栈的一个典型应用式括号的匹配判断以及进一步的四则运算算法。括号的匹配算法还式相对简单一点的,在这篇博客里面顺便就讲啦。
本质是在上述Pop和Push函数的基础上加一个基于switch的应用函数。
4.1 代码
int bracketMatching(char *My_String, int length)
{
IntStackPtr tempStack = Init();
Push(tempStack, '#');
char tempElem;
char temp_Ele;
for (int i = 0; i < length; i++)
{
tempElem = My_String[i];
switch (tempElem)
{
case '(':
case '[':
case '{':
Push(tempStack, tempElem);
break;
case ')':
Pop(tempStack, &temp_Ele);
if (temp_Ele != '(')
{
return 0;
}
break;
case ']':
Pop(tempStack, &temp_Ele);
if (temp_Ele != '[')
{
return 0;
}
break;
case '}':
Pop(tempStack, &temp_Ele);
if (temp_Ele != '{')
{
return 0;
}
break;
default:
break;
}
}
return 1;
}在老师的基础上做了一些修改,比如整个for循环之后,老师有一个判断是否为'#'的操作,我去做了几个测试样例,把这一步省略是没有影响的。因为在switch的时候,如果Push出的元素无法进行正确的匹配 自然会return 0了。即使是极端测试样例,“)”最后的结果也是不影响的。
4.2 测试样例
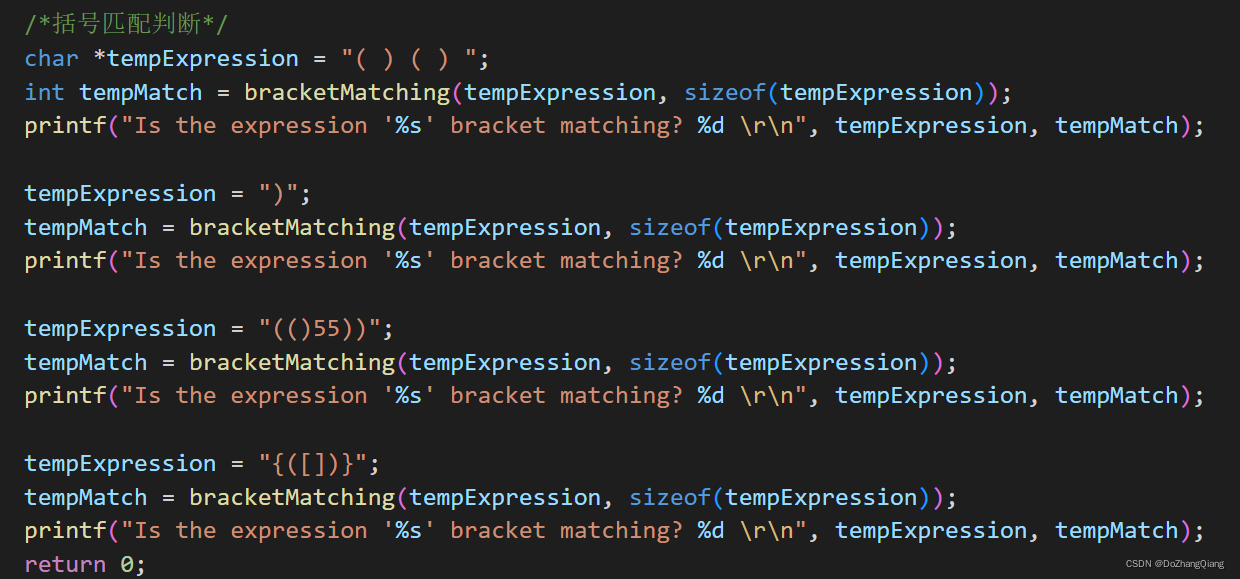
4.3 运行结果
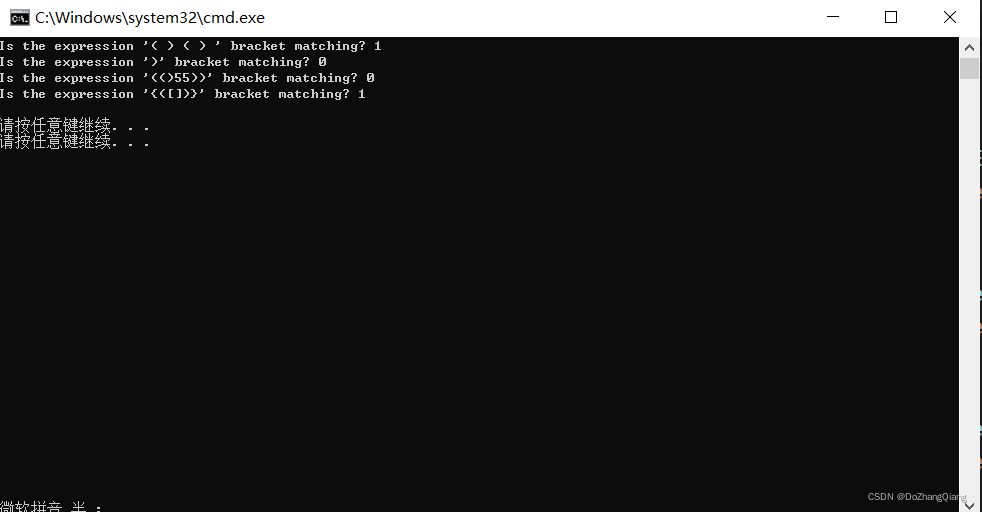
5.括号匹配总结&反思
匹配算法中,我觉得核心的几个点,首先是左括号类别的case,需要去进行压栈,然后break。其次是右括号的类别,需要要进行Pop当前的栈顶去进行匹配Judge。其他地方就没有什么了,对了,在传入函数字符串长度的时候,可以进行一手strlen函数。




 本文详细介绍了如何使用C语言实现顺序栈,包括结构体定义、初始化、压栈、出栈、打印栈元素等功能,并通过括号匹配问题展示了栈的实际应用。通过测试代码和运行结果,阐述了栈在解决特定问题时的高效性和实用性。
本文详细介绍了如何使用C语言实现顺序栈,包括结构体定义、初始化、压栈、出栈、打印栈元素等功能,并通过括号匹配问题展示了栈的实际应用。通过测试代码和运行结果,阐述了栈在解决特定问题时的高效性和实用性。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








