系列文章目录
- leetcode - 双指针问题_leetcode双指针题目-优快云博客
- leetcode - 滑动窗口问题集_leetcode 滑动窗口-优快云博客
- 高效掌握二分查找:从基础到进阶-优快云博客
- leetcode - 前缀和_前缀和的题目-优快云博客
- 动态规划 - 斐波那契数列模型-优快云博客
- 位运算 #常见位运算总结 #题解-优快云博客
- 模拟 - #介绍 #题解-优快云博客
- leetcode - 分治-三路划分快速排序总结-优快云博客
- 动态规划 - 路径问题-优快云博客
- 动态规划 - 简单多状态 dp 问题-优快云博客
目录
前言
路漫漫其修远兮,吾将上下而求索;
大家可以提前做一下:
- 53. 最大子数组和 - 力扣(LeetCode)
- 918. 环形子数组的最大和 - 力扣(LeetCode)
- 152. 乘积最大子数组 - 力扣(LeetCode)
- 1567. 乘积为正数的最长子数组长度 - 力扣(LeetCode)
- 413. 等差数列划分 - 力扣(LeetCode)
- 978. 最长湍流子数组 - 力扣(LeetCode)
- 139. 单词拆分 - 力扣(LeetCode)
- 467. 环绕字符串中唯一的子字符串 - 力扣(LeetCode)
1、题1 最大子数组和:
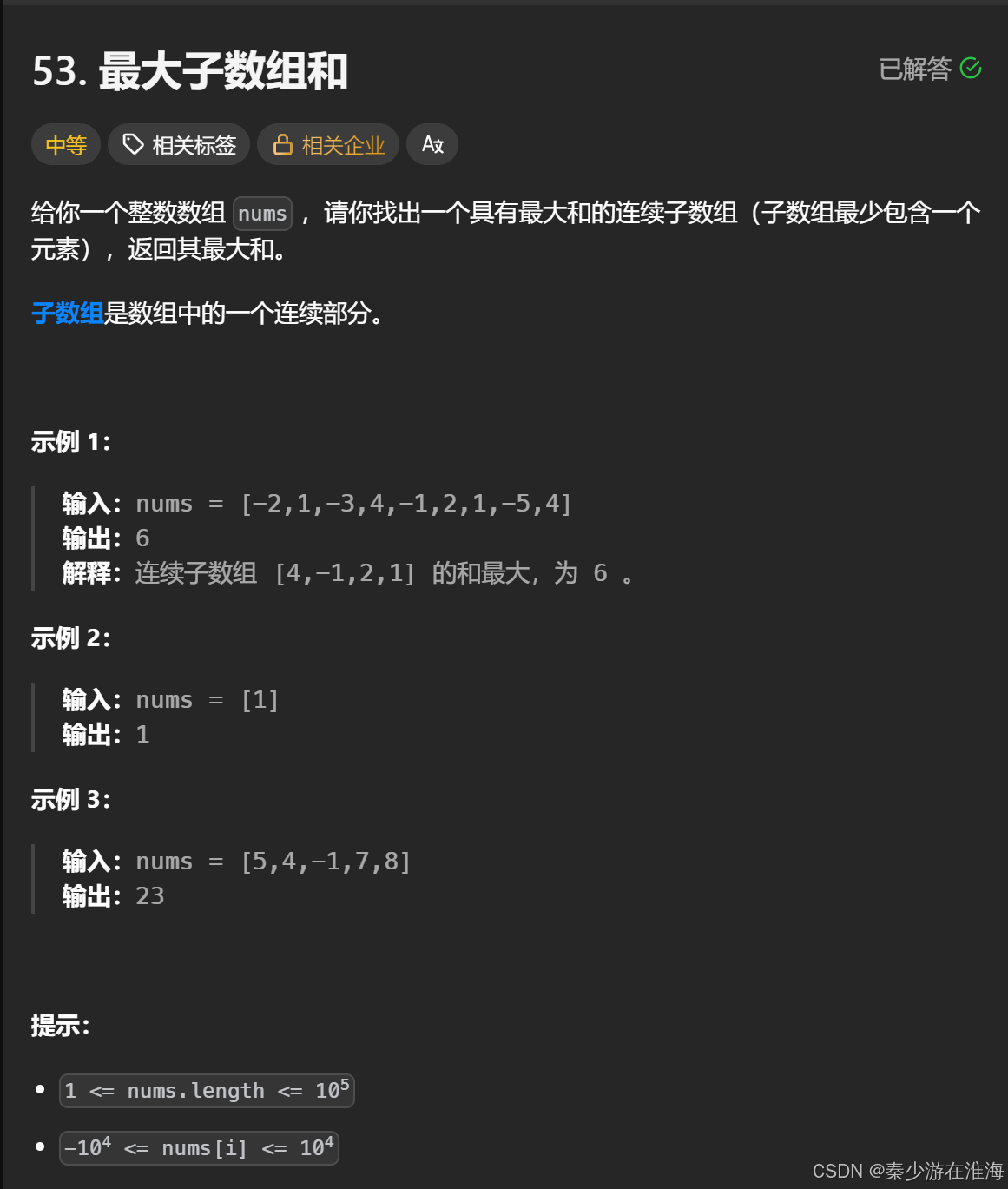
梳理:在nums 中找到和最大的连续区间;
动规五部曲:1、确定状态表达式; 2、状态转移方程;3、初始化; 4、填表顺序;5、返回值
1.1 确定状态表示
状态表示的确定一般是以某一个位置为结尾,或者是以某一个位置为起点;
根据题干以及经验,dp[i]表示:以i 位置为结尾的所有子数组中的最大和;
1.2 状态转移方程
以 i 位置为结尾的所有子数组可以分为两类,一类是单独的 nums[i](长度等于1) ,一类是nums[i] 与其前面的元素相结合组成的区间(长度大于1);
那么 :

取这两种情况的最大值就行,即dp[i] = max(nums[i] , dp[i-1]+nums[i]);
1.3 初始化
观察我们的状态转移方程就可以发现,当 i 为0的时候,下标不合法,我们就需要初始化 dp[0];当 i 为0 的时候,长度就只能为1,所以dp[0] = nums[0];
当然,还有一种处理方式:为 dp表多开辟一个空间,但是需要注意的是需要注意虚拟结点中的值要保证填表是正确的,以及下标的映射关系;多开辟一个空间来处理,dp[0] = 0;
1.4 填表顺序
确定填表顺序的目的是为了填写当前状态值时所依赖的前一个状态是已经确定的,观察我们的状态转移方程,在填写dp 表第 i 个时,需要依赖dp 表中 i-1 的数据,所以填表顺序为从左往右;
1.5 返回值
结合题干:![]()
因为最大和区间的位置不确定,返回dp表中最大值即可;
参考代码1:
int maxSubArray(vector<int>& nums)
{
int n = nums.size();
vector<int> dp(n);
//初始化
dp[0] = nums[0];
//填表
int ret = dp[0];
for(int i = 1;i<n;i++)
{
dp[i] = max(nums[i] , nums[i] +dp[i-1]);
ret = max(ret , dp[i]);
}
return ret;
}多开辟一个空间:
参考代码2:
int maxSubArray(vector<int>& nums)
{
int n = nums.size();
vector<int> dp(n+1);
//初始化
dp[0] = 0;
//填表
int ret = INT_MIN;
for(int i = 1;i<=n;i++)
{
dp[i] = max(nums[i-1] , nums[i-1] +dp[i-1]);//注意下标的映射关系
ret = max(ret , dp[i]);
}
return ret;
}2、题2 环形子数组的最大和:

Q:如何处理环形数组?
- 在打家劫舍2 之中,通过分情况讨论我们将环形数组转换成了普通的数组,然后在普通数组上用之前学过的知识来解决;
此处也可以分情况讨论,在本题中非空子数组有两种情况:
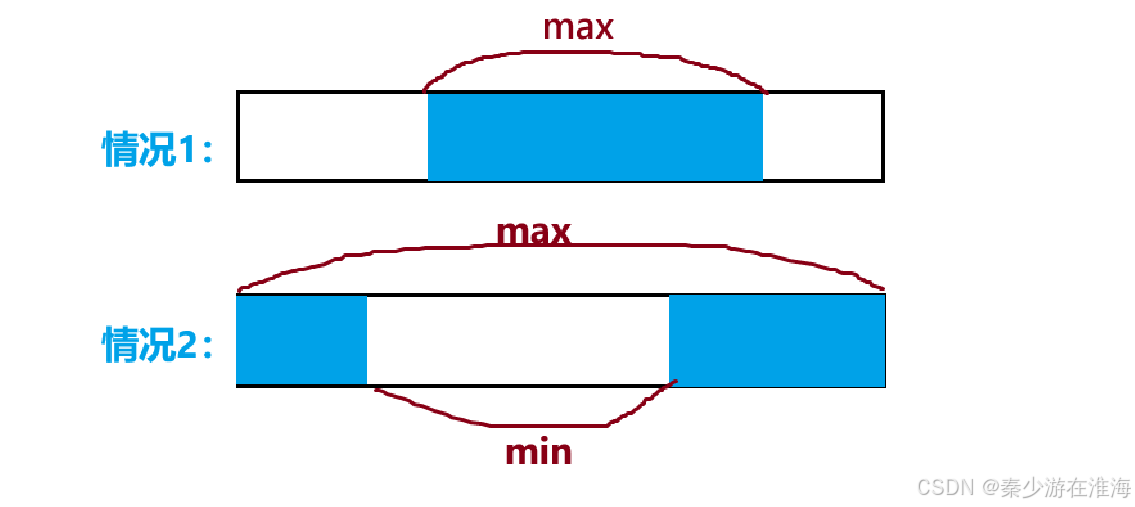
2.1 确定状态表示
状态表示一般是以某一个位置为结尾,或者是以某一个位置为起始;
我们此处需要利用两个dp 表,一个用来查找以i位置结尾的最大和,一个用来查找以i 为结尾的最小和;
f[i] 表示: 以 i 位置为结尾的所有子数组中的最大和
g[i]表示: 以 i 位置为结尾的所有子数组中的最小和
2.2 状态转移方程
对于 f[i] 来说,当走到 i 位置的时候,可以分为两种情况,一个是该以i 位置结束的区间只有一个数据,二是以 i 为结束的区间中的数据大于1,取这两种情况的最大值即可,即 f[i] = max(nums[i], f[i-1]+nums[i]);
对于 g[i] 来说,当走到 i 位置的时候,可以分为两种情况,一个是该以i 位置结束的区间只有一个数据,二是以 i 为结束的区间中的数据大于1,取这两种情况的最小值即可,即g[i] = min(nums[i] , g[i-1] + nums[i]);
2.3 初始化
观察我们的状态转移方程,当 i 为0 的时候,两个dp表均会发成越界,所以我们需要初始化 f[0]、g[0] ;当 i 为0时,对于 f[0] 意味着以下标为0结尾区间的最大值,因为只有一种情况:长度为1,所以 f[0] = nums[0]; 对于 g[0] 意味着以下标为0为结尾区间的最小值,因为只有一种情况:长度为1,所以g[0] = nums[0];
当然了,还有一种处理方式,可以为这两个 dp 表多开辟一个空间,但是需要注意虚拟节点中的值需要保证后面填表的正确性以及下标的映射关系;因为 f[i] = max(nums[i], f[i-1]+nums[i]) , 不影响其填表即 f[0] = 0;因为g[i] = min(nums[i] , g[i-1] + nums[i]) , 不影响其填表,即g[0] = 0;
2.4 填表顺序
确定填表顺序是为了保证我们填写当前状态时所依赖的状态是已经知道的,观察状态转移方程,当我们填写第 i 个位置的时候,依赖第 i-1 位置上的数据,所以我们的填表顺序为从左往右;
2.5 返回值
结合题干:![]()
找到 f 表中的最大值以及g 表中的最小值(还需要将 g表中的最小值通过计算间接得到 nums 中的最大和),在这两种情况种取最大值返回即可;
其中需要注意的是,当nums 中全为负数的时候,直接返回 f 表中的最大值, 因为g 表中的最小值一定为nums 中所有的数据之和,而与nums 中所有数据和相等,那么计算出来区间长度为0,和为0这种情况是不存在的;
参考代码1:
int maxSubarraySumCircular(vector<int>& nums)
{
int n = nums.size();
vector<int> f(n),g(n);
//初始化
f[0] = nums[0],g[0] = nums[0];
//填表
int maxi = f[0] , mini = g[0], sum = nums[0];
for(int i = 1 ;i<n;i++)
{
f[i] = max(nums[i] , f[i-1]+nums[i]);
g[i] = min(nums[i] , g[i-1]+nums[i]);
maxi = max(maxi , f[i]);
mini = min(mini , g[i]);
sum += nums[i];
}
//全为负数,直接返回 maxi
return sum == mini ? maxi : max(maxi , sum - mini);
}当然也可以为两个dp 表多开辟一个空间:
参考代码2:
int maxSubarraySumCircular(vector<int>& nums)
{
int n = nums.size();
vector<int> f(n+1),g(n+1);
//填表
int maxi = INT_MIN , mini = INT_MAX, sum = 0;
for(int i = 1 ;i<=n;i++)
{
//注意下标的映射关系
f[i] = max(nums[i-1] , f[i-1]+nums[i-1]);
g[i] = min(nums[i-1] , g[i-1]+nums[i-1]);
maxi = max(maxi , f[i]);
mini = min(mini , g[i]);
sum += nums[i-1];
}
//全为负数,直接返回 maxi
return sum == mini ? maxi : max(maxi , sum - mini);
}3、题3 乘积最大子数组:

3.1 确定状态转移返程:
状态表示一般是以某一个位置为结尾,或者是以某一个位置为起始;
根据题干以及经验,dp[i]表示:以i 位置为结尾的所有子数组中的最大乘积;先看此状态表示能否推导出状态转移方程,如果能推出来就说明该状态表示是正确的,如果不能就需要重新确定状态表示;
3.2 状态转移方程
以 i 位置为结尾的所有子数组可以分为两类,一类是单独的 nums[i](长度等于1) ,一类是nums[i] 与其前面的元素相结合组成的区间(长度大于1);
那么:

但此处的nums[i] 可能为负数,就需要乘以 [0,i-1] 区间中乘积最小的;如果nums[i] 为正数,就需要乘以 [0,i-1] 区间中乘积最大的;故而此处我们需要两个dp表:
f[i] 表示: 以 i 位置为结尾的所有子数组中的最大乘积
g[i] 表示:以 i 位置为结尾的所有子数组中的最小乘积
所以正确的状态转移方程应该是:

当nums[i] 为0 的时候不会影响结果,所以此处并没有讨论当 nums[i] 为0的情况;
3.3 初始化
观察我们的状态转移方程,当 i 为0 的时候,两个dp表均会发成越界,所以我们需要初始化 f[0]、g[0] ;当 i 为0时,对于 f[0] 意味着以下标为0结尾区间的最大乘积,因为只有一种情况:长度为1,所以 f[0] = nums[0]; 对于 g[0] 意味着以下标为0为结尾区间的最小值,因为只有一种情况:长度为1,所以g[0] = nums[0];
当然了,还有一种处理方式,可以为这两个 dp 表多开辟一个空间,但是需要注意虚拟节点中的值需要保证后面填表的正确性以及下标的映射关系;因为 f[i] = max(nums[i], f[i-1]*nums[i] ,g[i-1]*nums[i]) , 不影响其填表即 f[0] = 1;因为g[i] = min(nums[i] , g[i-1] + nums[i] , f[i-1]*nums[i]) , 不影响其填表,即g[0] = 1;
3.4 填表顺序
确定填表顺序是为了保证我们填写当前状态时所依赖的状态是已经知道的,观察状态转移方程,当我们填写第 i 个位置的时候,依赖第 i-1 位置上的数据,所以我们的填表顺序为从左往右,并且两个表需要同时填写;
3.5 返回值
返回 f 表中的最大值
参考代码1:
int maxProduct(vector<int>& nums)
{
int n = nums.size();
vector<int> f(n) ,g(n);
//初始化
f[0] = nums[0] , g[0] = nums[0];
//填表
int ret = f[0];
for(int i = 1;i<n;i++)
{
//两个表同时填写
f[i] = max(nums[i],max(f[i-1]*nums[i] , g[i-1]*nums[i]));
g[i] = min(nums[i] , min(g[i-1]*nums[i] , f[i-1]*nums[i]));
ret = max(ret ,f[i]);
}
return ret;
}当然也可以为两个dp 表多开辟一个空间:
参考代码2:
int maxProduct(vector<int>& nums)
{
int n = nums.size();
vector<int> f(n+1) ,g(n+1);
//初始化
f[0] = g[0] = 1;
//填表
int ret = INT_MIN;
for(int i = 1;i<=n;i++)
{
//两个表同时填写,注意下标的映射关系
f[i] = max(nums[i-1],max(f[i-1]*nums[i-1] , g[i-1]*nums[i-1]));
g[i] = min(nums[i-1] , min(g[i-1]*nums[i-1] , f[i-1]*nums[i-1]));
ret = max(ret ,f[i]);
}
return ret;
}4、题4 乘积为正数的最长子数组长度:
1567. 乘积为正数的最长子数组长度 - 力扣(LeetCode)
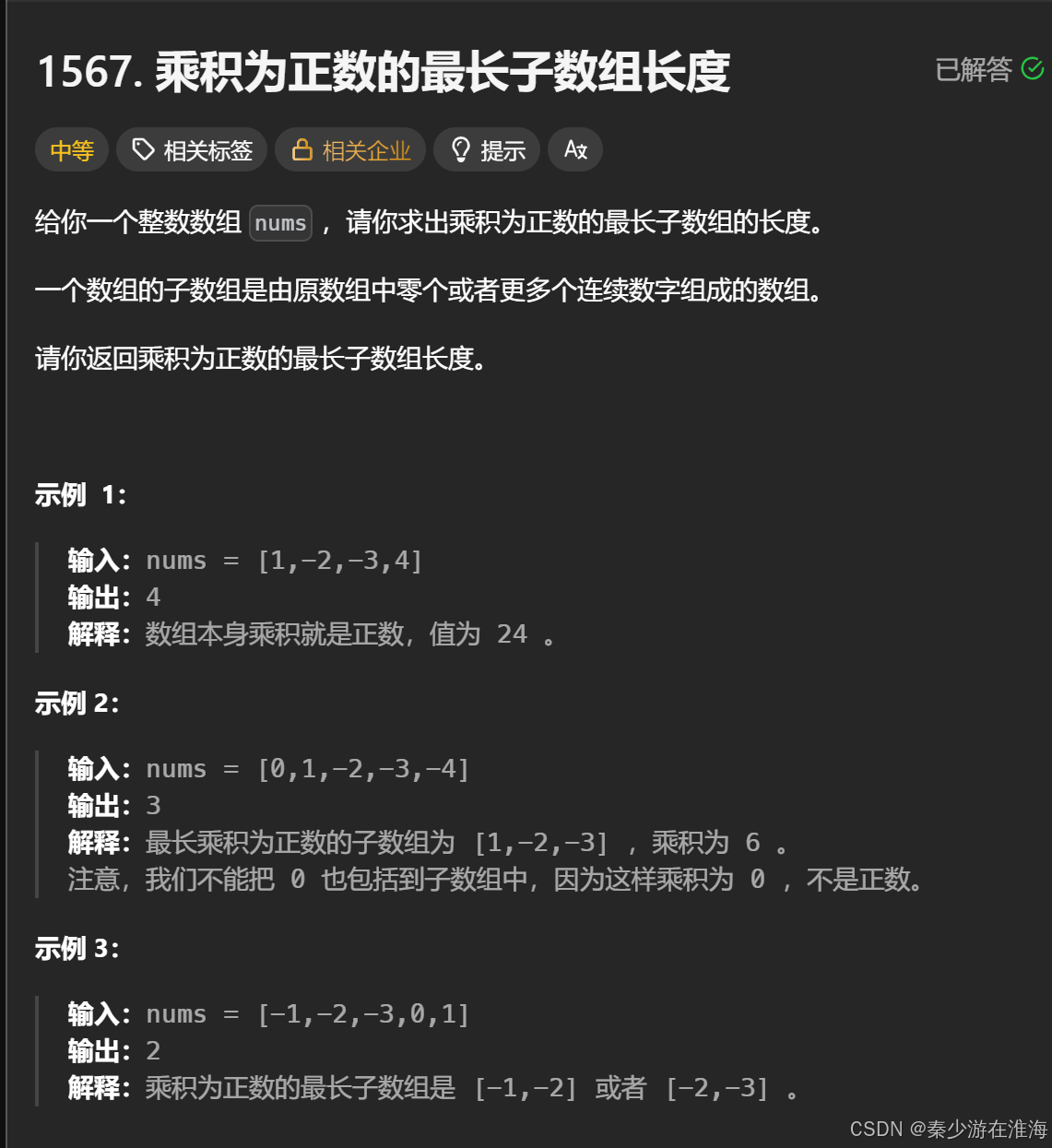
需要注意的是此处子数组的长度可以为0;
4.1 确定状态表示
状态表示一般是以某一个位置为结尾,或者是以某一个位置为起始;
根据题干以及经验,做了上一题,做这道题的时候就必定会知道,本题需要两个dp 表,一个dp 表用来记录乘积为正数的最大长度,一个dp 表用来记录乘积为负数的最大长度;
f[i] 表示: 以 i 位置元素为结尾的所有子数组中乘积为正数的最长长度
g[i] 表示:以 i 位置元素为结尾的所有子数组中乘积为负数的最长长度
4.2 状态转移方程
同样地,可以划分为两种情况来进行讨论:长度为1,长度大于1;
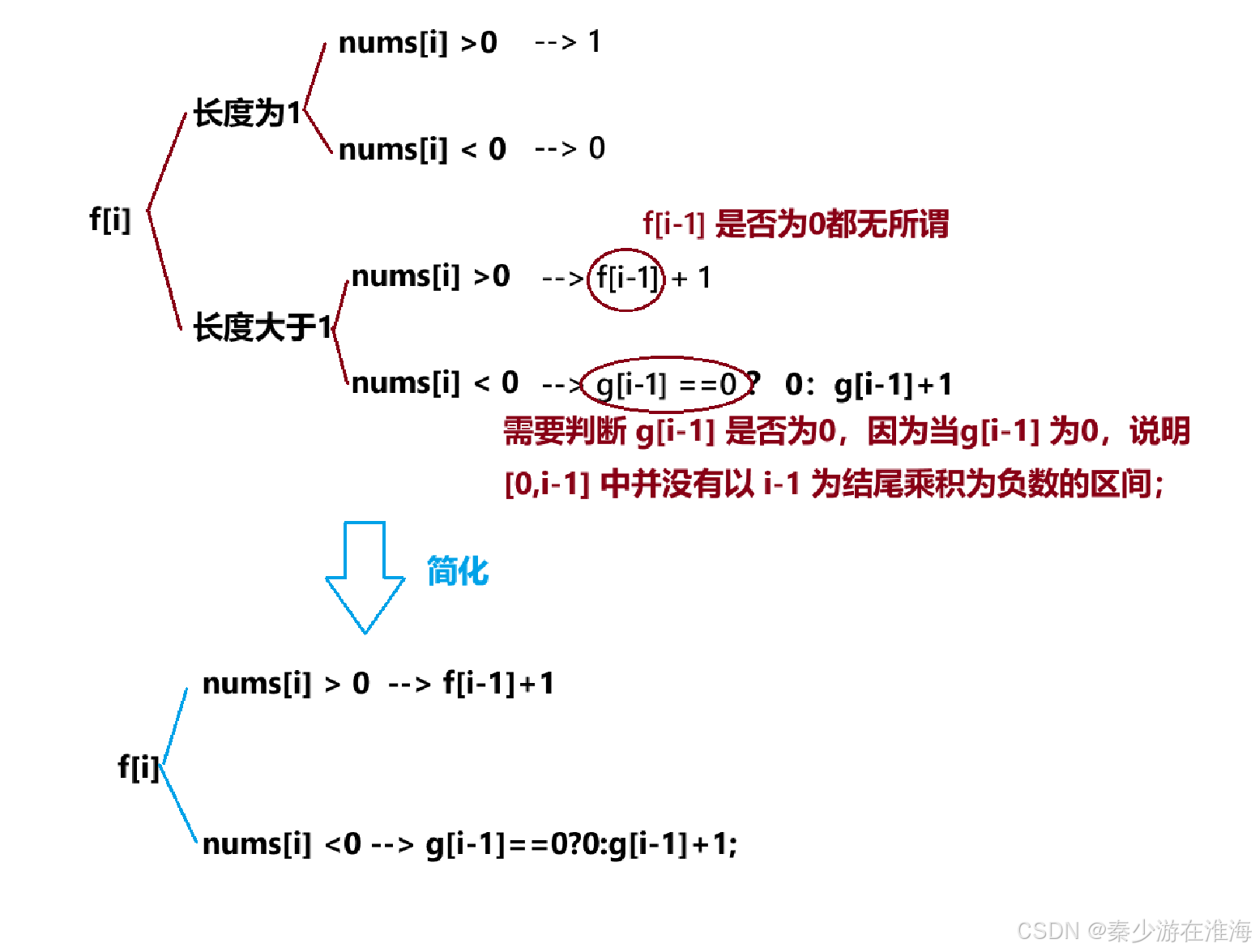
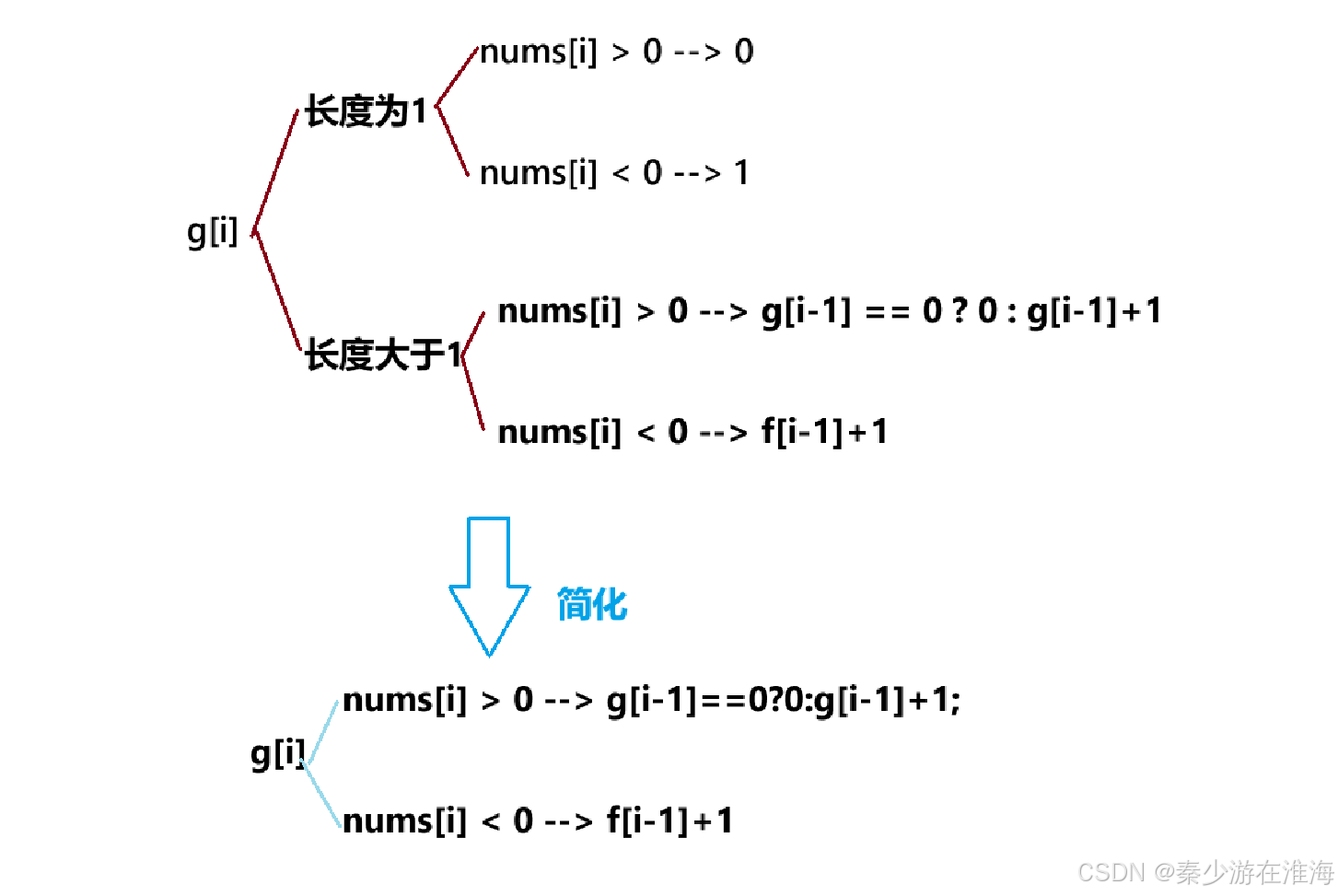
而其中当 nums[i] 为0,0 乘以任何数均为0,两个dp 表会被默认初始化为0,当为0的时候只要不符合上述的情况直接就是0了;
4.3 初始化
观察我们的状态转移方程,当 i 为0 的时候,两个dp表均会发成越界,所以我们需要初始化 f[0]、g[0] ;当 i 为0时,对于 f[0] 意味着以下标为0结尾区间乘积为正数的最大长度,需要判断nums[0] 为正数还是为负数,当nums[0] 为正数,f[0] = 1,当 nums[0] 为负数,f[0] = 0; 对于 g[0] 意味着以下标为0为结尾区间乘积为负数的最大长度,需要判断nums[0] 为正数还是为负数,当nums[0] 为正数,g[0] = 0,当 nums[0] 为负数,g[0] = 1;
当然了,还有一种处理方式,可以为这两个 dp 表多开辟一个空间,但是需要注意虚拟节点中的值需要保证后面填表的正确性以及下标的映射关系;观察状态转移方程,f[0] 应该初始化为 0 , g[0] 应该初始化为0;
4.4 填表顺序
确定填表顺序是为了保证我们填写当前状态时所依赖的状态是已经知道的,观察状态转移方程,当我们填写第 i 个位置的时候,依赖第 i-1 位置上的数据,所以我们的填表顺序为从左往右,并且两个表需要同时填写;
4.5 返回值
返回 f 表中的最大值即可
参考代码1:
int getMaxLen(vector<int>& nums)
{
int n = nums.size();
vector<int> f(n) ,g(n);
//初始化
if(nums[0] <0) f[0] = 0, g[0] = 1;
else if(nums[0] >0) f[0] = 1,g[0] =0;
//填表
int ret = f[0];
for(int i = 1;i<n;i++)
{
//两个表需要同时填写
if(nums[i] <0)
{
f[i] = g[i-1]==0?0:g[i-1]+1;
g[i] = f[i-1]+1;
}
else if(nums[i] >0)
{
f[i] = f[i-1]+1;
g[i] = g[i-1]==0?0:g[i-1]+1;
}
ret = max(ret , f[i]);
}
return ret;
}当然也可以为两个dp 表多开辟一个空间:
参考代码2:
int getMaxLen(vector<int>& nums)
{
int n = nums.size();
vector<int> f(n+1) ,g(n+1);
//填表
int ret = INT_MIN;
for(int i = 1;i<=n;i++)
{
//两个表需要同时填写
if(nums[i-1] < 0)
{
f[i] = (g[i-1]==0 ? 0 : g[i-1]+1);
g[i] = f[i-1]+1;
}
else if(nums[i-1] > 0)
{
f[i] = f[i-1]+1;
g[i] = (g[i-1]==0 ? 0 : g[i-1]+1);
}
ret = max(ret , f[i]);
}
return ret;
}5、题5 等差数列划分:

在正式做本题之前,我们需要了解一些小知识点:

如果 a b c d 构成等差,并且 c d e 也构成等差,那么 a b c d e 也构成等差;
5.1 确定状态表示
状态表示一般是以某一个位置为结尾,或者是以某一个位置为起始;
根据题干以及经验,dp[i] 表示:以 i 位置元素为结尾的所有子数组中有多少个等差数列;
5.2 状态转移方程
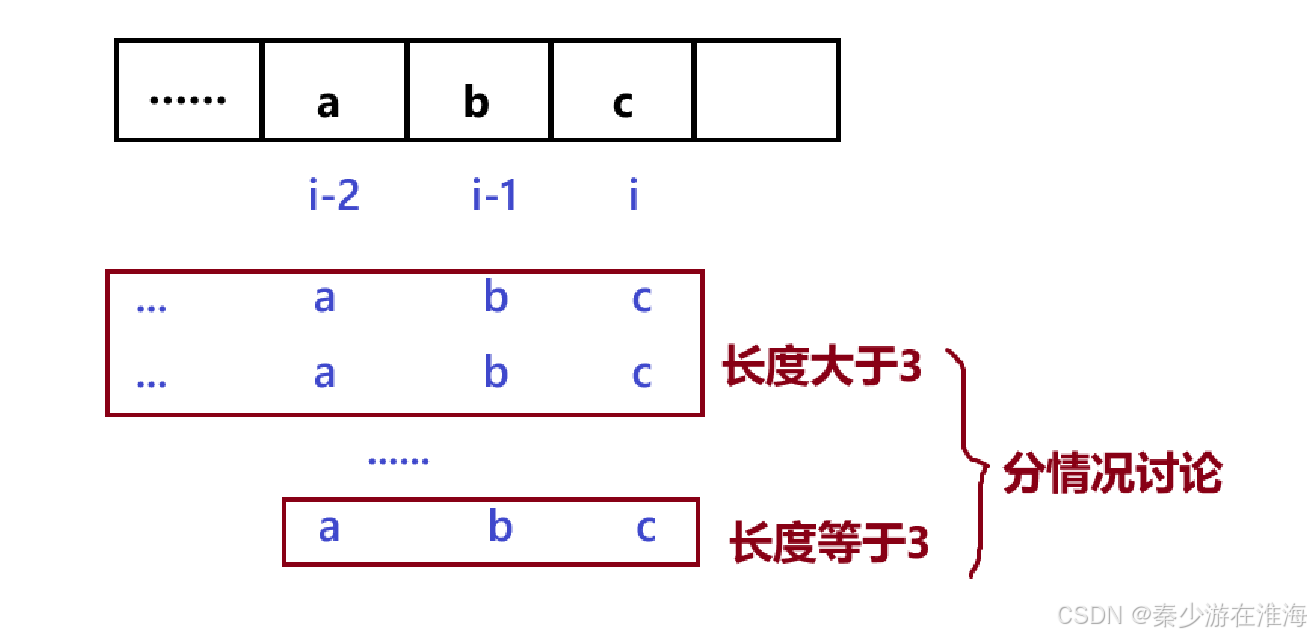
走到 i 位置的时候,看 i-2 与 i-1 位置是否与i 位置构成等差数组;
如果能构成等差,那么 dp[i] = dp[i-1] + 1 ; 加上的1就是当前长度未3的等差子数组;如果不能构成等差数组,那么 dp[i] = 0;
即 dp[i] = c-b == b-1 ? dp[i-1]+1:0;
5.3 初始化
观察我们的状态转移方程就可以发现,当 i 为0的时候,下标不合法,我们就需要初始化 dp[0];当 i 为0 的时候,该数组中只有一个元素,长度不符合构成等差子数组的条件,dp[0] = 0; 同理,下标为1 的子数组也长度也不符合构成等差子数组的条件,故而 dp[1] = 0;
5.4 填表顺序
从左往右
5.5 返回值
将 dp 表中的所有数据相加然后返回
参考代码:
int numberOfArithmeticSlices(vector<int>& nums)
{
int n = nums.size();
if(n==1 || n==2) return 0;
vector<int> dp(n);
//初始化
dp[0] = dp[1] = 0;
//填表
int ret = 0;
for(int i =2;i<n;i++)
{
dp[i] = ((nums[i]-nums[i-1])==(nums[i-1]-nums[i-2]) ? dp[i-1]+1:0);
ret += dp[i];
}
return ret;
}6、题6 最长湍流子数组:

题干中“湍流”的意思大概是这样子:
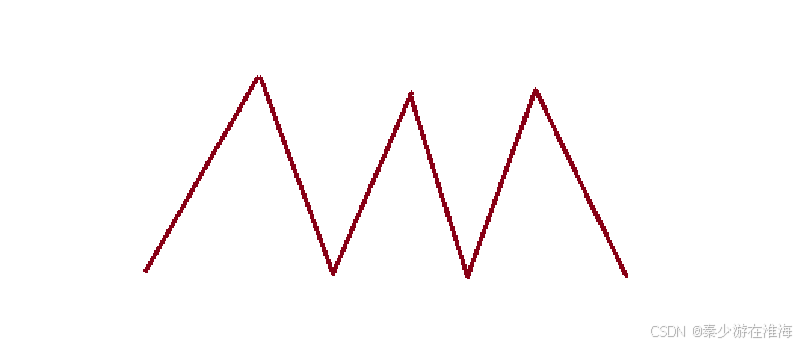
也就是当前这个数小于前一个数的话,那么也小于其后一个数;
6.1 确定状态表示
状态表示一般是以某一个位置为结尾,或者是以某一个位置为起始;
根据题干以及经验,dp[i] 表示:以 i 位置元素为结尾的所有子数组中,最长的湍流数组的长度;
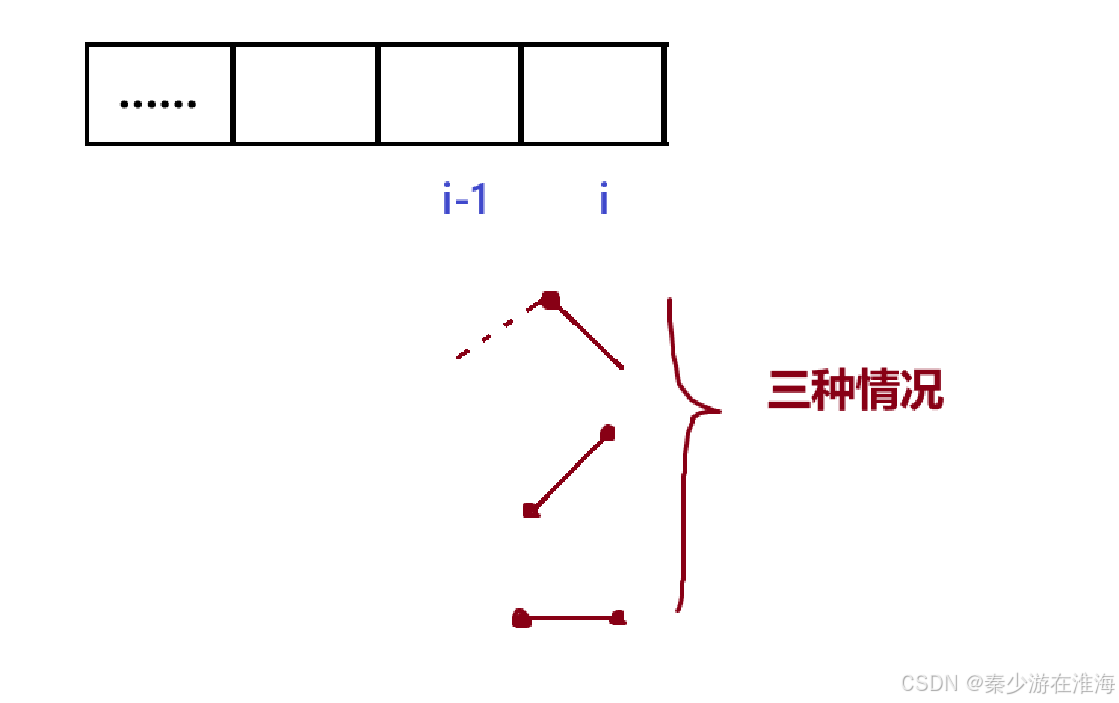
但是,最后一个状态有多种情况:下降、上升、不变;
显然一个dp 表是不够的,我们至少需要使用两个 dp 表来表示:
f[i] 表示: 以 i 位置为结束的所有子数组中,最后呈现“上升”状态下的最长湍流子数组的长度
g[i] 表示: 以 i 位置为结束的所有子数组中,最后呈现“下降”状态下的最长湍流子数组的长度
6.2 状态转移方程
对于 f[i] 来说,需要分三种情况讨论;当 nums[i] > nums[i-1], “下降状态” ,f[i] = 1 ; 当 nums[i]<nums[i-1] , 此时从 i-1 到 i 处是短暂的“上升”状态,想求得其湍流的最大长度,即从 i-2 到 i-1 是下降趋势,即g[i-1] ,所以 f[i] = g[i-1] +1; 当 nums[i] == nums[i-1] , f[i] = 1;
对于g[i] 来说,也需要分为三种情况进行讨论;当 nums[i] > nums[i-1] , 此时从 i-1 到 i 处是短暂“下降”状态,想求得其湍流的最大长度,即从 i-2 到 i-1 是上升趋势,即f[i-1] ,所以 g[i] = f[i-1] +1; 当 nums[i]<nums[i-1] , "上升"状态,不符合g[i] 最后呈现“下降”状态,所以 g[i] = 1;当 nums[i] == nums[i-1] , g[i] = 1;

6.3 初始化
观察我们的状态转移方程,当 i 为0 的时候,两个dp表均会发成越界,所以我们需要初始化 f[0]、g[0] ;实际上可以将f、g 表中的数据全部初始化为1,那么在填表的时候就只需要考虑两种情况;
6.4 填表顺序
从左往右,两个表一起填写;
6.5 返回值
返回两个表中的最大值即可;
参考代码:
int maxTurbulenceSize(vector<int>& arr)
{
int n = arr.size();
vector<int> f(n,1),g(n,1);
//填表
int ret = 1;
for(int i = 1;i<n;i++)
{
if(arr[i-1] > arr[i]) g[i] = f[i-1] +1;//降序
else if(arr[i-1] < arr[i]) f[i] = g[i-1] +1;//升序
ret = max(ret , max(f[i] , g[i]));
}
return ret;
}7、题7 单词拆分:
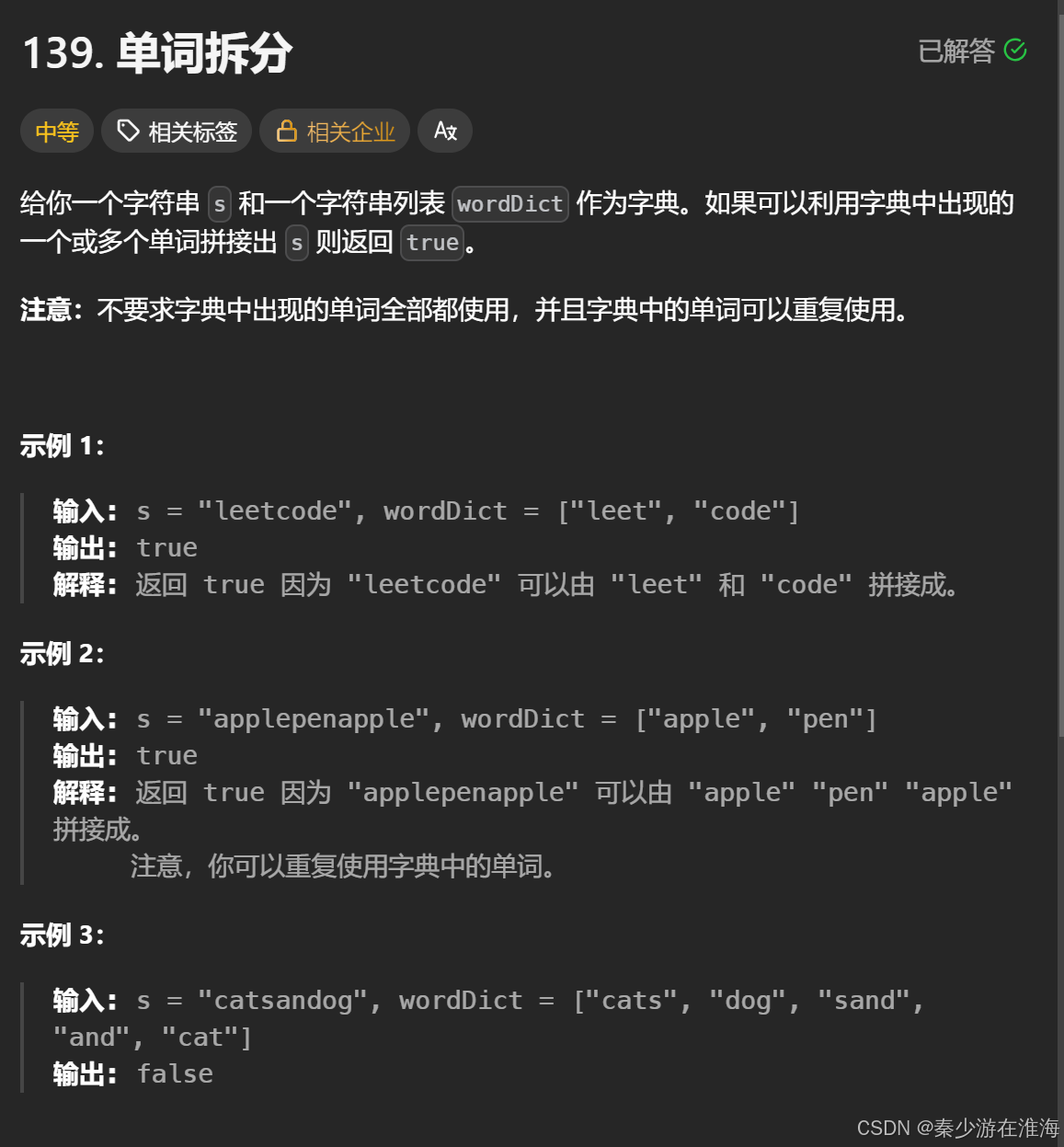
7.1 确定状态表示
dp[i] 表示: [0,i] 区间内的字符串,能否被字典中的单词拼接而成;能的话存放true,不能则存放false;
最后一个位置相当于最后一个单词;要么最后一个字符构成一个单词,要么最后两个字符构成一个单词,要么最后三个字符构成一个单词……
将字符串划分为两部分:前面部分+自己当前的这个单词
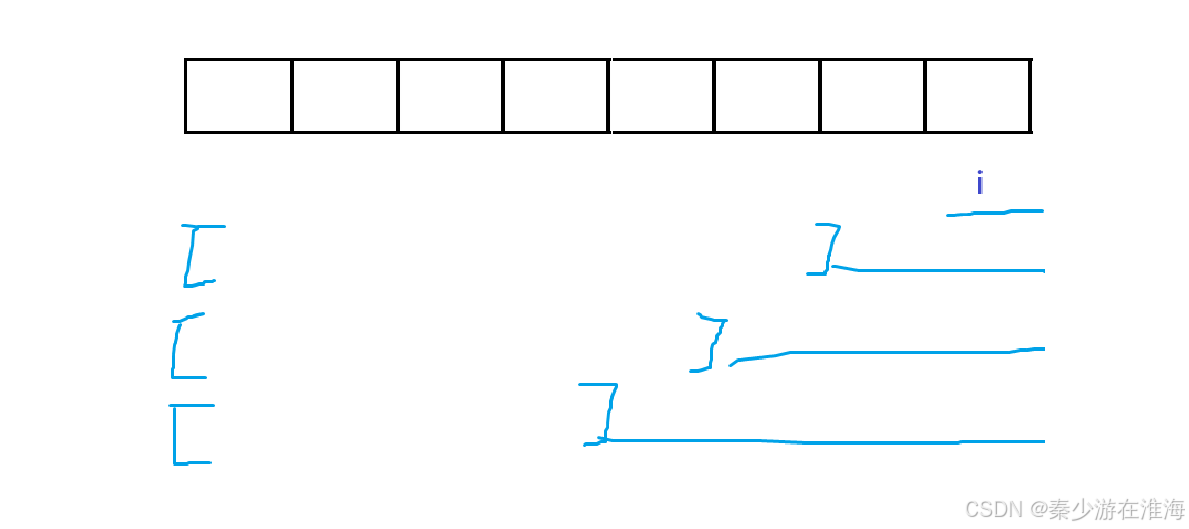
只要能确定前面部分的字符串能够被拼接而成,并且最后的这个单词在字典中,那么整个字符串就可以被拼接而成了;
7.2 状态转移方程
根据最后一个状态来划分问题,假设 j 为最后一个单词的起始下标;

7.3 初始化
此处我们为dp 表多开辟一个空间;需要注意,虚拟节点中的值要保证后面填表的正确性,以及下标的映射关系;
dp[0] 应该初始化为 true;
还有一个小技巧:可以在字符串前面随便增加一个字符,这样在填表的时候就不用处理下标的映射关系了;很多字符串的问题都涉及找子串的这一步,如果不这样处理,在找子串处理下标映射的过程之中就会非常麻烦;
7.4 填表顺序
从左往右;
7.5 返回值
返回dp[n] ,只要[0,n]可以用字典中的单词拼接构成,那么该字符串s 就可以用字典中的单词拼接构成;
参考代码:
bool wordBreak(string s, vector<string>& wordDict)
{
//优化,将单词放入hash中,加快查找
unordered_set<string> hash;
for(auto& s : wordDict) hash.insert(s);
int n = s.size();
vector<bool> dp(n+1 , false);//初始化为false,在填表的时候就可以少判断
//初始化
dp[0] = true;
//下标的映射处理
s = ' ' +s;//小技巧
for(int i = 1;i<=n;i++)//区间 [0,i]
{
for(int j = i;j>=1;j--)//最后一个单词的起始位置
{
//填表
if(dp[j-1]==true && hash.count(s.substr(j,i-j+1)))
{
dp[i] = true;
break;
}
}
}
return dp[n];
}8、题8 环绕字符串中唯一的子字符串 :
467. 环绕字符串中唯一的子字符串 - 力扣(LeetCode)
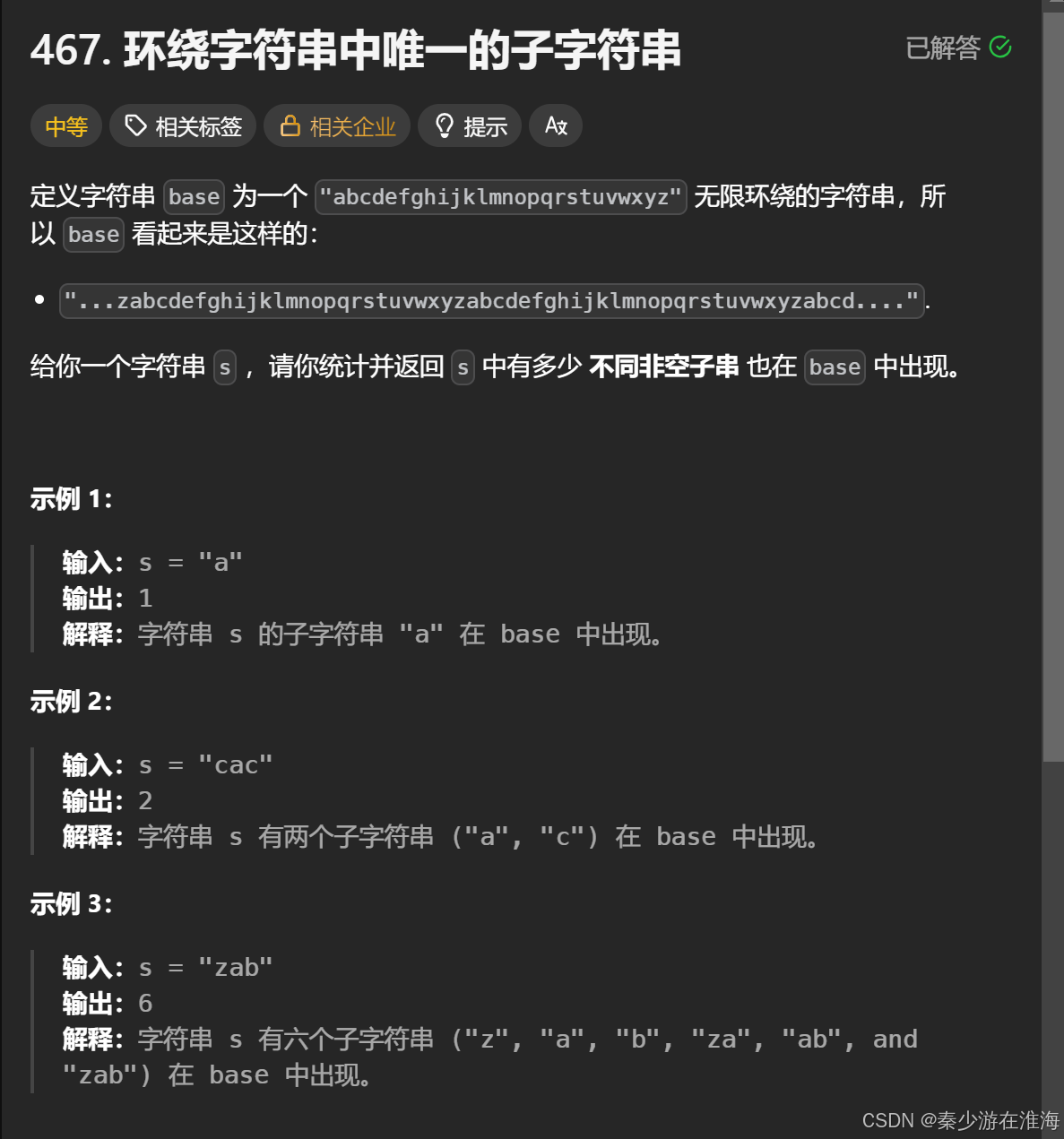
8.1 确定状态表示
根据我们的经验以及题干要求;
dp[i] 表示:以 i 位置的元素为结尾的所有子串中,有多少个在base中出现过;
8.2 状态转移方程
同样我们可以划分为两种情况 :长度为1,以及长度大于1;
对于dp 来说,当长度为1的时候,一定能在base 中找到,即dp[i] =1; 而长度大于1,就需要判断它们之间是否是连续的:有可能是递增也有可能是从'z' 到 ‘a' ,即 s[i-1] == s[i] +1 || (s[i-1] == 'z' && s[i] =='a' ) 那么dp[i] 等于dp[i-1];
8.3 初始化
观察我们的状态转移方程,将dp表全部初始化为1,那么在填表的时候就可以少判断;
8.4 填表顺序
从左往右
8.5 返回值
此处不能直接返回dp 表中所有值的和;
需要进行去重处理:当相同字符结尾的dp 值,我们取最大即可,因为大值中包含了小值;
创建一个大小为26的数组,里面的值保存相应字符结尾的最大的dp 值即可;
参考代码:
int findSubstringInWraproundString(string s)
{
int n = s.size();
vector<int> dp(n,1);
//填表
for(int i = 1;i<n;i++)
{
if(s[i-1]+1==s[i] ||(s[i-1]=='z' && s[i] == 'a')) dp[i] = dp[i-1] + 1;
}
//去重处理
int hash[26] = {0};
for(int i = 0;i<n;i++)
{
hash[s[i] - 'a'] = max(dp[i] , hash[s[i] - 'a']);
}
int sum = 0;
for(auto e:hash) sum+=e;
return sum;
}总结
动态规划五个步骤:
- 1、确定一个动态表达式
- 2、根据该动态表达式来推导状态转移方程
- 3、初始化
- 4、填表顺序
- 5、返回值
一般有三种方式可以来确定状态表示:
- 1、题目怎么要求,我们就怎么定义状态表示
- 2、经验 + 题目要求
- 3、分析题目的过程中发现重复的子问题(再将重复的子问题抽象为状态表达式)
推导状态转移方程:1、用之前或者之后的状态推导得到dp[i] 的值 ; 2、根据最近的一步来划分问题;
初始化的目的:保证填dp表(根据状态转移方程来调表)的时候不会发生越界;
填表顺序的目的是为了保证在填表的时候,所要依据的状态已经存在了;





















 763
763

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








